
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальные оценки для генеральной среднейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При выборке малого объема точечная оценка может сильно отличаться от оцениваемого параметра, поэтому широко используют интервальные оценки. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Доверительной вероятностью (надежностью) называется вероятность g, с которой осуществляется неравенство
Интервальные оценки для генеральной средней с известным s
Пусть известно среднее квадратическое отклонение s генеральной совокупности с нормальным законом распределения. Требуется оценить неизвестное математическое ожидание а по выборочной средней Тогда по следствию интегральной теоремы Лапласа имеем: Число Пример. Случайная величина Найдем t: функция Лапласа
Интервальная оценка для генеральной средней с неизвестным s
Пусть признак Х генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s неизвестно. Требуется оценить неизвестное математическое ожидание а по выборочной средней Пример. Средняя урожайность пшеницы на 16 опытных участках Число степеней свободы
Интервальные оценки для генеральной дисперсии, среднего квадратического отклонения и генеральной доли Пусть из генеральной совокупности, распределенной по нормальному закону Случайная величина По таблице
Тогда:
Если Можно по упрощенной формуле (Гмурман): Пример. По результатам контроля n = 9 деталей вычислено
По таблице
Интервальная оценка для генеральной доли
Пусть в n независимых испытаниях событие А, вероятность появления которого равна р, имело место m раз ( Пример. При испытании зерна на всхожесть из 400 зерен проросло 384. С надежностью g = 0,98 определить доверительный интервал для генеральной доли р.
Глава 24. Статистическая проверка статистических гипотез
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

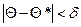 , т.е.
, т.е. 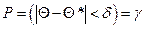 , где Q* – найденная характеристика параметра Q. Надежность g обычно выбирается 0,95; 0,99; 0,999 и т.д.
, где Q* – найденная характеристика параметра Q. Надежность g обычно выбирается 0,95; 0,99; 0,999 и т.д.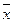 . Будем рассматривать выборочную среднюю
. Будем рассматривать выборочную среднюю 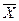 , для которой
, для которой 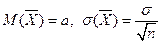 (
( , где
, где 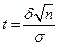 ,
, 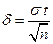 – точность оценки.
– точность оценки.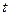 определяем по таблице значений функции Лапласа:
определяем по таблице значений функции Лапласа: 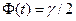 . Получаем:
. Получаем: 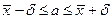 ,
, 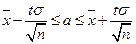 – интервальная оценка для математического ожидания а.
– интервальная оценка для математического ожидания а.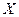 имеет нормальное распределение с s =3. Найти доверительный интервал для оценки генеральной средней а, если
имеет нормальное распределение с s =3. Найти доверительный интервал для оценки генеральной средней а, если 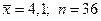 , надежность g = 0,95.
, надежность g = 0,95.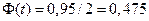 ,
, 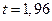 , точность:
, точность: 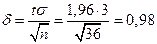 ,
, 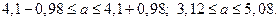
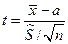 , имеющая распределение Стьюдента с числом степеней свободы
, имеющая распределение Стьюдента с числом степеней свободы 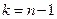 . Получаем:
. Получаем: 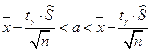 где n – объем выборки,
где n – объем выборки, 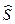 –исправленное среднее квадратическое отклонение,
–исправленное среднее квадратическое отклонение,  – выборочная средняя,
– выборочная средняя, 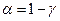 – уровень значимости,
– уровень значимости, 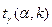 находим по распределению Стьюдента (t – распределение) (для двухсторонней критической области). Точность оценки:
находим по распределению Стьюдента (t – распределение) (для двухсторонней критической области). Точность оценки:  . Можно по таблице приложения 3 Гмурмана.
. Можно по таблице приложения 3 Гмурмана.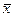 =25 ц/га, а
=25 ц/га, а 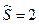 ц/га. Найти с надежностью 0,9 границы доверительного интервала для оценки генеральной средней.
ц/га. Найти с надежностью 0,9 границы доверительного интервала для оценки генеральной средней.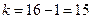 ,
, 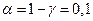 , по таблице распределения Стьюдента находим:
, по таблице распределения Стьюдента находим: 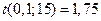 . Точность оценки:
. Точность оценки: 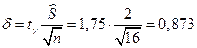 ; тогда
; тогда 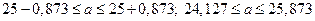 (ц/га).
(ц/га).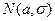 , взята выборка объема n и вычислена исправленная выборочная дисперсия
, взята выборка объема n и вычислена исправленная выборочная дисперсия  . Требуется определить с надежностью g интервальные оценки для s 2 и s.
. Требуется определить с надежностью g интервальные оценки для s 2 и s.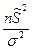 имеет распределение Пирсона (
имеет распределение Пирсона (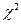 )с
)с 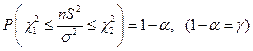 .
.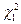 и
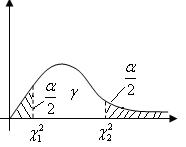
и  , чтобы площадь, заключенная под графиком плотности распределения
, чтобы площадь, заключенная под графиком плотности распределения 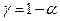 . Обычно:
. Обычно: 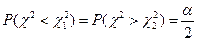 .
.
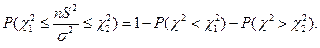 Поскольку таблица содержит лишь
Поскольку таблица содержит лишь 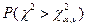 , то
, то 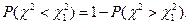 тогда из
тогда из 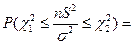
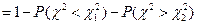 :
: 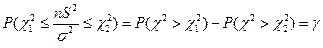 , т.е.
, т.е. 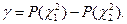 Эта формула используется при решении обратной задачи – нахождение доверительной вероятности по заданному доверительному интервалу генеральной дисперсии.
Эта формула используется при решении обратной задачи – нахождение доверительной вероятности по заданному доверительному интервалу генеральной дисперсии.  Запишем неравенство из
Запишем неравенство из 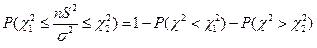 :
: 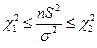 и преобразуем его:
и преобразуем его:  .
.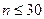 , то доверительный интервал для s:
, то доверительный интервал для s: 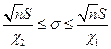 . Если
. Если 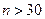 , то
, то 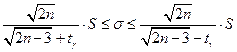 , где
, где 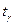 определяется по таблице функции Лапласа:
определяется по таблице функции Лапласа: 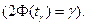
 , где параметр
, где параметр 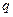 находят по таблице приложения 4 (Гмурман) по заданным n и g.
находят по таблице приложения 4 (Гмурман) по заданным n и g.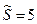 мм. В предположении, что ошибка распределена нормально, определить при g = 0,95 доверительный интервал для s.
мм. В предположении, что ошибка распределена нормально, определить при g = 0,95 доверительный интервал для s.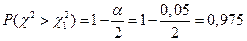 ;
; 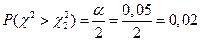 .
. ,
, 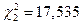 ,
,  (мм).
(мм).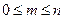 ), тогда границы доверительного интервала для генеральной доли:
), тогда границы доверительного интервала для генеральной доли:  , где
, где  ,
,  (Лаплас),
(Лаплас), 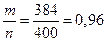 , точность оценки:
, точность оценки: 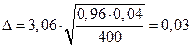 ;
; 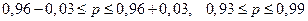 .
.


