
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность и надежность оценки. Доверительные интервалыСодержание книги
Поиск на нашем сайте
Как уже было сказано выше, точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, - точечные. При выборке малого объёма точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объёме выборки следует пользоваться интервальными оценками. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надёжность оценок (смысл этих понятий выясняется ниже). Пусть найденная по данным выборки статистическая характеристика Однако статистические методы не позволяют категорически утверждать, что оценка Надёжностью (доверительной вероятностью) оценки Пусть вероятность того, что Заменив неравенство
Это соотношение следует понимать так: вероятность того, что интервал Замечание. Интервал Так как случайной величиной является не оцениваемый параметр Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера. Доверительные интервалы для оценки математического ожидания нормального распределения при известном Пусть количественный признак Х генеральной совокупности распределён нормально, причём среднее квадратическое отклонение Примем без доказательства, что если случайная величина Х распределена нормально, то выборочная средняя
Приняв во внимание, что по условию нам задана вероятность
Смысл полученного соотношения таков: с надёжностью Укажем ещё, что число t определяется из равенства Поясним смысл, который имеет заданная надёжность. Надёжность Доверительным вероятностям, как это видно из таблицы функции Лапласа, соответствуют следующие величины нормированных отклонений: вероятности вероятности вероятности Выбор того или иного порога доверительной вероятности исследователь осуществляет исходя из практических соображений той ответственности, с какой делаются выводы о генеральных параметрах.
Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном Пусть количественный признак Х генеральной совокупности распределён нормально, причём среднее квадратическое отклонение Оказывается, что по данным выборки можно построить случайную величину Пользуясь распределением Стьюдента, находим:
Значит, доверительный интервал Пример. Случайная величина Х – вес полугодовалого поросенка в хозяйстве (то есть в генеральной совокупности) - распределена нормально. По выборке объёма n = 16 найдены выборочная средняя Решение. Найдём Найдём доверительные границы:
Итак, с надёжностью 0,95 неизвестный параметр Доверительные интервалы для оценки среднего квадратического отклонения Пусть количественный признак Х генеральной совокупности распределён нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение Доверительный интервал, покрывающий параметр
Здесь параметр q определяют, пользуются таблицей приложения 2, а S находят по выборке. Пример. Случайная величина Х – вес полугодовалого поросенка в хозяйстве – (то есть в генеральной совокупности) распределён нормально. По выборке объёма n=25 найдено «исправленное» среднее квадратическое отклонение S=0,8 кг. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение Решение. По таблице приложения 2 по данным Искомый доверительный интервал таков: 0,8 (1 - 0,32)< 0,544< Замечание. Если q>1, то неравенство примет вид 0< 7. Статистические гипотезы. Статистические критерии
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.149 (0.007 с.) |

 служит оценкой неизвестного параметра
служит оценкой неизвестного параметра 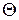 . Будем считать
. Будем считать 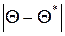 .
.  Другими словами, если
Другими словами, если 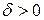 и
и 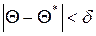 , то чем меньше
, то чем меньше 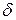 , тем оценка точнее. Таким образом, положительное число
, тем оценка точнее. Таким образом, положительное число 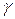 , с которой это неравенство осуществляется.
, с которой это неравенство осуществляется.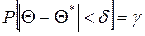 .
.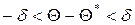 , или
, или  , имеем
, имеем 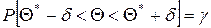 .
.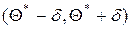 заключает в себе (покрывает) неизвестный параметр
заключает в себе (покрывает) неизвестный параметр 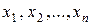 .
.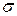 .
.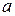 по выборочной средней
по выборочной средней 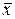 . Поставим своей задачей найти доверительные интервалы, покрывающие параметр
. Поставим своей задачей найти доверительные интервалы, покрывающие параметр  , найденная по независимым наблюдениям, также распределена нормально. Параметры распределения
, найденная по независимым наблюдениям, также распределена нормально. Параметры распределения 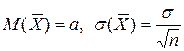 .
. .
. покрывает неизвестный параметр
покрывает неизвестный параметр 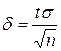 .
.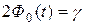 , или
, или 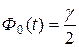 ; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа, равное
; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа, равное 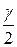 .
.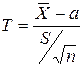 , которая имеет распределение Стьюдента с k = n-1 степенями свободы; здесь
, которая имеет распределение Стьюдента с k = n-1 степенями свободы; здесь 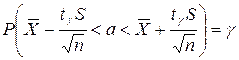 .
.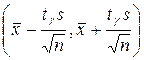 покрывает неизвестный параметр
покрывает неизвестный параметр 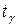 .
.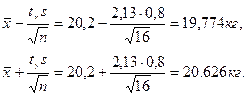
 .
.


