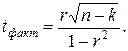Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционная зависимость. Коэффициент корреляции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Зависимость между значениями одной случайной величины и условным средним значением другой случайной величины носит название корреляционной (от англ. correlation - согласование, связь, взаимосвязь, соотношение, взаимозависимость); термин впервые введен Гальтоном в 1888г. Парный коэффициент корреляции Пирсона (1896 г.) изменяется в пределах от -1 до +1. Значение 0,00 интерпретируется как отсутствие корреляции. Корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу. Рабочие формулы коэффициентов корреляции применяют с учетом того, с какой выборкой (большей или малой) мы имеем дело. Например, для малых выборок удобнее всего пользоваться следующей формулой:
у-варианты второго признака; n-число наблюдений в выборке. Вспомогательная таблица для расчетов коэффициента корреляции.
Коэффициент корреляции, возведенный в квадрат, называется коэффициентом детерминации r2. Он показывает долю изменений, которые вызваны факторным признаком. Коэффициент детерминации r2 является прямым способом выражения зависимости одного признака от другого. Если известно, что У находится в причинной связи с Х, то r2 – это доля вариации У, обусловленная влиянием Х. Для изучения корреляционных связей большое значение имеет коэффициент регрессии Формула для расчета коэффициента имеет вид:
Корреляционные зависимости наблюдаются между очень многими признаками организмов – морфологическими, физиологическими, а также между различными биологическими процессами. Различают положительную и отрицательную корреляции. При положительной корреляции с увеличением одного признака увеличивается и другой. Например, с увеличением живой массы коров первотёлок возрастает и удой; чем выше процент жира в молоке, тем выше и процент белка в нём. При отрицательной корреляции с увеличением удоя у коров снижается жирность молока; куры с высокой яйценоскостью имеют более мелкие яйца.
В зоотехнической и ветеринарной практике изучение корреляционной зависимости имеет большое значение. Так, например, для животновода очень важно знать, какова связь между средним удоем за лактацию и процентом жира в молоке, иначе говоря, дают ли более высокоудойные коровы молоко с повышенным содержанием жира или, наоборот, с пониженным и насколько часто встречаются исключения из той или другой зависимости. Или другой пример: из-за отрицательной корреляционной зависимости между высокой молочностью и способностью к откорму невозможно выведение породы, сочетающую высокую молочную продуктивность и высокие мясные качества; между устойчивостью к эймериозу у кур и массой тела существует положительная корреляция, поэтому, чем более упитанные куры, тем менее они предрасположены к заболеванию.
Надежность зависимости. Определяют две черты зависимости между переменными: величину зависимости и надежность зависимости. Надежность зависимости – менее наглядное понятие, чем величина зависимости, однако чрезвычайно важна. Оно непосредственно связано с репрезентативностью той определенной выборки, на основе которой строятся выводы. Другими словами, надежность говорит, насколько вероятно, что зависимость подобная найденной, будет вновь обнаружена (подтвердится) на данных другой выборки, извлеченной из той же самой популяции. Если исследование удовлетворяет некоторым специальным критериям, то надежность найденных зависимостей между переменными выборки можно количественно оценить и представить с помощью стандартной статистической меры (называемой р-уровень, или статистический уровень значимости). Статистическая значимость результата представляет собой оцененную меру уверенности в его правильности. Уровень значимости или р-уровень, - это показатель, находящийся в убывающей зависимости от надежности результата. Более высокий р-уровень соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно р-уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию. Чем слабее зависимость между переменными, тем большего объема требуется выборка, чтобы значимо ее обнаружить. Другими словами, если зависимость между переменными почти отсутствует, объем выборки, необходимый для ее значимого обнаружения, почти равен объему всей популяции, которой предполагается бесконечным.
Так как надежность изучения связей в значительной степени зависит от количества сопоставляемых данных, необходимо измерять существенность полученного уравнения регрессии и индекса (коэффициента) корреляции. Показатели корреляции, исчисленные для ограниченной по объему совокупности, могут быть искажены действием случайных факторов. Существенность индекса (коэффициента) корреляции, а, следовательно, всего уравнения регрессии, может быть оценена с помощью дисперсионного анализа (F -критерия Фишера). При этом сравнивают факторную и остаточную дисперсии с учетом числа степеней свободы вариации. F -критерий в данном случае рассчитывают по формуле:
где
n – численность выборочной совокупности; k – число параметров в уравнении регрессии. Значение F -критерия можно получить также, используя значения индекса или коэффициента корреляции:
Полученное значение F-критерия сравнивают с табличным значением. При этом для факторной дисперсии число степеней свободы вариации составляет Для оценки значимости индекса (коэффициента) корреляции и уравнения регрессии также используют t -критерий Стьюдента, который для больших выборок рассчитывают по формулам:
Для малых выборок формулы имеют вид:
Также, как при дисперсионном анализе, фактическое значение t -критерия сравнивают с табличным с учетом числа степеней свободы вариации n = n - k. Если фактическое значение t-критерия больше табличного, то связь достоверна, если меньше, то связь несущественна.
Рассмотрим методику корреляционного анализа для парной корреляции. Пример. По выборочным данным получены сведения о среднегодовом удое коров и расходе кормов на голову (табл. 14). Т а б л и ц а 14
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.170.253 (0.012 с.) |

 (или
(или 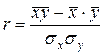 ), где
), где и
и  , где х-варианты первого признака;
, где х-варианты первого признака; =
=
 , который показывает, насколько в среднем изменяется признак (Х), если коррелирующий с ним признак (У) изменяется на определенную величину.
, который показывает, насколько в среднем изменяется признак (Х), если коррелирующий с ним признак (У) изменяется на определенную величину. ;
; 
 ,
, - выборочная факторная дисперсия;
- выборочная факторная дисперсия; - выборочная остаточная дисперсия;
- выборочная остаточная дисперсия;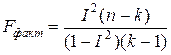 ;
;  .
. , а для остаточной дисперсии
, а для остаточной дисперсии  Если фактическое значение F-критерия больше табличного, следовательно, связь между признаками достоверна и уравнение регрессии в полной мере отражает эту связь. Если фактическое значение F-критерия меньше табличного, то можно сделать вывод, что связь между признаками носит случайный характер.
Если фактическое значение F-критерия больше табличного, следовательно, связь между признаками достоверна и уравнение регрессии в полной мере отражает эту связь. Если фактическое значение F-критерия меньше табличного, то можно сделать вывод, что связь между признаками носит случайный характер.