
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однофакторный дисперсионный анализ.Содержание книги
Поиск на нашем сайте
Предположим, что имеется Подобная ситуация возникает, когда существует некий фактор, принимающий Предполагается, что ошибки нормально распределены: Основной гипотезой, нуждающейся в проверке, является гипотеза о равенстве групповых средних Рассмотрим группу экспериментальных животных, подвергнутых ультрафиолетовому облучению. В процессе эксперимента измерялась температура тела животных. Результаты измерений были занесены в таблицу:
Таблица 11 Температура тела животных
Физический фактор А (ультрафиолетовое излучение) имеет В данном эксперименте число проведенных наблюдений при действии каждого из уровней фактора одинаково. Все значения величины Х, наблюдаемые при каждом фиксированном уровне фактора Аj, составляют группу, и в последней строке таблицы представлены соответствующие выборочные групповые средние, вычисленные по формуле
Здесь n – число испытаний,
Введем следующие понятия: Факторная сумма квадратов отклонений групповых средних от общей средней
Остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней
Общая сумма квадратов отклонений наблюдаемых значений от общей средней
Можно доказать следующее равенство:
С помощью
В основе однофакторного дисперсионного анализа лежит тесная связь между различием в групповых средних Для сравнения двух дисперсий используют показатель критерия Фишера При этом при заданном уровне значимости проверяют нулевую гипотезу о равенстве факторной и остаточной дисперсии (изучаемый фактор не вызывает изменчивости признака) при конкурирующей гипотезе об их неравенстве (изучаемый фактор вызывает изменчивость признака). По таблице критических значений распределения Фишера-Снедекора при уровне значимости, равном половине заданного уровня Замечание. Если окажется, что Если проверка покажет значимость различий между
Пример. Имеются данные о настриге шерсти овец в зависимости от их живой массы (табл. 12). Т а б л и ц а 12 Настриг шерсти овец, кг
Требуется определить достоверность разницы в настриге шерсти овец в зависимости от их живой массы с уровнем вероятности суждения 0,05. Для расчета показателей вариации настриг шерсти овец возведем в квадрат (табл. 13). Т а б л и ц а 13
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.108.150 (0.006 с.) |

 выборок с объемами
выборок с объемами 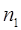 ,
,  ,
,  , и наблюдения можно представить в виде
, и наблюдения можно представить в виде 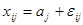 , где
, где 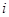 - номер наблюдения в выборке;
- номер наблюдения в выборке;  - номер выборки;
- номер выборки;  - групповые математические ожидания;
- групповые математические ожидания; 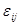 - случайные ошибки с
- случайные ошибки с  =0, о которых предполагается, что они независимы и одинаково расположены.
=0, о которых предполагается, что они независимы и одинаково расположены. . Тогда можно изучать влияние фактора, вычисляя дисперсии некоторых величин. Совокупность этих методов называют однофакторным дисперсионным анализом.
. Тогда можно изучать влияние фактора, вычисляя дисперсии некоторых величин. Совокупность этих методов называют однофакторным дисперсионным анализом. . Иными словами, проверяют гипотезу о том, что фактор вообще не влияет на наблюдения. В случае нормальных ошибок ее можно проверить, вычислив две разные оценки дисперсии.
. Иными словами, проверяют гипотезу о том, что фактор вообще не влияет на наблюдения. В случае нормальных ошибок ее можно проверить, вычислив две разные оценки дисперсии.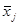
 постоянных уровней (3 различных мощности облучения). На всех уровнях распределения случайной величины Х (температуры тела животного) предполагается нормальным, а дисперсии одинаковыми, хотя и неизвестными.
постоянных уровней (3 различных мощности облучения). На всех уровнях распределения случайной величины Х (температуры тела животного) предполагается нормальным, а дисперсии одинаковыми, хотя и неизвестными. .
.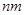 наблюдений находится как
наблюдений находится как .
.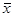 , которая характеризует рассеивание «между группами» (т.е. рассеивание за счет исследуемого фактора):
, которая характеризует рассеивание «между группами» (т.е. рассеивание за счет исследуемого фактора):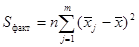 ,
,
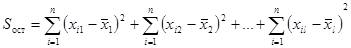 .
.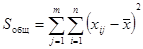 ,
,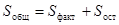 .
. ,
, 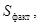
 производится оценка общей, факторной и остаточной дисперсий:
производится оценка общей, факторной и остаточной дисперсий: ,
,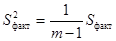 ,
, .
. .
. , находят критическое значение
, находят критическое значение  . Здесь
. Здесь 
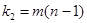 . Если
. Если  , нулевую гипотезу считают согласующейся с результатами наблюдений. Если
, нулевую гипотезу считают согласующейся с результатами наблюдений. Если  , то эту гипотезу отвергают в пользу конкурирующей.
, то эту гипотезу отвергают в пользу конкурирующей. , следует сделать вывод об отсутствии влияния фактора А на Х.
, следует сделать вывод об отсутствии влияния фактора А на Х.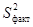 и
и  ,следует сделать вывод о существенном влиянии фактора А на Х.
,следует сделать вывод о существенном влиянии фактора А на Х.



 = 130,1
= 130,1
 = N =
= 20
= N =
= 20
 =
= 848,38
=
= 848,38



