
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ошибка разности между средними арифметическими двух вариационных рядов.Содержание книги
Поиск на нашем сайте
В экспериментальной и практической работе большое значение имеет определение разности между средними показателями двух сравниваемых групп животных и установление достоверности этой разности. Например, часто требуется определить, достоверна ли прибавка удоя при введении в рацион коров какого-либо кормового компонента. В ветеринарных исследованиях очень важно бывает доказать, что примененная доза или новый лекарственный препарат достоверно уменьшает долю заболевших животных по сравнению с долей больных животных в контрольной группе, не подвергавшихся лечению. Определение достоверности разности между средними арифметическими или долями двух вариационных рядов можно определить с помощью ошибки разности md Формула ошибки разности следующая: где Эта формула используется в тех случаях, когда варианты одной выборки некоррелированы с вариантами другой выборки. Критерий достоверности разности между средними арифметическими вычисляют по следующей формуле
Найденный критерий td сравнивают с табличным значением критерия Стъюдента при числе степеней свободы k=n1+n2-2, где n1 и n2 — объемы выборок. Если td< tst - разность считается недостоверной. Это значит, что не получено никакого определённого ответа о разности между соответствующими генеральными параметрами. Если получена благоприятная по смыслу исследования разность между двумя выборочными средними, но эта разность оказалась недостоверной, то это значит, что между соответствующими генеральными средними могут быть любые соотношения, а какие именно неизвестно, но это не может служить доказательством отсутствия разницы между генеральными средними. Если в выборочном исследовании оказалась достоверная разница между выборочными показателями, то такая же разница по знаку будет и между соответствующими генеральными параметрами. Основной вывод может быть перенесён на генеральную совокупность. Для коррелированных выборок используется следующая формула разности между средними: где s1 и s2 – ошибки средних арифметических по каждой выборке;
r – коэффициент корреляции между вариантами обеих выборок при попарном их сопоставлении. Пример. При определении доли влияния системы содержания на конверсию корма на 1 кг прироста живой массы бройлеров различных кроссов было отмечено, что лучший генетический потенциал по данному показателю по всем кроссам выявлен у молодняка, выращенного в реконструированных птичниках с регулируемым микроклиматом (см. табл. 10). Таблица 10 Конверсия корма на 1 кг прироста живой массы высокопродуктивных бройлеров при разных системах содержания
*/ Достоверно выше по сравнению с напольным содержанием в реконструированных птичниках с регулируемым микроклиматом при Р<0,05; **/ при Р<0,01; ***/ при Р<0,001 Определим достоверность различий в показателях по конверсии корма на 1 кг прироста живой массы бройлеров при разных системах содержания. Сравнение проведём с данными при содержании бройлеров в реконструированных птичниках с регулируемым микроклиматом. Вычислим критерий достоверности разности между средними арифметическими для кросса «Смена-4»
Для кросса «Кобб-500»
Для кросса «Арбор-Айкрес"
Дисперсионный анализ Дисперсионный анализ – это статистический метод анализа результатов наблюдений, зависящих от различных, одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния. Дисперсионный анализ находит применение в различных областях науки и техники. Известно, что многие признаки и свойства живых организмов находятся под влиянием различных факторов: наследственности, условий среды, внутренних факторов организма, искусственного отбора. Степень и направленность воздействия различных факторов неодинаковы, поэтому важно определить долю влияния отдельных факторов на изменчивость признака. Для решения подобной задачи используют метод дисперсионного анализа, разработанный Р.Фишером.
Сущность дисперсионного анализа состоит в установлении роли отдельных факторов в изменчивости признака. В зависимости от количества изучаемых факторов различают однофакторный и многофакторный дисперсионный анализ. Рассмотрим подробнее метод однофакторного дисперсионного анализа.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.189.119 (0.009 с.) |

 ,
, - квадрат ошибки средней арифметической 1-го вариационного ряда,
- квадрат ошибки средней арифметической 1-го вариационного ряда, 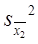 - квадрат ошибки средней арифметической 2-го вариационного ряда,
- квадрат ошибки средней арифметической 2-го вариационного ряда, - искомая ошибка разности.
- искомая ошибка разности.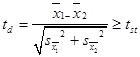
 ,
,
 %
%

 0,01***
0,01***
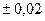 ***
***
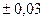
 **
**

 различие достоверно при уровне значимости P<0,001
различие достоверно при уровне значимости P<0,001
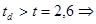 различие достоверно при уровне значимости P<0,01
различие достоверно при уровне значимости P<0,01
 различие недостоверно
различие недостоверно


