
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальный ряд распределения яйценоскостиСодержание книги
Поиск на нашем сайте
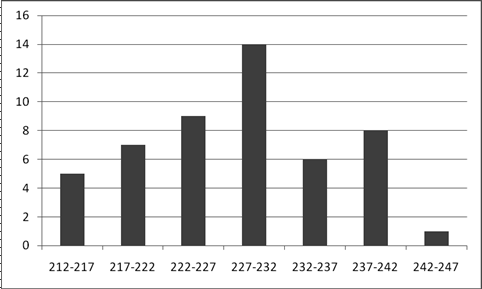
Построим гистограмму распределения яйценоскости (рис. 9).
Р и с. 9. Гистограмма распределения яйценоскости
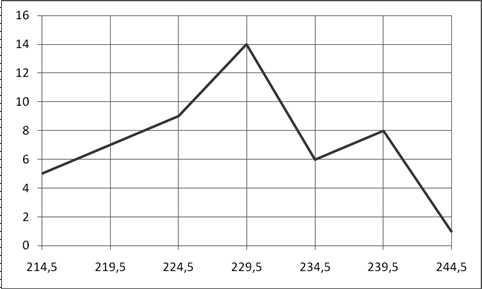
Данные гистограммы показывают характерную для многих признаков форму распределения: чаще встречаются значения средних интервалов признака, реже – крайние (малые и большие) значения признака. Форма этого распределения близка к нормальному закону распределения, которое образуется, если на варьирующую переменную влияет большое число факторов, ни один из которых не имеет преобладающего значения. Полигон и кумулята распределения яйценоскости имеют вид (рис. 10 и 11).
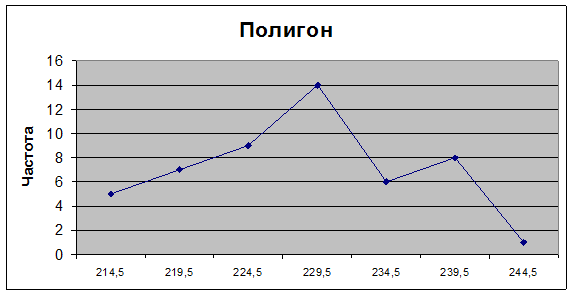
Р и с. 10. Полигон распределения яйценоскости
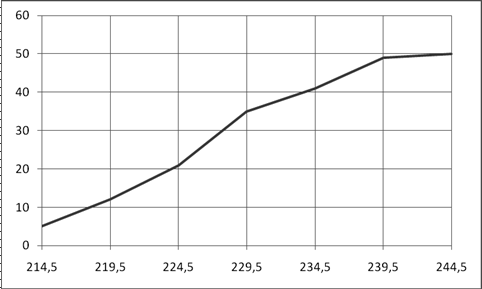
Р и с. 11. Кумулята распределения яйценоскости
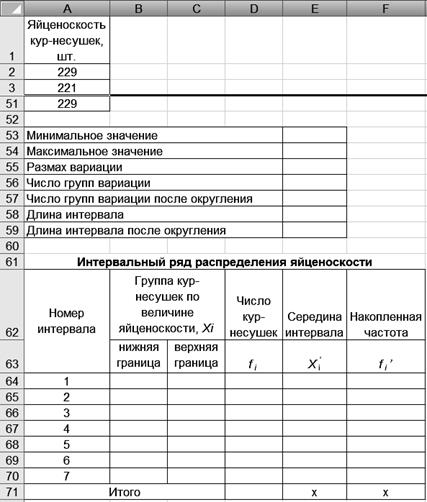
Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 12.
Р и с. 12
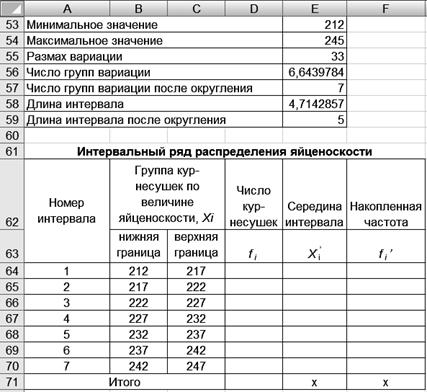
2. Ранжируйте ряд. 2.1. Выделите ячейки А2:А51. 2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Сортировка по возрастанию > 3. Определите величину интервала для построения интервального ряд распределения. 3.1. Скопируйте ячейку А2 в ячейку Е53. 3.2. Скопируйте ячейку А51 в ячейку Е54. 3.3. Рассчитайте размах вариации. Для этого введите в ячейку Е55 формулу =E54-E53. 3.4. Рассчитайте число групп вариации. Для этого введите в ячейку Е56 формулу =1+3,322*LOG10(50). 3.5. Введите в ячейку Е57 округленное число групп. 3.6. Рассчитайте длину интервала. Для этого введите в ячейку Е58 формулу =E55/E57. 3.7. Введите в ячейку Е59 округленную длину интервала. 4. Постройте интервальный ряд. 4.1. Скопируйте ячейку Е53 в ячейку В64. 4.2. Введите в ячейку В65 формулу =B64+$E$59. 4.3. Скопируйте ячейку В65 в ячейки В66:В70. 4.4. Введите в ячейку С64 формулу =B65. 4.5. Введите в ячейку С65 формулу =C64+$E$59. 4.6. Скопируйте ячейку С65 в ячейки С66:С70. Результаты решения выводятся на экран дисплея в следующем виде (рис. 13).
Р и с. 13
5. Рассчитайте частоту интервалов.
5.1. Выполните команду Сервис, Анализ данных, щелкнув поочередно левой кнопкой мыши. 5.2. В диалоговом окне Анализ данных с помощью левой кнопки мыши установите: Инструменты анализа ®<Гистограмма> (рис. 14).
Р и с. 14 5.3. Щелкните левой кнопкой мыши на кнопке <ОК>. 5.4. На вкладке Гистограмма установите параметры в соответствии с рис. 15.
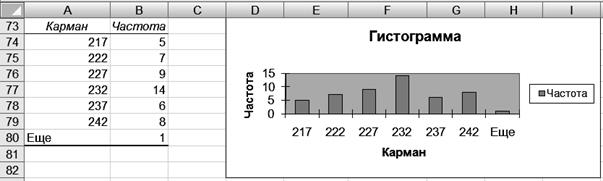
Р и с. 15 5.5. Щелкните левой кнопкой мыши на кнопке <ОК>. Результаты решения выводятся на экран дисплея в следующем виде (рис. 16).
Р и с. 16
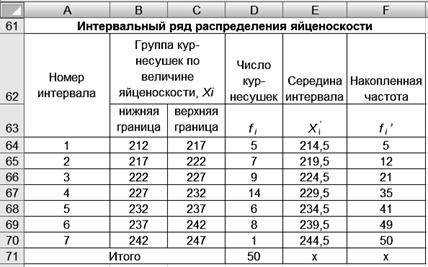
6. Заполните таблицу «Интервальный ряд распределения». 6.1. Скопируйте ячейки В74:В80 в ячейки D64:D70. 6.2. Рассчитайте сумму частот. Для этого выделите ячейки D64:D70 и щелкните левой кнопкой мыши на панели инструментов на кнопке <Автосумма > 6.3. Рассчитайте середину интервалов. Для этого введете в ячейку Е64 формулу =(B64+C64)/2 и скопируйте в ячейки Е65:Е70. 6.4. Рассчитайте накопленные частоты. Для этого скопируйте ячейку D64 в ячейку F64. В ячейку F65 введите формулу =F64+D65 и скопируйте в ячейки F66:F70. Результаты решения выводятся на экран дисплея в следующем виде (рис. 17).
Р и с. 17 7. Отредактируйте гистограмму. 7.1. Щелкните правой кнопкой мыши на диаграмме на названии «карман» и на появившейся вкладке нажмите кнопку <Очистить>. 7.2. Щелкните правой кнопкой мыши на диаграмме и на появившейся вкладке нажмите кнопку <Исходные данные>. 7.3. В диалоговом окне Исходные данные измените подписи оси Х. Для этого выделите ячейки В64:С70 (рис. 18).
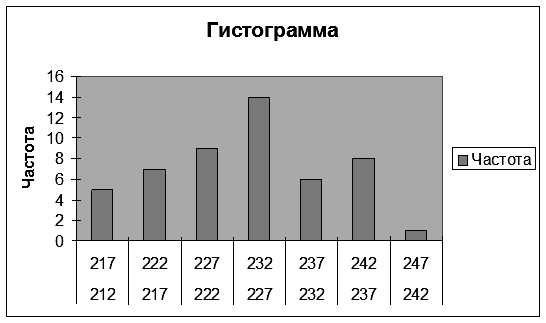
Р и с. 18 7.5. Нажмите клавишу <Enter>. Результаты выводятся на экран дисплея в следующем виде (рис. 19).
Р и с. 19
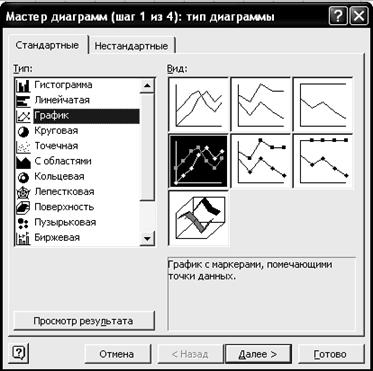
8. Постройте полигон распределения яйценоскости. 8.1. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Мастер диаграмм > 8.2. В диалоговом окне Мастер диаграмм (шаг 1 из 4) с помощью левой кнопки мыши установите: Стандартные ® <График> (рис. 20).
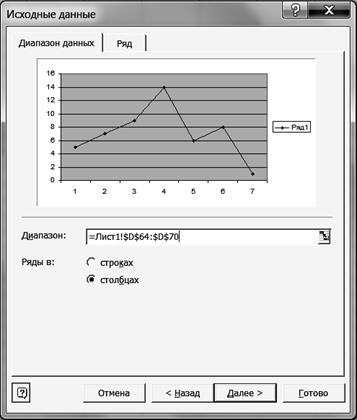
Р и с. 20 8.3. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.4. В диалоговом окне Мастер диаграмм (шаг 2 из 4) установите параметры в соответствии с рис. 21.
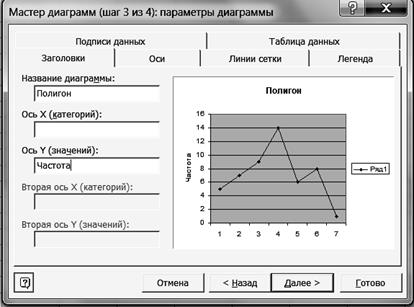
Р и с. 21 8.5. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.6. В диалоговом окне Мастер диаграмм (шаг 3 из 4) введите названия диаграммы и ос Y (рис. 22).
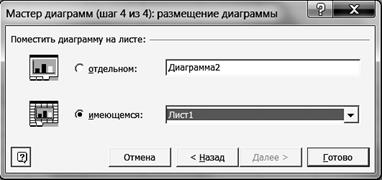
Р и с. 22 8.7. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.8. В диалоговом окне Мастер диаграмм (шаг 4 из 4) установите параметры в соответствии с рис. 23.
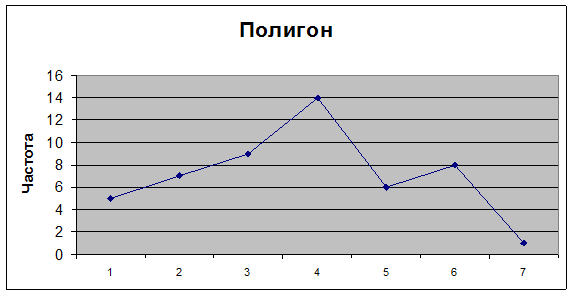
Р и с. 23 8.9. Щелкните левой кнопкой мыши на кнопке <Готово>. Результаты выводятся на экран дисплея в следующем виде (рис. 24).
Р и с. 24
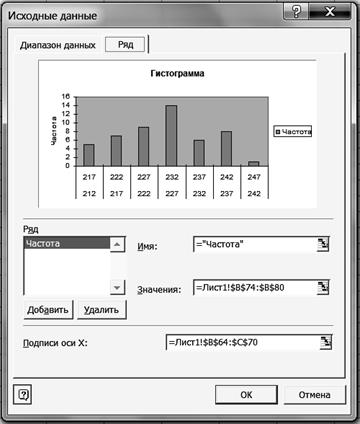
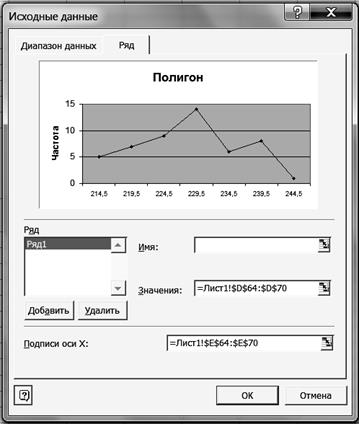
9. Вставьте на графике подписи данных. 9.1. Щелкните правой кнопкой мыши на диаграмме и на появившейся вкладке нажмите кнопку <Исходные данные>. 9.2. В диалоговом окне Исходные данные измените подписи оси Х. Для этого выделите ячейки Е64:Е70 (рис. 25).
Р и с. 25
9.3. Нажмите клавишу <Enter>. Результаты выводятся на экран дисплея в следующем виде (рис. 26).
Р и с. 26
Кумулята распределения строится аналогично полигону распределения на основе накопленных частот.
Средние величины Для того, чтобы количественно охарактеризовать самые существенные свойства распределения, а также для того, чтобы можно было сравнить разные распределения, вычисляют средние показатели - выборочные числовые характеристики. В статистике используются различные величины в зависимости от того, какие цели при анализе материала ставит исследователь. Понятием средней величины пользуемся в тех случаях, когда требуется определить средний надой по стаду, средний привес, средний прирост стада, средние клинические показатели деятельности сердца, лёгких, среднего состава крови и во многих других случаях. Различают следующие виды средних величин: средняя арифметическая ( Наиболее распространенным видом средних величин является средняя арифметическая, которая бывает простой и взвешенной. Средняя арифметическая Средняя арифметическая является наиболее распространенной среди средних величин. Ее применяют в тех случаях, когда даны отдельные объекты с индивидуальными значениями признаков, выраженными абсолютными показателями. Среднюю арифметическую определяют как отношение суммы индивидуальных значений признаков к их количеству. Различают среднюю арифметическую простую и взвешенную. Среднюю арифметическую простую применяют в случае, если индивидуальные значения признака в совокупности встречаются по одному разу, а взвешенную - если индивидуальные значения признака представлены несколькими объектами. Среднюю арифметическую простую определяют по формуле:
где х -варианты; n -число вариант. Формула средней арифметической взвешенной имеет вид:
где f -частота вариант. Рассмотрим методику расчета средней арифметической. Пример. Имеются данные по 8 коровам об их удое за год (табл. 3). Т а б л и ц а 3 Удой коровы
Требуется определить средний удой на одну корову за год. Так как даны индивидуальные значения удоя молока по каждой корове, то средний удой определяется по формуле средней арифметической простой:
Таким образом, среднегодовой удой от коровы за год составляет 3883 кг. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис.27
Р и с. 27 2. Рассчитайте средний удой на корову за год как среднюю арифметическую простую. 2.1. Выделите ячейку С11.
2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СРЗНАЧ> (рис. 28).
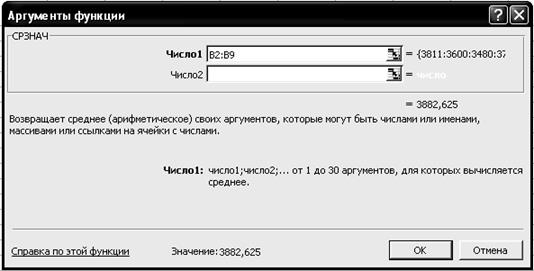
Р и с. 28 2.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.5. На вкладке СРЗНАЧ установите параметры в соответствии с рис. 29.
Р и с. 29 2.6. Щелкните левой кнопкой мыши на кнопке <ОК>. Результаты решения выводятся на экран дисплея в следующем виде (рис. 30).
Р и с. 30
Мода и медиана Средние величины, описанные выше, являются обобщающими характеристиками совокупности по тому или иному признаку. Вспомогательными характеристиками являются, так называемые, структурные средние, к которым относятся мода, квартили, децили, медиана и др. Наиболее употребляемыми являются мода и медиана. Мода - это величина, которая встречается в совокупности наиболее часто, то есть признак с наибольшей частотой. Этот показатель используется в тех случаях, когда требуется охарактеризовать наиболее часто встречающуюся величину признака (наиболее распространенный размер животноводческих ферм на сельскохозяйственных предприятиях, преобладающие цены на сельскохозяйственную продукцию и т. п.). Медианой называется величина, делящая численность упорядоченного вариационного ряда (расположенного в порядке возрастания или убывания признака) на две равные части. Медиана характеризует количественную границу значений изменяющегося признака, которыми обладает половина единиц совокупности. Например, если медианное значение удоя коровы составляет 4735 кг, то это означает, что половина коров имеет удой молока ниже 4735 кг и половина коров выше. В дискретном вариационном ряду модой является признак с наибольшей частотой. Медианой является признак с номером, который находят путем деления суммы частот упорядоченного вариационного ряда на два и добавления 0,5. В интервальном вариационном ряду моду находят по формуле:
где Мо - мода; хМо -нижняя граница модального интервала; hМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным. Модальным интервалом является интервал с наибольшей частотой. Формула расчета медианы в интервальном вариационном ряду:
где Ме - медиана; хМе - нижняя граница медианного интервала;
hМе - величина медианного интервала;
sМе−1 - сумма частот, накопленных в интервалах, предшествующих медианному; fМе - частота медианного интервала. Медианным интервалом является интервал, накопленная частота которого равна или превышает половину суммы частот. Рассмотрим методику расчета моды и медианы. Пример. Имеются данные о продуктивности норок (табл. 4). Т а б л и ца 4 Приплод норок
Требуется определить моду и медиану. Самую большую частоту - 164 имеют норки с приплодом в 4 головы, следовательно, мода равна 4. Медианой будет признак с номером Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 31.
Р и с. 31
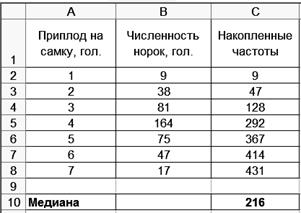
2. Рассчитайте накопленные частоты. 2.1. Скопируйте ячейку В2 в ячейку С2. 2.2.Введите в ячейку С3 формулу =С2+В3. 2.3. Скопируйте ячейку С3 в ячейки С4:С8. 3. Рассчитайте номер медианы. Для этого введите в ячейку С10 формулу =С8/2+0,5. Результаты решения выводятся на экран дисплея в следующем виде (рис. 32).
Р и с. 32
Пример. Имеются данные о среднесуточных приростах живой массы у молодняка крупного рогатого скота (табл. 5). Т а б л и ц а 5 Среднесуточный прирост живой массы ремонтных телок на откорме
Требуется определить моду и медиану. Моду и медиану рассчитывают по формулам для интервального вариационного ряда. Для нахождения моды необходимо определить модальный интервал. Таким будет интервал 575-600 с наибольшей частотой 143. Отсюда мода равна:
Для нахождения медианы надо определить медианный интервал. Половина суммы частот равна 315 (630:2). Следовательно, согласно накопленным частотам медианным интервалом будет 600 - 625 (315 < 434). Медиана равна: Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 33.
Р и с. 33 2. Рассчитайте накопленные частоты. 2.1. Скопируйте ячейку В2 в ячейку С2. 2.2.Введите в ячейку С3 формулу =С2+В3. 2.3. Скопируйте ячейку С3 в ячейки С4:С9. 3. Рассчитайте моду. Для этого введите в ячейку В11 формулу =575+25*(В5−В4)/(2*В5−В4−В6). 4. Рассчитайте моду. Для этого введите в ячейку В12 формулу =600+25*(С9/2−С5)/В5. Результаты решения выводятся на экран дисплея в следующем виде (рис. 34).
Р и с. 34 4. Показатели вариации Для измерения вариации применяют различные показатели, из которых основными являются размах вариации (лимит), среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Размах вариации определяется как разница между наибольшим и наименьшим значениями признака:
где R -размах вариации; x min, xmax- минимальное и максимальное значение признака.
Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных отклонений отдельных вариант от средней арифметической: простое взвешенное где L - среднее линейное отклонение;
х -варианты; n - число вариант; f - частоты. Дисперсию рассчитывают как среднюю арифметическую квадратов отклонений вариант от средней арифметической: простая взвешенная где Среднее квадратическое отклонение равно корню квадратному из дисперсии: простое взвешенное где Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней арифметической величине:
где Рассмотрим методику расчета показателей вариации. Пример. Имеются данные о поголовье бычков, поступивших на мясокомбинат (табл. 6). Т а б л и ц а 6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.123.194 (0.013 с.) |

 .
.
 .
.
 .
.
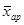 ), средняя геометрическая (
), средняя геометрическая (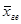 ), средняя квадратическая (
), средняя квадратическая (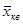 ), средняя гармоническая (
), средняя гармоническая ( ), мода (М0) и медиана Ме.
), мода (М0) и медиана Ме.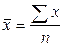 ,
,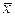 -средняя;
-средняя; ,
,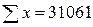
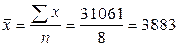 кг.
кг.
 или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.

 ,
,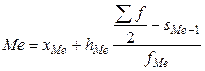 ,
,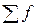 - сумма частот;
- сумма частот;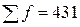
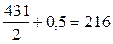 . Из накопленных частот видно, что медианой будет норка, имеющая приплод в 4 головы.
. Из накопленных частот видно, что медианой будет норка, имеющая приплод в 4 головы.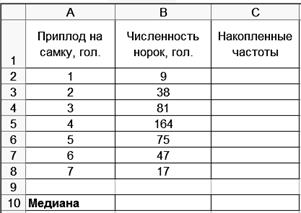
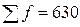
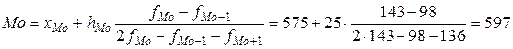 г.
г.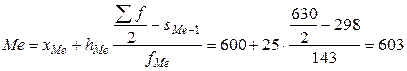 г.
г.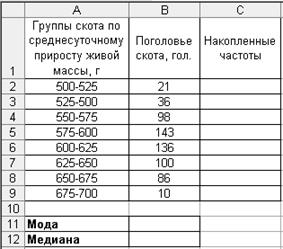

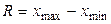 ,
,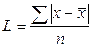 ;
;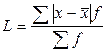 ,
,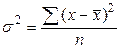 ;
; ,
, - дисперсия.
- дисперсия. ;
;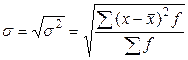 ,
, - среднее квадратическое отклонение
- среднее квадратическое отклонение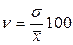 ,
, -коэффициент вариации.
-коэффициент вариации.


