
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднегодовой удой коровы и расход кормов на коровуСодержание книги
Поиск на нашем сайте
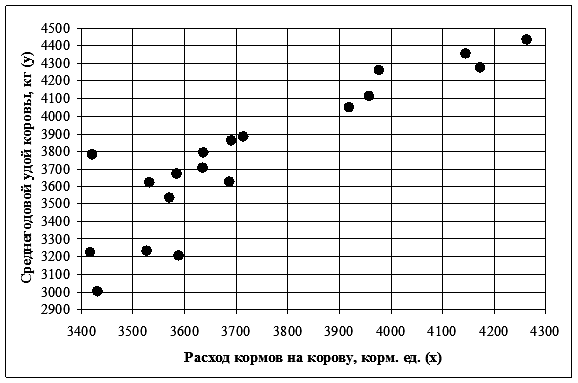
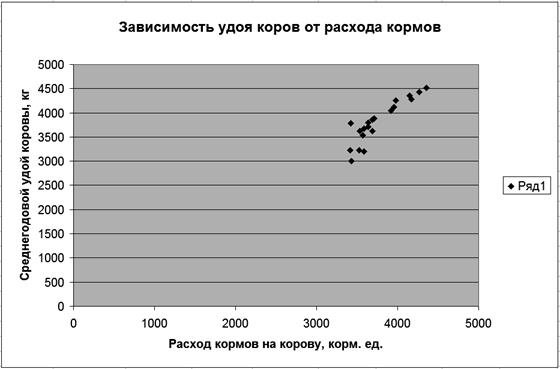
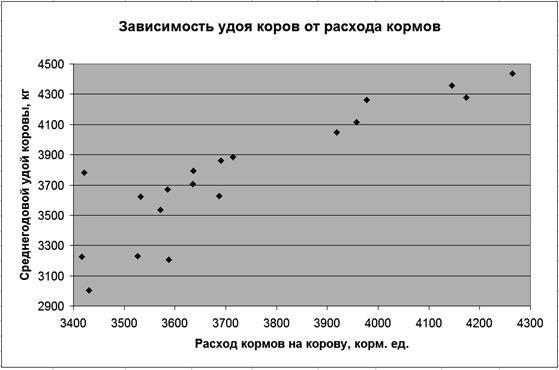
Требуется определить зависимость удоя молока от уровня кормления коров. Анализ данных показывает, что с увеличением расхода кормов среднегодовой удой молока от коровы повышается. Это подтверждает и график (рис. 62).
Р и с. 62. Зависимость удоя коров от расхода кормов
Расположение точек на графике показывает, что связь между признаками имеет прямолинейный характер и поэтому может быть выражена уравнением прямой линии:
Для определения неизвестных параметров уравнения а 0 и а 1 необходимо решить систему нормальных уравнений:
Значения
После решения системы уравнений получим значения параметров:
Уравнение регрессии имеет вид:
Величина а 0 = −1274 в уравнении регрессии не имеет смысла. Коэффициент регрессии а 1 = 1,35 характеризует изменение продуктивности коров по данной совокупности в зависимости от уровня кормления. При увеличении или уменьшении расхода кормов на 1 корм. ед. среднегодовой удой коровы, соответственно увеличивается или уменьшается в среднем на 1,35 кг. Полученное уравнение регрессии, кроме оценки влияния уровня кормления на продуктивность коров, позволяет прогнозировать ее в зависимости от величины данного фактора. При этом, уровень кормления должен находиться в пределах его изменения в исходной выборочной совокупности. Ожидаемый удой молока в зависимости от расхода кормов представлен в последней графе табл. 14. Для оценки тесноты связи рассчитаем коэффициент корреляции:
Его значение близко к единице, поэтому можно утверждать, что полученное уравнение регрессии достаточно хорошо описывает исследуемую зависимость. Коэффициент детерминации r 2 = 0,813 показывает, что 81,3 % колеблемости в среднегодовом удое коровы объясняется уровнем кормления. Оценим достоверность коэффициента корреляции с помощью F -критерия и t -критерия Стьюдента. Фактическое значение F -критерия равно:
Табличное значение F -критерия при уровне значимости 0,05 и при Фактическое значение критерия выше табличного, поэтому с вероятностью 0,95 можно утверждать, что связь между признаками достоверна, и уравнение регрессии в полной мере отражает эту связь. Фактическое значение t -критерия равно:
Табличное значение t -критерия при уровне значимости 0,05 и при Фактическое значение критерия выше табличного, следовательно, вывод о достоверности связи между признаками подтверждается. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 63.
Р и с. 63
2. Для установления формы связи постройте график зависимости среднегодового удоя коров от расхода кормов. 2.1. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Мастер диаграмм > 2.2. В диалоговом окне Мастер диаграмм (шаг 1 из 4) с помощью левой кнопки мыши установите: Стандартные ® <График> (рис. 64).
Р и с. 64
2.3. Щелкните левой кнопкой мыши на кнопке <Далее>. 2.4. В диалоговом окне Мастер диаграмм (шаг 2 из 4) щелкните левой кнопкой мыши на кнопке <Добавить> (рис. 65).
Р и с. 65
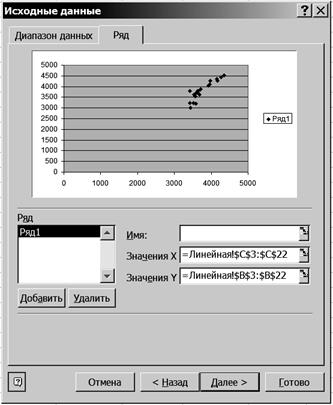
2.5. На вкладке Источник данных установите параметры в соответствии с рис. 66.
Р и с. 66
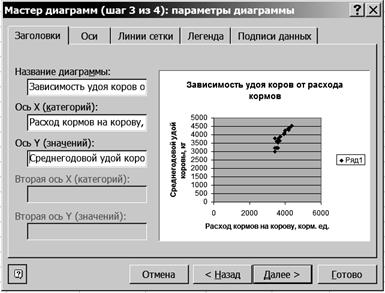
2.6. Щелкните левой кнопкой мыши на кнопке <Далее>. 2.7. В диалоговом окне Мастер диаграмм (шаг 3 из 4) введите названия диаграммы и ос Y (рис. 67).
Р и с. 67
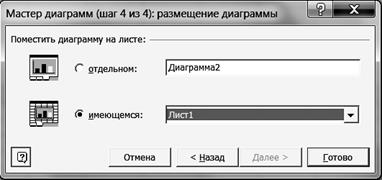
2.8. Щелкните левой кнопкой мыши на кнопке <Далее>. 2.9. В диалоговом окне Мастер диаграмм (шаг 4 из 4) установите параметры в соответствии с рис. 68.
Р и с. 68
2.10. Щелкните левой кнопкой мыши на кнопке <Готово>. Результаты решения выводятся на экран дисплея в следующем виде (рис. 69).
Р и с. 69
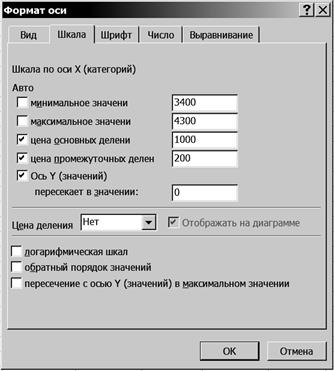
3. Измените формат осей. 3.1. Установите курсор на ось Х (категорий), щелкните правой кнопкой мыши, в появившемся контекстном меню выберите команду Формат оси и щелкните левой или правой кнопкой мыши (рис. 70). 3.2. Измените формат оси Х. На вкладке Формат оси установите параметры в соответствии с рис. 70.
Р и с. 70
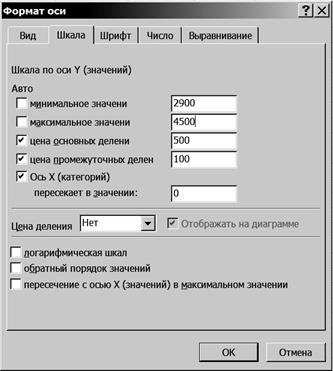
3.3. Щелкните левой кнопкой мыши на кнопке <ОК>. 3.4. Установите курсор на ось Y (категорий), щелкните правой кнопкой мыши, в появившемся контекстном меню выберите команду Формат оси и щелкните левой или правой кнопкой мыши (рис. 71). 3.5. Измените формат оси Y. На вкладке Формат оси установите параметры в соответствии с рис. 71.
Р и с. 71
3.6. Щелкните левой кнопкой мыши на кнопке <ОК>. Результаты решения выводятся на экран дисплея в следующем виде (рис. 72).
Р и с. 72
График показывает, что связь между признаками имеет прямолинейный характер и поэтому может быть выражена уравнением прямой линии:
Для определения параметров уравнения втабличном процессоре Microsoft Excel можно использовать статистическую функцию ЛИНЕЙН или надстройку Анализ данных.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.83.96 (0.006 с.) |

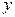
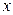
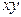
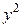
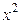
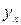
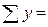 = 76158
= 76158
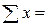 = 75222
= 75222
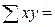 = 288629892
= 288629892
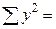 = 293644980
= 293644980
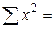 = 284539942
= 284539942
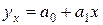 .
.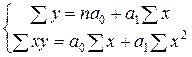
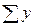 ,
, 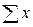 ,
,  и
и 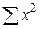 определим по данным наблюдений (табл. 14) и подставим в уравнения:
определим по данным наблюдений (табл. 14) и подставим в уравнения: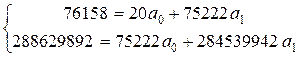
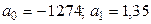 .
.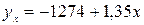 .
.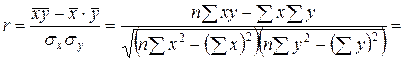
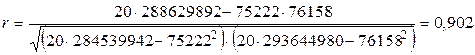 .
.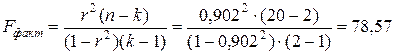 .
.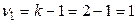 и
и 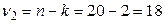 степенях свободы вариации составляет 4,41 (таблица «Значение F -критерия Фишера при уровне значимости 0,05»).
степенях свободы вариации составляет 4,41 (таблица «Значение F -критерия Фишера при уровне значимости 0,05»).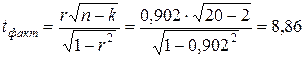 .
.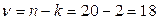 степенях свободы вариации составляет 2,1009 (таблица «Значение t -критерия Стьюдента при уровне значимости 0,10, 0,05 и 0,01»).
степенях свободы вариации составляет 2,1009 (таблица «Значение t -критерия Стьюдента при уровне значимости 0,10, 0,05 и 0,01»).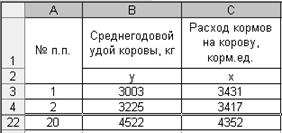
 .
.
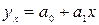 .
.


