
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Элементы теории вероятностейСодержание книги
Поиск на нашем сайте
Предисловие Курс теории вероятностей и математической статистики входит в цикл фундаментальных дисциплин, изучение которых является обязательным для студентов сельскохозяйственных учебных заведений. Одной из важнейших сфер приложения теории вероятностей и математической статистики является животноводство. Развитие современного животноводства сопровождается накоплением большого количества информации по многим вопросам генетики, селекции, продуктивности, здоровья животных, поведенческих функций и т.д. В задачу науки входят классификация, упорядочение и систематизация этих данных, их научный анализ. Подобный подход позволяет формулировать практические предложения, способствующие ускорению развития тех или иных отраслей животноводства, совершенствовать и создавать новые перспективные отрасли, прогнозировать развитие того или иного направления. В ветеринарии, дополнительно к перечисленным возможностям, использование научного анализа позволяет теоретически моделировать течение болезни или действия лечебных факторов и разрабатывать методы профилактики и лечения животных. Все это обуславливает широкое внедрение в зооинженерную и ветеринарную практику математических методов, в том числе математической статистики. Основные теоретические положения математической статистики базируются на теории вероятностей. Основное отличие математической статистики от теории вероятностей в том, что в математической статистике рассматриваются не только действия над законами распределения и числовыми характеристиками, но и приближенные методы отыскания этих законов и характеристик по результатам экспериментов. Цель данных учебно-методических указаний – помочь изучающим теорию вероятностей и математическую статистику в усвоении необходимых теоретических знаний и приобретении практических навыков для квалифицированного использования статистической информации в целях принятия правильных решений в вопросах прогнозирования. I. Элементы теории вероятностей Случайные величины. Вероятность случайного события Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Обозначим: X, Y, Z – случайные величины
Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения с определенными вероятностями. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины, независимо от величины промежутка, бесконечно. Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность. Вероятность (Р) показывает степень возможности осуществления данного события, явления, результата.
Вероятность невозможного события равна нулю, достоверного — единице (100%). Вероятность любого события лежит в пределах от 0 до 1 - в зависимости от того, насколько это событие случайно.
II. Элементы математической статистики Яйценоскость кур-несушек
Требуется построить интервальный ряд распределения и отобразить его графически в виде гистограммы, полигона и кумуляты. Видно, что признак варьирует от 212 до 245 яиц, полученных от несушки за 1 год. В нашем примере по формуле Стерждесса определим число групп: k = 1 + 3,322 lg 50 = 6,643 ≈ 7. Рассчитаем длину (размах) интервала по формуле:
Построим интервальный ряд с 7 группами и интервалом 5 шт. яиц (табл. 2). Для построения графиков в таблице рассчитаем середину интервалов и накопленную частоту. Т а б л и ц а 2 Средние величины Для того, чтобы количественно охарактеризовать самые существенные свойства распределения, а также для того, чтобы можно было сравнить разные распределения, вычисляют средние показатели - выборочные числовые характеристики. В статистике используются различные величины в зависимости от того, какие цели при анализе материала ставит исследователь. Понятием средней величины пользуемся в тех случаях, когда требуется определить средний надой по стаду, средний привес, средний прирост стада, средние клинические показатели деятельности сердца, лёгких, среднего состава крови и во многих других случаях. Различают следующие виды средних величин: средняя арифметическая ( Наиболее распространенным видом средних величин является средняя арифметическая, которая бывает простой и взвешенной. Средняя арифметическая Средняя арифметическая является наиболее распространенной среди средних величин. Ее применяют в тех случаях, когда даны отдельные объекты с индивидуальными значениями признаков, выраженными абсолютными показателями. Среднюю арифметическую определяют как отношение суммы индивидуальных значений признаков к их количеству. Различают среднюю арифметическую простую и взвешенную. Среднюю арифметическую простую применяют в случае, если индивидуальные значения признака в совокупности встречаются по одному разу, а взвешенную - если индивидуальные значения признака представлены несколькими объектами. Среднюю арифметическую простую определяют по формуле:
где х -варианты; n -число вариант. Формула средней арифметической взвешенной имеет вид:
где f -частота вариант. Рассмотрим методику расчета средней арифметической. Пример. Имеются данные по 8 коровам об их удое за год (табл. 3). Т а б л и ц а 3 Удой коровы
Требуется определить средний удой на одну корову за год. Так как даны индивидуальные значения удоя молока по каждой корове, то средний удой определяется по формуле средней арифметической простой:
Таким образом, среднегодовой удой от коровы за год составляет 3883 кг. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис.27
Р и с. 27 2. Рассчитайте средний удой на корову за год как среднюю арифметическую простую. 2.1. Выделите ячейку С11. 2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СРЗНАЧ> (рис. 28).
Р и с. 28 2.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.5. На вкладке СРЗНАЧ установите параметры в соответствии с рис. 29.
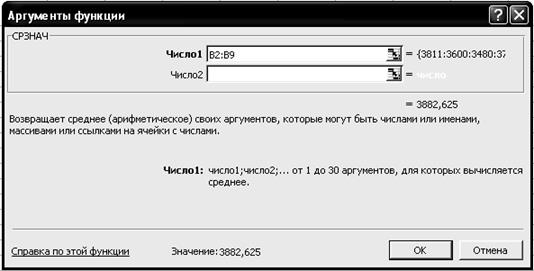
Р и с. 29 2.6. Щелкните левой кнопкой мыши на кнопке <ОК>. Результаты решения выводятся на экран дисплея в следующем виде (рис. 30).
Р и с. 30
Мода и медиана Средние величины, описанные выше, являются обобщающими характеристиками совокупности по тому или иному признаку. Вспомогательными характеристиками являются, так называемые, структурные средние, к которым относятся мода, квартили, децили, медиана и др. Наиболее употребляемыми являются мода и медиана. Мода - это величина, которая встречается в совокупности наиболее часто, то есть признак с наибольшей частотой. Этот показатель используется в тех случаях, когда требуется охарактеризовать наиболее часто встречающуюся величину признака (наиболее распространенный размер животноводческих ферм на сельскохозяйственных предприятиях, преобладающие цены на сельскохозяйственную продукцию и т. п.). Медианой называется величина, делящая численность упорядоченного вариационного ряда (расположенного в порядке возрастания или убывания признака) на две равные части. Медиана характеризует количественную границу значений изменяющегося признака, которыми обладает половина единиц совокупности. Например, если медианное значение удоя коровы составляет 4735 кг, то это означает, что половина коров имеет удой молока ниже 4735 кг и половина коров выше. В дискретном вариационном ряду модой является признак с наибольшей частотой. Медианой является признак с номером, который находят путем деления суммы частот упорядоченного вариационного ряда на два и добавления 0,5. В интервальном вариационном ряду моду находят по формуле:
где Мо - мода; хМо -нижняя граница модального интервала; hМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным. Модальным интервалом является интервал с наибольшей частотой. Формула расчета медианы в интервальном вариационном ряду:
где Ме - медиана; хМе - нижняя граница медианного интервала; hМе - величина медианного интервала;
sМе−1 - сумма частот, накопленных в интервалах, предшествующих медианному; fМе - частота медианного интервала. Медианным интервалом является интервал, накопленная частота которого равна или превышает половину суммы частот. Рассмотрим методику расчета моды и медианы. Пример. Имеются данные о продуктивности норок (табл. 4). Т а б л и ца 4 Приплод норок
Требуется определить моду и медиану. Самую большую частоту - 164 имеют норки с приплодом в 4 головы, следовательно, мода равна 4. Медианой будет признак с номером Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 31.
Р и с. 31
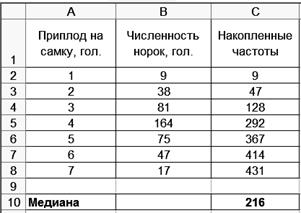
2. Рассчитайте накопленные частоты. 2.1. Скопируйте ячейку В2 в ячейку С2. 2.2.Введите в ячейку С3 формулу =С2+В3. 2.3. Скопируйте ячейку С3 в ячейки С4:С8. 3. Рассчитайте номер медианы. Для этого введите в ячейку С10 формулу =С8/2+0,5. Результаты решения выводятся на экран дисплея в следующем виде (рис. 32).
Р и с. 32
Пример. Имеются данные о среднесуточных приростах живой массы у молодняка крупного рогатого скота (табл. 5). Т а б л и ц а 5 Среднесуточный прирост живой массы ремонтных телок на откорме
Требуется определить моду и медиану. Моду и медиану рассчитывают по формулам для интервального вариационного ряда. Для нахождения моды необходимо определить модальный интервал. Таким будет интервал 575-600 с наибольшей частотой 143. Отсюда мода равна:
Для нахождения медианы надо определить медианный интервал. Половина суммы частот равна 315 (630:2). Следовательно, согласно накопленным частотам медианным интервалом будет 600 - 625 (315 < 434). Медиана равна: Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 33.
Р и с. 33 2. Рассчитайте накопленные частоты. 2.1. Скопируйте ячейку В2 в ячейку С2. 2.2.Введите в ячейку С3 формулу =С2+В3. 2.3. Скопируйте ячейку С3 в ячейки С4:С9. 3. Рассчитайте моду. Для этого введите в ячейку В11 формулу =575+25*(В5−В4)/(2*В5−В4−В6). 4. Рассчитайте моду. Для этого введите в ячейку В12 формулу =600+25*(С9/2−С5)/В5. Результаты решения выводятся на экран дисплея в следующем виде (рис. 34).
Р и с. 34 4. Показатели вариации Для измерения вариации применяют различные показатели, из которых основными являются размах вариации (лимит), среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Размах вариации определяется как разница между наибольшим и наименьшим значениями признака:
где R -размах вариации; x min, xmax- минимальное и максимальное значение признака. Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных отклонений отдельных вариант от средней арифметической: простое взвешенное где L - среднее линейное отклонение;
х -варианты; n - число вариант; f - частоты. Дисперсию рассчитывают как среднюю арифметическую квадратов отклонений вариант от средней арифметической: простая взвешенная где Среднее квадратическое отклонение равно корню квадратному из дисперсии: простое взвешенное где Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней арифметической величине:
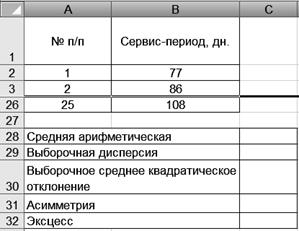
где Рассмотрим методику расчета показателей вариации. Пример. Имеются данные о поголовье бычков, поступивших на мясокомбинат (табл. 6). Т а б л и ц а 6 Сервис-период коров
Требуется рассчитать основные статистические показатели распределения, характеризующие данную выборочную совокупность. Средняя продолжительность сервис-периода коров:
Выборочная дисперсия сервис-периода коров:
Выборочное среднее квадратическое отклонение сервис-периода коров:
Асимметрия сервис-периода коров:
Эксцесс сервис-периода коров:
Полученные значения асимметрии и эксцесса показывают, что данное распределение имеет правостороннюю асимметрию и более высокую вариацию, чем при нормальном распределении. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 39.
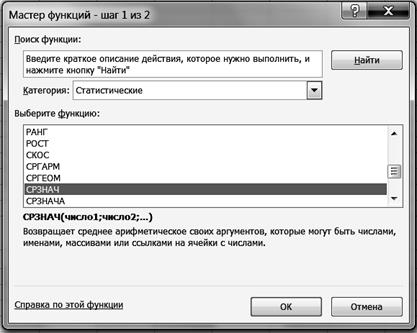
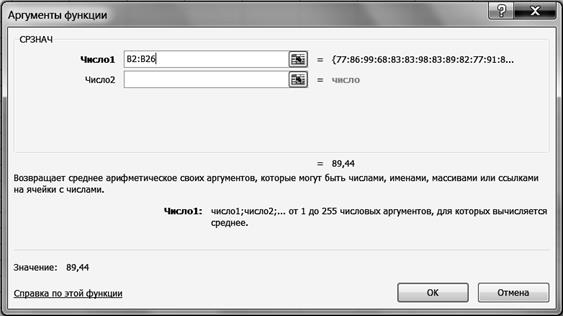
Р и с39 2. Рассчитайте средний сервис-период коров. 2.1. Выделите ячейку С28. 2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СРЗНАЧ> (рис. 40).
Р и с. 40
2.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.5. На вкладке СРЗНАЧ установите параметры в соответствии с рис. 41.
Р и с. 41
2.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 3. Рассчитайте выборочную дисперсию. Для этого используйте статистическую функцию ДИСПА. 4. Рассчитайте выборочное среднее квадратическое отклонение. Для этого используйте статистическую функцию СТАНДОКЛОНА. 5. Рассчитайте асимметрию. Для этого используйте статистическую функцию СКОС. 6. Рассчитайте эксцесс. Для этого используйте статистическую функцию ЭКСЦЕСС. Результаты решения выводятся на экран дисплея в следующем виде (рис. 42).
Р и с. 42
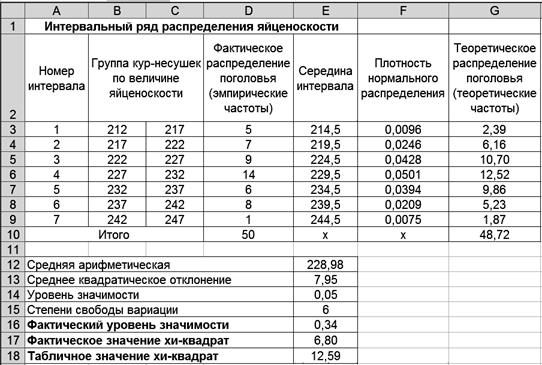
Распределение поголовья
Требуется установить соответствие данного распределения нормальному с уровнем вероятности 0,95. Проверка гипотезы о соответствии теоретическому распределению предполагает расчет теоретических частот этого распределения. Для нормального распределения порядок расчета этих частот следующий: 1) по эмпирическим данным рассчитывают среднюю арифметическую ряда 2) находят нормированное отклонение t каждого эмпирического значения от средней арифметической:
3) по формуле или с помощью таблиц интеграла вероятностей Лапласа находят значение плотности нормального распределения φ (t):
где s – выборочное среднее квадратическое отклонение; π = 3,141593 – постоянное число (отношение длины окружности к ее диаметру); e = 2,718282 – основание натурального логарифма; 4) вычисляют теоретические частоты f0 по формуле:
где n − число вариант (сумма частот); h – величина интервала. Фактическое значение критерия Поскольку фактическое значение критерия меньше табличного, то нулевая гипотеза о соответствии эмпирического распределения теоретическому принимается. Распределение яйценоскости кур-несушек соответствует нормальному распределению. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 43.
Р и с. 43
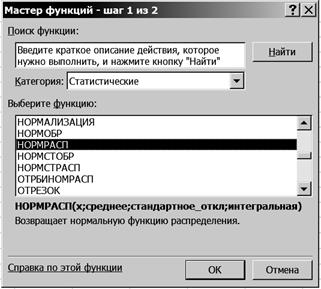
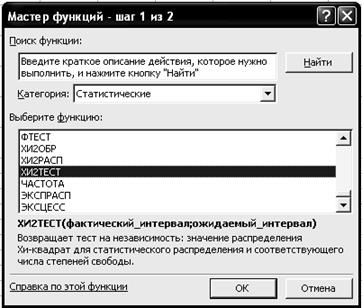
2. Рассчитайте плотность нормального распределения поголовья. 2.1. Выделите ячейку F3. 2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <НОРМРАСП> (рис. 44).
Р и с. 44
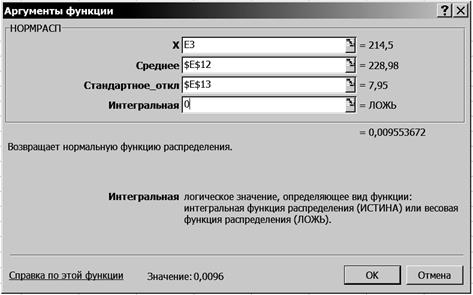
2.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.5. На вкладке НОРМРАСП установите параметры в соответствии с рис. 45.
Р и с. 45
2.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.7. Скопируйте ячейку F3 в ячейки F4:F9. 3. Рассчитайте теоретическое распределение поголовья. 3.1. Введите в ячейку G3 формулу =$D$10*(C3-B3)*F3. 3.2. Скопируйте ячейку G3 в ячейки G4:G9. 3.3. Выделите ячейку G10. 3.4. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > 3.5. Выделите ячейки G3:G9. 3.6. Нажмите клавишу <Enter>. 4. Рассчитайте степени свободы вариации. Введите в ячейку Е15 формулу =(2-1)*(A9-1). 5. Рассчитайте фактический уровень значимости. 5.1. Выделите ячейку Е16. 5.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 5.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ТЕСТ> (рис. 46).
Р и с. 46
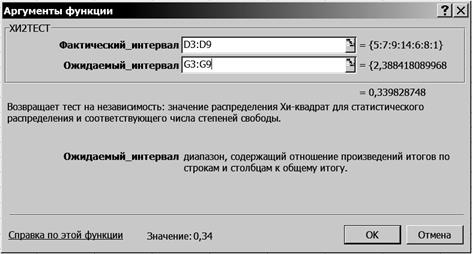
5.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 5.5. На вкладке ХИ2ТЕСТ установите параметры в соответствии с рис. 47.
Р и с. 47
5.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 6. Рассчитайте фактическое значение критерия 6.1. Выделите ячейку Е17. 6.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 6.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ОБР> (рис. 48).
Р и с. 48
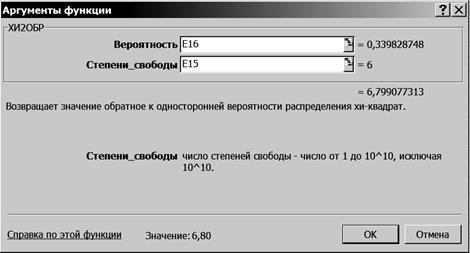
6.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 6.5. На вкладке ХИ2ОБР установите параметры в соответствии с рис. 49.
Р и с. 49 6.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 7. Определите табличное значение критерия Результаты решения выводятся на экран дисплея в следующем виде (рис. 50).
Р и с. 50
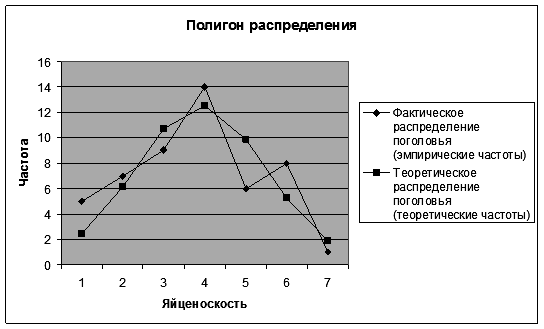
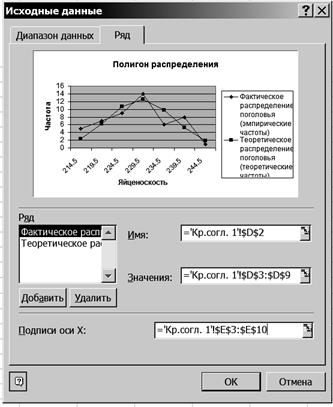
8. Постройте полигон фактического и теоретического распределения поголовья по яйценоскости. 8.1. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Мастер диаграмм > 8.2. В диалоговом окне Мастер диаграмм (шаг 1 из 4) с помощью левой кнопки мыши установите: Стандартные ® <График> (рис. 51).
Р и с. 51 8.3. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.4. В диалоговом окне Мастер диаграмм (шаг 2 из 4) установите параметры в соответствии с рис. 52.
Р и с. 52 8.5. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.6. В диалоговом окне Мастер диаграмм (шаг 3 из 4) введите названия диаграммы и ос Y (рис. 53).
Р и с. 53
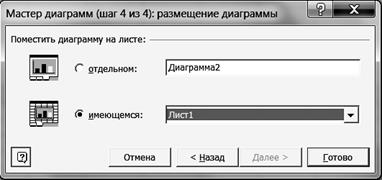
8.7. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.8. В диалоговом окне Мастер диаграмм (шаг 4 из 4) установите параметры в соответствии с рис. 54.
Р и с. 54
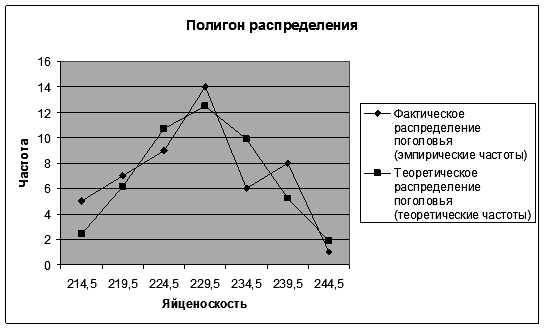
8.9. Щелкните левой кнопкой мыши на кнопке <Готово>. Результаты выводятся на экран дисплея в следующем виде (рис. 55).
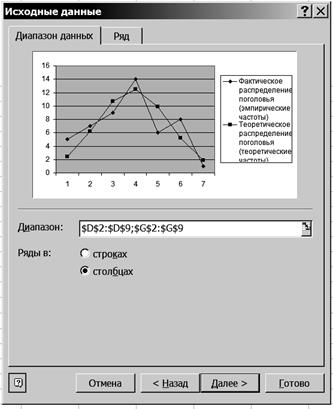
Р и с. 55 9. Вставьте на графике подписи данных. 9.1. Щелкните правой кнопкой мыши на диаграмме и на появившейся вкладке нажмите кнопку <Исходные данные>. 9.2. В диалоговом окне Исходные данные измените подписи оси Х. Для этого выделите ячейки Е64:Е70 (рис. 56).
Р и с. 56 9.3. Нажмите клавишу <Enter>. Результаты выводятся на экран дисплея в следующем виде (рис. 57).
Р и с. 57
Уровень вероятности
Если вычисленное значение t будет меньше 2,0, то выборочный параметр недостоверен, т.е. он не характеризует генеральную совокупность и выводы, полученные при этом, не могут быть распространены на генеральную совокупность. Бывает, что недостоверность вызвана небольшим числом наблюдений, поэтому следует увеличить объём выборки и заново ставить эксперимент. При малом числе наблюдений (n < 30) на величину t влияет объём выборки. Чем меньше выборка, тем менее точно величина t позволяет судить о достоверности выборочной средней. Эту особенность значения изучил английский учённый Госсет (Стъюдент), который разработал таблицы значений t в зависимости от числа наблюдений. Чем меньше число наблюдений, тем больше значение t для одного и того же уровня вероятности. Значения t даны при различном числе степеней свободы. Под числом степеней свободы понимается количество вариантов, которые могут принимать произвольные значения, не меняя величины средней (k= n-1).
Дисперсионный анализ Дисперсионный анализ – это статистический метод анализа результатов наблюдений, зависящих от различных, одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния. Дисперсионный анализ находит применение в различных областях науки и техники. Известно, что многие признаки и свойства живых организмов находятся под влиянием различных факторов: наследственности, условий среды, внутренних факторов организма, искусственного отбора. Степень и направленность воздействия различных факторов неодинаковы, поэтому важно определить долю влияния отдельных факторов на изменчивость признака. Для решения подобной задачи используют метод дисперсионного анализа, разработанный Р.Фишером. Сущность дисперсионного анализа состоит в установлении роли отдельных факторов в изменчивости признака. В зависимости от количества изучаемых факторов различают однофакторный и многофакторный дисперсионный анализ. Рассмотрим подробнее метод однофакторного дисперсионного анализа. Температура тела животных
Физический фактор А (ультрафиолетовое излучение) имеет В данном эксперименте число проведенных наблюдений при действии каждого из уровней фактора одинаково. Все значения величины Х, наблюдаемые при каждом фиксированном уровне фактора Аj, составляют группу, и в последней строке таблицы представлены соответствующие выборочные групповые средние, вычисленные по формуле
Здесь n – число испытаний,
Введем следующие понятия: Факторная сумма квадратов отклонений групповых средних от общей средней
Остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней
Общая сумма квадратов отклонений наблюдаемых значений от общей средней
Можно доказать следующее равенство:
С помощью | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

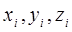 – возможные значения случайных величин.
– возможные значения случайных величин.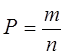 , где n – общее число элементарных исходов (результатов испытания), m – число исходов, благоприятных случайному событию.
, где n – общее число элементарных исходов (результатов испытания), m – число исходов, благоприятных случайному событию. .
.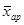 ), средняя геометрическая (
), средняя геометрическая (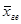 ), средняя квадратическая (
), средняя квадратическая (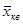 ), средняя гармоническая (
), средняя гармоническая ( ), мода (М0) и медиана Ме.
), мода (М0) и медиана Ме.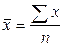 ,
,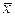 -средняя;
-средняя; ,
,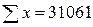
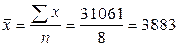 кг.
кг.
 или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.

 ,
,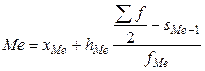 ,
,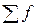 - сумма частот;
- сумма частот;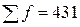
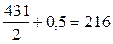 . Из накопленных частот видно, что медианой будет норка, имеющая приплод в 4 головы.
. Из накопленных частот видно, что медианой будет норка, имеющая приплод в 4 головы.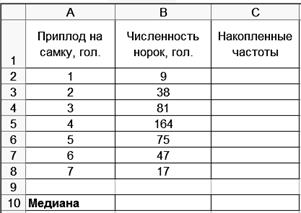
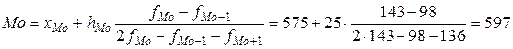 г.
г.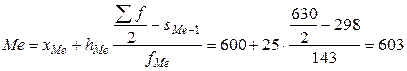 г.
г.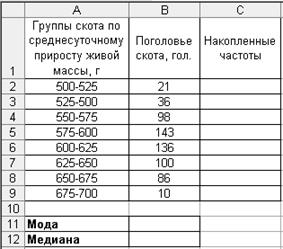

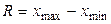 ,
,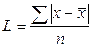 ;
;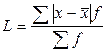 ,
,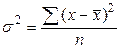 ;
; ,
, - дисперсия.
- дисперсия. ;
;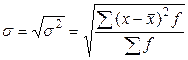 ,
, - среднее квадратическое отклонение
- среднее квадратическое отклонение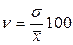 ,
, -коэффициент вариации.
-коэффициент вариации.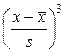
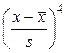

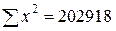
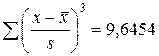

 дн.
дн.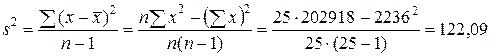 .
. дн.
дн.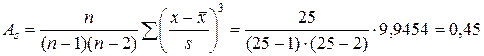 .
.
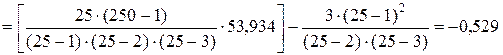 .
.

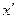
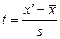
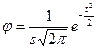

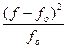
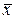 и среднее квадратическое отклонение s;
и среднее квадратическое отклонение s;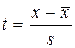 ;
;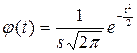 ,
, ,
,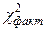 равно 6,8. Табличное значение критерия
равно 6,8. Табличное значение критерия  при заданном уровне значимости
при заданном уровне значимости 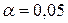 и
и 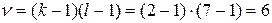 степенях свободы вариации равно 12,592 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).
степенях свободы вариации равно 12,592 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).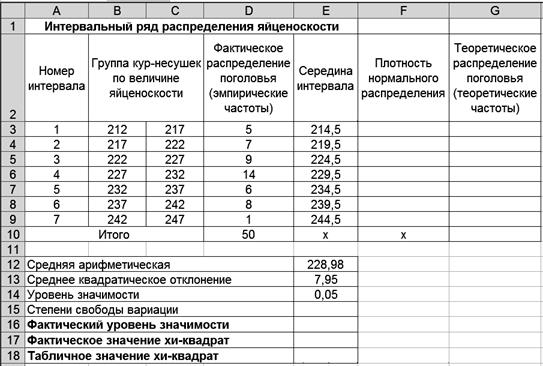
 .
.

 .
.

 )
)
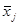
 постоянных уровней (3 различных мощности облучения). На всех уровнях распределения случайной величины Х (температуры тела животного) предполагается нормальным, а дисперсии одинаковыми, хотя и неизвестными.
постоянных уровней (3 различных мощности облучения). На всех уровнях распределения случайной величины Х (температуры тела животного) предполагается нормальным, а дисперсии одинаковыми, хотя и неизвестными. .
. – номер столбца,
– номер столбца, 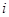 - номер строки, в которой расположено данное значение случайной величины. Общая средняя арифметическая всех
- номер строки, в которой расположено данное значение случайной величины. Общая средняя арифметическая всех 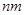 наблюдений находится как
наблюдений находится как .
.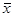 , которая характеризует рассеивание «между группами» (т.е. рассеивание за счет исследуемого фактора):
, которая характеризует рассеивание «между группами» (т.е. рассеивание за счет исследуемого фактора):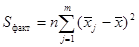 ,
,
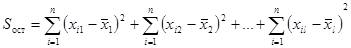 .
.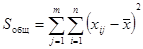 ,
,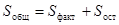 .
. ,
, 


