Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближённое распределение которой известно. Обозначим эту величину в целях общности через Статистическим критерием (или просто критерием) называют случайную величину Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия Эта величина случайная, потому что в различных опытах дисперсии принимают различные, наперёд неизвестные значения, и распределена по закону Фишера-Снедекора. Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия. Наблюдаемым значением После выбора определённого критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают. Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают. Поскольку критерий Критическими точками (границами) Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области. Правосторонней называют критическую область, определяемую неравенством Левосторонней называют критическую область, определяемую неравенством Односторонней называют правостороннюю или левостороннюю критическую область. Двусторонней называют критическую область, определяемую неравенствами В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами (в предположении, что
7.4. Критерий c 2 как критерий согласия Критерий c 2 как критерий согласия используют при проверке принадлежности эмпирического распределения к теоретическому, например, к нормальному, биноминальному, распределению Пуассона и т. п. В этом случае значение критерия c 2 определяют, исходя из частот (f) эмпирического распределения и частот (fo) теоретического распределения:
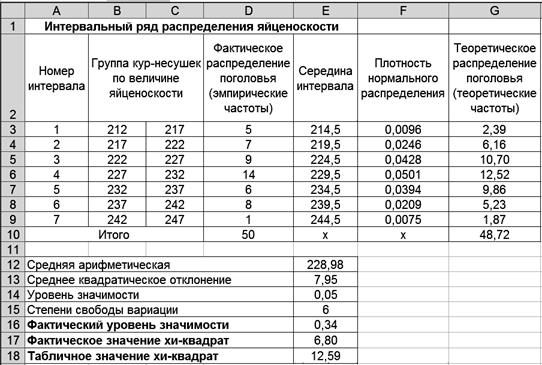
При этом возможны случаи, когда теоретические частоты заранее известны и когда неизвестны. Во втором случае теоретические частоты определяют на основе теоретического распределения исходя из численности выборки. При проверке гипотезы о соответствии эмпирического распределения теоретическому сравнивают фактическое значение критерия Рассмотрим методику применения критерия c 2 как критерия согласия. Пример. В результате учета яйценоскости 50 кур-несушек, содержащихся на птицеферме, был построен интервальный вариационный ряд (табл. 8). Средняя арифметическая ряда равна 228,8, а выборочное среднее квадратическое отклонение – 7,95. Т а б л и ц а 8 Распределение поголовья
Требуется установить соответствие данного распределения нормальному с уровнем вероятности 0,95. Проверка гипотезы о соответствии теоретическому распределению предполагает расчет теоретических частот этого распределения. Для нормального распределения порядок расчета этих частот следующий: 1) по эмпирическим данным рассчитывают среднюю арифметическую ряда 2) находят нормированное отклонение t каждого эмпирического значения от средней арифметической:
3) по формуле или с помощью таблиц интеграла вероятностей Лапласа находят значение плотности нормального распределения φ (t):
где s – выборочное среднее квадратическое отклонение; π = 3,141593 – постоянное число (отношение длины окружности к ее диаметру); e = 2,718282 – основание натурального логарифма; 4) вычисляют теоретические частоты f0 по формуле:
где n − число вариант (сумма частот); h – величина интервала. Фактическое значение критерия Поскольку фактическое значение критерия меньше табличного, то нулевая гипотеза о соответствии эмпирического распределения теоретическому принимается. Распределение яйценоскости кур-несушек соответствует нормальному распределению. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 43.
Р и с. 43
2. Рассчитайте плотность нормального распределения поголовья. 2.1. Выделите ячейку F3. 2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <НОРМРАСП> (рис. 44).
Р и с. 44
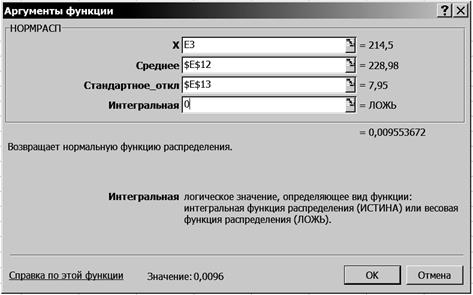
2.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.5. На вкладке НОРМРАСП установите параметры в соответствии с рис. 45.
Р и с. 45
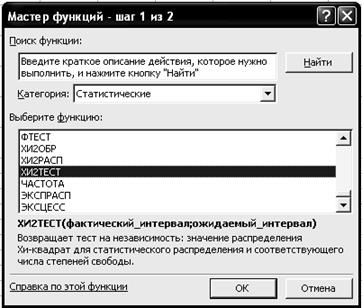
2.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.7. Скопируйте ячейку F3 в ячейки F4:F9. 3. Рассчитайте теоретическое распределение поголовья. 3.1. Введите в ячейку G3 формулу =$D$10*(C3-B3)*F3. 3.2. Скопируйте ячейку G3 в ячейки G4:G9. 3.3. Выделите ячейку G10. 3.4. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > 3.5. Выделите ячейки G3:G9. 3.6. Нажмите клавишу <Enter>. 4. Рассчитайте степени свободы вариации. Введите в ячейку Е15 формулу =(2-1)*(A9-1). 5. Рассчитайте фактический уровень значимости. 5.1. Выделите ячейку Е16. 5.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 5.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ТЕСТ> (рис. 46).
Р и с. 46
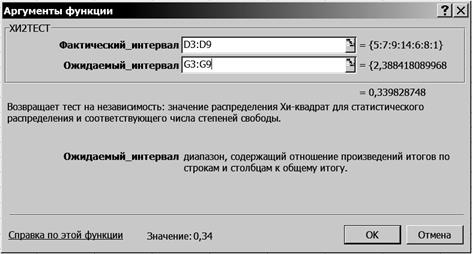
5.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 5.5. На вкладке ХИ2ТЕСТ установите параметры в соответствии с рис. 47.
Р и с. 47
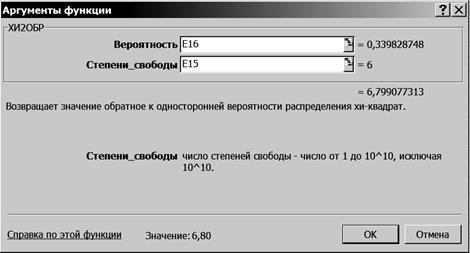
5.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 6. Рассчитайте фактическое значение критерия 6.1. Выделите ячейку Е17. 6.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 6.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ОБР> (рис. 48).
Р и с. 48
6.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 6.5. На вкладке ХИ2ОБР установите параметры в соответствии с рис. 49.
Р и с. 49 6.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 7. Определите табличное значение критерия Результаты решения выводятся на экран дисплея в следующем виде (рис. 50).
Р и с. 50
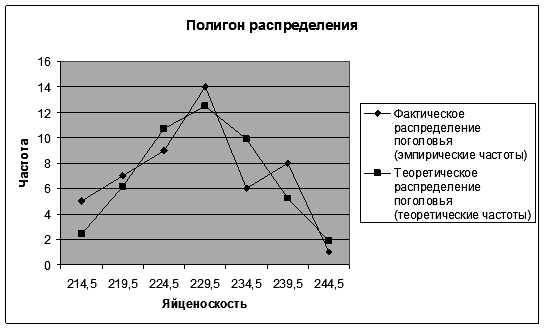
8. Постройте полигон фактического и теоретического распределения поголовья по яйценоскости. 8.1. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Мастер диаграмм > 8.2. В диалоговом окне Мастер диаграмм (шаг 1 из 4) с помощью левой кнопки мыши установите: Стандартные ® <График> (рис. 51).
Р и с. 51 8.3. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.4. В диалоговом окне Мастер диаграмм (шаг 2 из 4) установите параметры в соответствии с рис. 52.
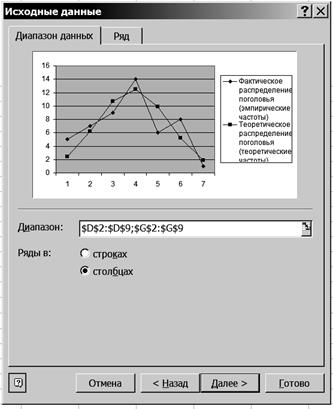
Р и с. 52 8.5. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.6. В диалоговом окне Мастер диаграмм (шаг 3 из 4) введите названия диаграммы и ос Y (рис. 53).
Р и с. 53
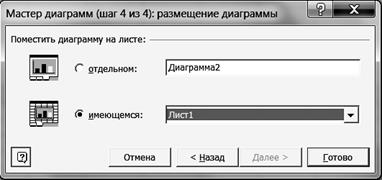
8.7. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.8. В диалоговом окне Мастер диаграмм (шаг 4 из 4) установите параметры в соответствии с рис. 54.
Р и с. 54
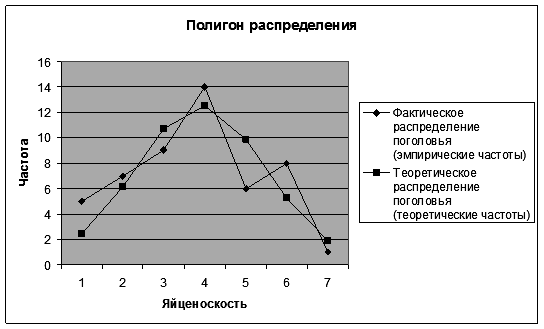
8.9. Щелкните левой кнопкой мыши на кнопке <Готово>. Результаты выводятся на экран дисплея в следующем виде (рис. 55).
Р и с. 55 9. Вставьте на графике подписи данных. 9.1. Щелкните правой кнопкой мыши на диаграмме и на появившейся вкладке нажмите кнопку <Исходные данные>. 9.2. В диалоговом окне Исходные данные измените подписи оси Х. Для этого выделите ячейки Е64:Е70 (рис. 56).
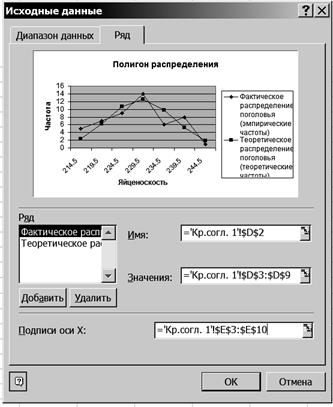
Р и с. 56 9.3. Нажмите клавишу <Enter>. Результаты выводятся на экран дисплея в следующем виде (рис. 57).
Р и с. 57
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 .
. .
. называют значение критерия, вычисленное по выборкам. Например, если по двум выборкам найдены исправленные выборочные дисперсии
называют значение критерия, вычисленное по выборкам. Например, если по двум выборкам найдены исправленные выборочные дисперсии  и
и  , то наблюдаемое значение критерия
, то наблюдаемое значение критерия  .
. называют точки, отделяющие критическую область от области принятия гипотезы.
называют точки, отделяющие критическую область от области принятия гипотезы. где
где  .
. , или равносильным неравенством
, или равносильным неравенством  .
. .
.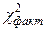 с табличным
с табличным  . Если
. Если 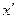
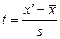
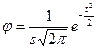

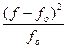
 и среднее квадратическое отклонение s;
и среднее квадратическое отклонение s;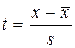 ;
;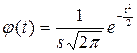 ,
, ,
, и
и 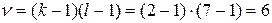 степенях свободы вариации равно 12,592 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).
степенях свободы вариации равно 12,592 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).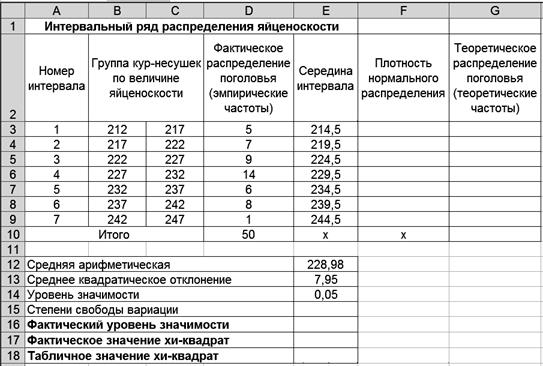
 или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.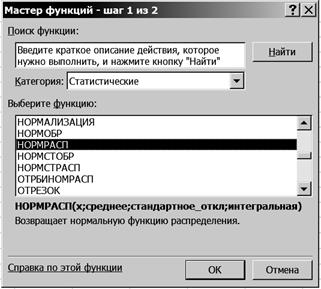
 .
.

 .
.