
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление критериев согласия Пирсона и КолмогороваСодержание книги
Поиск на нашем сайте
В критерии согласия Колмогорова в качестве показателя расхождения эмпирического и теоретического распределений используется число
где Коэффициенты l q распределяются по определенному закону и в зависимости от уровня значимости q имеют следующие значения:
В табл.3.1 в графах 4 и 5 приведены вероятности F (ti) и накопленные частоты Критерий согласия Колмогорова позволяет оценить принадлежность двух выборок одной и той же генеральной совокупности, для этого применяют показатель, вычисляемый по формуле где
3.3. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ
Если необходимо оценить однородность каких-либо процессов или явлений, другими словами, решить вопрос о принадлежности двух выборок одной генеральной совокупности, проверяют гипотезу о равенстве дисперсий. Как известно, точность измерений, изменчивость параметров залежей и показателей качества полезных ископаемых оценивается по степени рассеивания отдельных результатов относительно их центров. Мерой рассеивания является дисперсия. Сравнивая между собой дисперсии, мы можем решить задачу оценки равноточности или однородности результатов измерений, процессов или явлений. Гипотеза о равенстве дисперсий проверяется с помощью отношения
в числителе которого находится большее значение из двух независимо определенных выборочных дисперсий Это отношение подчиняется F -распределению Фишера – Снедекора, для которого в табл.3.2 для уровня значимости q = 0,05 приведены коэффициенты Fq, определяемые по двум значениям степеней свободы Гипотеза о равенстве дисперсий принимается, если соблюдается условие Таблица 3.2
F -распределение (q = 0,05)
3.4. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ
Допустим, имеется две выборки объемами N 1 и N 2 и известно, что они распределены нормально. Требуется определить, можно ли считать существенным расхождение в средних, вычисленных по каждой из этих выборок. В качестве критерия проверки гипотезы о равенстве средних двух выборок используется нормированная разность выборочных средних, вычисляемая по формуле
где Гипотеза о принадлежности исследуемых выборок одной генеральной совокупности принимается, если соблюдается условие
Использование гипотез о равенстве дисперсий и равенстве средних рассмотрим на примере ориентирования подземной полигонометрии. Так, гирокомпасом МВТ-2 пятикратно определен гироскопический азимут стороны полигонометрического хода двумя методами: с вычислением поправки за закручивание торсионного подвеса по шкале автоколлимационной трубы и по лимбу угломера. Получены следующие данные (приведены значения только минут):
Требуется установить, существенно или нет расхождение средних. Средние квадратические отклонения
3.5. ПРОВЕРКА СООТВЕТСТВИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ УСТАНОВЛЕННЫМ ДОПУСКАМ
На практике данная задача возникает в тех случаях, когда необходимо проверить, соответствует ли фактическая точность прибора или метода измерений установленным допускам. В этом случае сравнивают фактическую (выборочную) дисперсию и дисперсию, принимаемую в качестве допуска. Проверке подвергается число
где r – число степеней свободы; S – фактическая средняя квадратическая погрешность, полученная по результатам измерений; s – допустимая средняя квадратическая погрешность. Критерий согласия считается соблюденным или, другими словами, фактическая точность прибора, метода измерения линейных и угловых величин соответствует установленным допускам, если По невязке одного замкнутого подземного полигона средняя квадратическая погрешность измерения горизонтального угла S = 38². Требуется при уровне значимости q = 0,05 определить, допустима ли эта погрешность, если в качестве нормы установлена погрешность измерения угла в подземных условиях s = 20². В этом примере r = 1 (одно избыточное измерение – одна степень свободы). По формуле (3.8) находим Из обработки 10 замкнутых подземных полигонов одной шахты получена средняя квадратическая погрешность измерения горизонтального угла S = 28². При s = 20² определить, допустима ли эта погрешность. В этом случае r = 10. По формуле (3.8) находим
3.6. ОЦЕНКА СООТВЕТСТВИЯ ИЗМЕРЕННЫХ ПАРАМЕТРОВ ПРОЕКТНЫМ РАЗМЕРАМ
Данная задача имеет место в маркшейдерской практике при обслуживании проходки горных выработок и шахтном строительстве. Например, при проходке горных выработок маркшейдером контролируется соблюдение проектных параметров выработок по направлению, сечению и уклону. Выработка или часть ее, имеющая по маркшейдерским замерам отклонения от проектных размеров, бракуется. Основанием для этого является недопустимая разность между значением параметра выработки по маркшейдерским замерам и проектным значением. Аналогичная задача возникает при контроле полноты отработки полезного ископаемого. Например, размеры эксплуатационных потерь по руднику планируют ежегодно путем предрасчета ожидаемого значения по всем выемочным единицам. Полнота отработки контролируется сопоставлением плановых показателей извлечения и фактических, полученных на основании маркшейдерских замеров и съемок. Во всех рассматриваемых случаях сопоставляют средние, полученные на основании измерений, со средним проектным (плановым) значением. В данном случае проектный размер можно считать генеральной средней рассматриваемой совокупности, поскольку проектные параметры устанавливают с достаточно представительным обоснованием. Средний размер, полученный в процессе измерений, можно считать выборочным средним. Таким образом, статистическая задача сводится к установлению, принадлежит ли полученное нами выборочное среднее генеральной совокупности или нет. Если выборочное среднее в пределах точности его определения равно генеральному среднему, то делают вывод о принадлежности выборочного среднего генеральной совокупности. В противном случае гипотеза о подобном соответствии отвергается. В качестве критерия проверки принимают число
где Если различие между выборочным и генеральным средним носит случайный характер, т.е. данная выборка принадлежит генеральной совокупности, при q = 0,05 числа t распределяются по закону Стьюдента:
Если вычисленный по результатам замеров средний размер рассматриваемого параметра не соответствует проектному, то очевидно t ф > tq при заданном уровне значимости и числе степеней свободы r = N – 1. Рассмотрим на частном примере использование этого критерия. На год руднику установлены плановые потери полезного ископаемого 19,3 %, разубоживание 9,5 %. В отчетном году в работе было 11 очистных блоков. Среднее значение потерь, полученное на основе маркшейдерских замеров, 20,4 %, разубоживание 10,3 %. Относительные средние квадратические погрешности определения потерь равны 25 %, а разубоживания 20 %. Вычислим числа tф соответственно для потерь и разубоживания:
и
При уровне значимости q = 0,05 и числе степеней свободы r = 11 – 1 = 10 число tq = 2,23. Так как в обоих случаях t ф < tq, отклонение фактических показателей извлечения от плановых находится в пределах точности их определения.
4. ОСНОВЫ ДИСПЕРСИОННОГО АНАЛИЗА 4.1. ЗАДАЧИ ДИСПЕРСИОННОГО АНАЛИЗА
При геометризации месторождений полезных ископаемых, установлении допусков на горные работы, оценке равноточности маркшейдерских измерений и в целом ряде других случаев возникает необходимость определить влияние какого-либо фактора или группы факторов на значение изучаемого показателя, на характер процесса или явления. Например, при установлении допусков на проходку горных выработок обычно анализируют фактические отклонения параметров пройденных выработок от проекта. При этом следует полагать, что размеры этих отклонений могут зависеть от целого ряда причин: горно-геологических условий, технологии проходки, квалификации горнорабочих и т.д. Путем анализа степени влияния указанных причин размеры допусков устанавливают дифференцированно для различных условий. При этом возникает задача определения наличия и оценки степени влияния различных факторов на размеры отклонений параметров выработок от проекта. Для установления нормативов потерь и разубоживания полезных ископаемых при зачистке кровли и почвы пласта в карьере возникает необходимость проанализировать влияние на эти показатели таких факторов, как тип экскаватора, технология ведения буровзрывных работ. Подобных задач в маркшейдерском деле много. Когда взаимозависимые показатели заданы количественно, эти задачи могут быть решены методом корреляционного анализа. В том случае, когда факторы заданы качественно, используют метод дисперсионного анализа. 4.2. ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Сущность метода дисперсионного анализа рассмотрим для случая, когда на выраженный количественно нормально распределенный показатель x выявляется действие одного фактора. В такой постановке в математической статистике задача называется однофакторным дисперсионным анализом. Данные для анализа мы получаем из опыта, в процессе которого для различных типов (уровней) фактора Ф необходимо многократно определить показатель x. Например, разделив все образцы руд на литологические типы Ф j, отдельно для каждого типа определяют содержание изучаемого компонента xi. Результаты измерений группируют в виде матрицы наблюдений (табл.4.1). Будем считать, что число определений xi при каждом уровне фактора Ф j одинаково и равно p (i = 1, 2, …, p), число уровней фактора равно q (j = 1, 2, …, q). Вычислим общее среднее значение показателя:
а также средние значения, соответствующие каждому уровню фактора (групповые средние):
При отсутствии воздействия на показатель x фактора Ф различия между групповыми средними, а также их отличие от общего среднего должны носить случайный характер, т.е. с учетом случайной погрешности определения x должно соблюдаться равенство
Это рассеивание вызвано как действием на показатель x фактора Ф, так и другими причинами, которые в данном случае можно рассматривать как остаточные (или случайные) по отношению к фактору Ф.
Таблица 4.1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.68 (0.012 с.) |





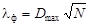 ; (3.3)
; (3.3)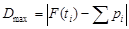 , (3.4)
, (3.4)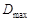 – максимальная разность накопленных частостей эмпирического распределения и вероятностей F (ti) теоретического распределения.
– максимальная разность накопленных частостей эмпирического распределения и вероятностей F (ti) теоретического распределения. , полученные по данным табл.1.1 (раздел 1.4.1). Максимальное значение разности, вычисленной по формуле (3.4) в графе 6, равно 0,01. Тогда
, полученные по данным табл.1.1 (раздел 1.4.1). Максимальное значение разности, вычисленной по формуле (3.4) в графе 6, равно 0,01. Тогда 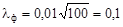 . Для уровня значимости q = 0,05 значение l q = 1,358. Поскольку lф < l q, гипотеза о соответствии эмпирического распределения нормальному закону подтверждается и по критерию Колмогорова.
. Для уровня значимости q = 0,05 значение l q = 1,358. Поскольку lф < l q, гипотеза о соответствии эмпирического распределения нормальному закону подтверждается и по критерию Колмогорова. , (3.5)
, (3.5) – максимальная разность между накопленными частостями выборок; N 1 и N 2 – объемы сравниваемых выборок.
– максимальная разность между накопленными частостями выборок; N 1 и N 2 – объемы сравниваемых выборок.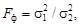 (3.6)
(3.6)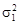 и
и  .
.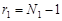 и
и  . Здесь N 1 и N 2 – объемы первой (большей) и второй выборок.
. Здесь N 1 и N 2 – объемы первой (большей) и второй выборок.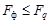 .
.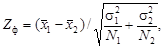 (3.7)
(3.7) и
и 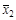 – эмпирические значения средних соответственно первой и второй сравниваемых выборочных совокупностей;
– эмпирические значения средних соответственно первой и второй сравниваемых выборочных совокупностей;  , где при заданном уровне значимости q коэффициент
, где при заданном уровне значимости q коэффициент  принимает следующие значения:
принимает следующие значения:
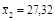
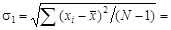
 , s2 = 0,421, разности средних
, s2 = 0,421, разности средних  . Показатель расхождения средних
. Показатель расхождения средних  . Поскольку при уровне значимости q = 0,05 значение
. Поскольку при уровне значимости q = 0,05 значение  , можно считать, что расхождение в средних значениях гироскопического азимута незначимо. Показатель расхождения дисперсий
, можно считать, что расхождение в средних значениях гироскопического азимута незначимо. Показатель расхождения дисперсий  . При q = 0,05 и r 1 = r 2 = 5 – 1 = 4 значение
. При q = 0,05 и r 1 = r 2 = 5 – 1 = 4 значение  (табл.3.2). Поскольку
(табл.3.2). Поскольку  , расхождение в дисперсиях тоже незначимо, поэтому обе рассматриваемые методики определения гироскопического азимута можно считать равноточными.
, расхождение в дисперсиях тоже незначимо, поэтому обе рассматриваемые методики определения гироскопического азимута можно считать равноточными. , (3.8)
, (3.8) (
( – критическая точка, выбираемая по числу степеней свободы
– критическая точка, выбираемая по числу степеней свободы  при уровне значимости q). Ниже приведены примеры использования рассмотренного критерия при анализе точностных характеристик измерений.
при уровне значимости q). Ниже приведены примеры использования рассмотренного критерия при анализе точностных характеристик измерений.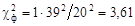 . По r = 1 и q = 0,05 определяем
. По r = 1 и q = 0,05 определяем 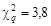 . Значение 3,61 < 3,8, следовательно, значение S = 38² не превосходит значимо допуск.
. Значение 3,61 < 3,8, следовательно, значение S = 38² не превосходит значимо допуск. . По r = 10 и q = 0,05 определяем значение
. По r = 10 и q = 0,05 определяем значение 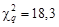 . Значение 19,6 > 18,3. Отсюда следует, что точность измерения углов на шахте превышает допуск.
. Значение 19,6 > 18,3. Отсюда следует, что точность измерения углов на шахте превышает допуск. , (3.9)
, (3.9)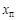 – проектное значение параметра;
– проектное значение параметра;  – средний размер, полученный из N измерений со средней квадратической погрешностью s каждого измерения.
– средний размер, полученный из N измерений со средней квадратической погрешностью s каждого измерения.
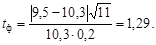

 (4.1)
(4.1)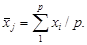 (4.2)
(4.2) . Степень рассеивания отдельных значений показателя
. Степень рассеивания отдельных значений показателя  относительно общего среднего
относительно общего среднего  (4.3)
(4.3)


