
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрица измеренных углов сдвиженияСодержание книги
Поиск на нашем сайте
Рассеивание измеренных значений xi от частных средних является результатом действия только случайных (остаточных) факторов, так как частные средние вычислены для одного и того же уровня рассматриваемых факторов, поэтому остаточная сумма квадратов отклонений
является характеристикой влияния на изменения показателя x остаточных факторов. По данным табл.4.3 S факт = 4(80 – 73,956)2 + 3(70 –73,956)2 + + 5(75 – 73,956)2 + 5(75 – 73,956)2 + 3(70,333 – 73,956)2 + 3(70 – – 73,956)2 = 290,3. В квадратных скобках помещены суммы квадратов отклонений измеренных значений xi от частных средних Вычислим факторную и остаточную дисперсии:
Поскольку Чтобы оценить воздействие на показатель x отдельно фактора A или фактора B, вычислим групповые (факторные) средние по уровням факторов A и B (табл.4.3): где nAi и nBi – сумма частот по каждому уровню факторов A и B. Контроль вычисления групповых средних:
Оценка воздействия каждого из рассматриваемых факторов на показатель x аналогична принципу однофакторного анализа. Показателем воздействия на величину x фактора A являются существенные различия в групповых средних
откуда SA = 187,7. Влияние на x фактора B характеризует сумма квадратов отклонений фактора B
тогда SB = 53,5. Вычислим дисперсии по факторам A и B:
тогда Определим по табл.3.2 случайные числа Fq -распределения. Для фактора A при q = 0,05, r 1 = d – 1 = 2, r 2 = N – pd = 17 значение FqA = 3,59; для фактора B при r 1 = p – 1 = 1 значение FqB = 4,45. Поскольку Контролем правильности вычислений сумм квадратов отклонений по факторам A и B будут являться следующие равенства:
где Суммы По данным табл.4.3
и
Следовательно, на углы сдвижения наиболее существенно влияют различия в горно-геологических условиях шахт.
5. ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ФУНКЦИЙ 5.1. ПОНЯТИЕ О СЛУЧАЙНОЙ ФУНКЦИИ В предыдущих разделах мы рассматривали совокупности случайных величин, полученные при определенных фиксированных условиях опыта. На практике учесть все условия опыта, как правило, невозможно. Опыт протекает во времени, в пространстве, при непрерывном действии посторонних причин, поэтому чаще приходится иметь дело со случайной величиной, непрерывно изменяющейся в процессе опыта. Например, произведем нивелировку откаточного пути в нескольких вариантах, в каждом из которых будут меняться расстояния между пикетами. Очевидно, при этом мы получим разные профили откаточного пути и разные высотные отметки в заданной точке профиля. Случайная величина здесь выступает в роли функции неслучайного параметра (интервала между пикетами), характеризующего условия опыта. Если случайной мы называли величину, которая в результате опыта принимала то или иное значение, причем не известное заранее, то по аналогии случайной функцией назовем такую, которая в результате опыта может принять тот или иной вид, причем заранее не известно, какой именно. Конкретный вид, принимаемый случайной функцией в результате опыта, называется реализацией случайной функции. Если аргументом случайной функции является время, то сама случайная функция, характеризующая процесс изменения случайной величины с течением времени, обычно называется случайным процессом. Если произвести ряд повторных опытов, то получим группу или семейство реализаций случайной функции. Таким образом, при n опытах мы получим n реализаций случайной функции. Если зададимся определенным значением аргумента, то ему будут соответствовать определенные значения случайной величины, число которых равно числу реализаций. Совокупность n случайных величин, отвечающих определенному значению аргумента случайной функции, называют сечением. Рассмотрим случайные функции одного аргумента – времени, обозначив его через t. Случайные функции будем обозначать прописными буквами латинского алфавита, а их реализации – соответствующими строчными. 5.2. ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНОЙ ФУНКЦИИ ИЗ ОПЫТА
Пусть проведено n независимых опытов и в результате получено n реализаций случайной функции Средним (математическим ожиданием) случайной функции называется неслучайная функция, выражающая зависимость средних
т.е. мы получили зависимость Дисперсией случайной функции называется неслучайная функция, выражающая зависимость от аргумента t дисперсий, вычисленных в каждом сечении по всем реализациям: для t 1
для t 2
для tj
для tm
Оценкой дисперсии случайной функции X (t) называют зависимость s2 = f (t). Ее можно также аппроксимировать каким-либо аналитическим выражением (см. раздел 2). Средним квадратическим отклонением случайной функции называется неслучайная функция, выражающая зависимость от аргумента t средних квадратических отклонений, вычисленных в каждом сечении по всем реализациям: для t 1
для t 2
для tj
для tm
Используя метод наименьших квадратов, зависимость s = f (t) можно также аппроксимировать каким-либо аналитическим выражением (см. раздел 2). Кроме того, если на графике 5.1 отложить полученные в сечениях значения ±s и провести через них линии, то в наглядном виде получим распределение средних квадратических отклонений математического ожидания Математическое ожидание и дисперсия – важные характеристики случайной функции, но для описания основных особенностей случайных функций этих характеристик недостаточно. Действительно, случайные функции X (t) и Y (t), изображенные на рис.5.2, имеют примерно одинаковые математические ожидания и дисперсии, однако характер изменения этих функций различен. Рассмотрим две ординаты случайной функции X (t) при значениях аргумента t = tj и t = tl, т.е. две случайные величины x (tj) и x (tl). Очевидно, что при близких значениях tj и tl величины x (tj) и x (tl) связаны тесной зависимостью: если величина x (tj) приняла какое-то значение, то и величина x (tl) с большой вероятностью примет значение близкое к нему. Очевидно и то, что по мере увеличения промежутка между tj и tl зависимость между случайными величинами x (tj) и x (tl) затухает очень медленно (рис.5.2, а).
Напротив, для случайной функции Y (t), изображенной на рис.5.2, б, ординаты y (tj) и y (tl) даже при близких значениях tj и tl практически не зависят друг от друга. Для такой случайной функции характерно быстрое затухание зависимости между ее ординатами при увеличении расстояния между ними. В качестве меры таких зависимостей используют корреляционный момент (ковариацию), вычисляемый для всех возможных пар аргументов tj и tl из m случайных величин (см. рис.5.1):
где n – число реализаций случайной функции. Зависимость Kx = f (t), полученную на основе вычисленных корреляционных моментов по формуле (5.1) для всех возможных пар соответствующих аргументов, называют оценкой корреляционной функции случайной функции X (t). За оценку нормированной корреляционной функции принимают зависимость
Нормированная корреляционная функция зависит от размера интервала аргумента D t. Для пар сечений, имеющих одинаковый интервал, вычисляют средние коэффициенты интервала. После определения достаточного числа значений эмпирической нормированной корреляционной функции r (D t) и построения графика обычно необходимо аппроксимировать функцию простым аналитическим выражением. Аппроксимирующее выражение должно отображать наиболее характерные свойства графика функции и сглаживать случайные колебания при больших значениях D t, т.е. в точках, полученных осреднением небольшого числа данных и поэтому ненадежных. Наиболее часто используют следующие аппроксимирующие выражения (рис.5.3):
Рассмотрим поведение функции Поведение функции
5.3. ПОНЯТИЕ О СТАЦИОНАРНОЙ СЛУЧАЙНОЙ ФУНКЦИИ На практике очень часто встречаются случайные функции, изменяющиеся во времени и пространстве примерно однородно, имеющие вид непрерывных случайных колебаний около некоторого постоянного среднего значения, причем ни средняя амплитуда, ни характер этих колебаний с течением времени не обнаруживает существенных изменений. К таким функциям можно отнести, например, колебания напряжений в электрической осветительной сети, случайные шумы в радиоприемнике, сезонные колебания земной поверхности, вызывающие случайный деформационный «шум» и т.д. Как правило, математическое ожидание такой случайной функции постоянно и не зависит от значения аргумента, а корреляционная функция зависит только от разности аргументов D t = t ¢ – t и не зависит от значений самих аргументов, т.е. выполняются следующие соотношения:
Kx (t, t ¢) = Kx (t ¢ – t) = Kx (D t). (5.6) Случайную функцию, математическое ожидание которой постоянно, а корреляционная функция зависит только от разности аргументов, называют стационарной в широком смысле. Поскольку дисперсия случайной функции равна ее корреляционной функции при t ¢ = t, учитывая соотношение (5.6), запишем следующую цепочку равенств:
Dx (t) = Kx (t, t ¢) = Kx (t ¢ – t) = Kx (0) = Dx = const, (5.7) т.е. дисперсия функции, стационарной в широком смысле, как и математическое ожидание, постоянна и не зависит от значения аргумента. В приведенное выше определение стационарности функции включены слова «в широком смысле», поскольку, вообще говоря, случайная функция X (t) называется стационарной относительно каких-либо характеристик, если эти характеристики не изменяются при любом сдвиге аргументов, от которых они зависят, по оси t (во времени). Иначе говоря, определенные характеристики инвариантны относительно любых сдвигов по t. В практических задачах случайные функции могут иметь различное количество характеристик, инвариантных относительно сдвигов вдоль оси времени (или оси аргументов в общем случае), поэтому можно говорить об их стационарности «в большей или меньшей степени». Заметим, что рассмотрение в качестве независимой переменной времени носит условный характер, аргумент случайной функции может иметь и другую природу. Стационарность в широком смысле представляет простейший вид стационарности. Для случайной функции, стационарной в широком смысле, только основные ее характеристики (математическое ожидание и корреляционная функция) не изменяются при любом сдвиге аргументов, от которых они зависят. Действительно, равенство (5.5) справедливо при всех допустимых значениях аргумента t, поэтому при сдвиге аргумента по оси t на промежуток D t математическое ожидание Другим крайним случаем является полная стационарность, или стационарность в узком смысле, когда все без исключения вероятностные характеристики случайной функции инвариантны относительно произвольных сдвигов по оси независимой переменной.
Нестационарная функция либо имеет изменяющееся с изменением аргумента математическое ожидание, т.е. нарушается равенство (5.5), либо ее корреляционная функция изменяется при сдвиге аргументов по оси t, т.е. нарушается равенство (5.6), либо нарушаются оба условия одновременно. Например, на рис.5.2, а изображена функция, математическое ожидание которой изменяется с течением времени. На рис.5.4 изображена функция с постоянным математическим ожиданием, но с изменяющейся с течением времени дисперсией, о чем свидетельствует увеличение с ростом аргумента отклонений реализаций случайной функции от математического ожидания. Заметим, что если случайная функция X (t) нестационарна только за счет переменного математического ожидания
Далее, в силу того, что корреляционный момент двух случайных величин совпадает с корреляционным моментом этих случайных величин, предварительно центрированных относительно их математических ожиданий (K [ X (t), X (t ¢)] = M {[ X (t) – M (X (t))] [ X (t ¢) – M (X (t ¢))]} = = M { X 0(t) X 0(t ¢)} = K [ X 0(t), X 0(t ¢)]), корреляционная функция K 0 x (t, t ¢) совпадает с корреляционной функцией Kx (t, t ¢) и, следовательно, как и Kx (t, t ¢), зависит только от разности аргументов: K 0 x (t, t ¢) = Kx (t, t ¢) = = Kx (t ¢ – t) = Kx (D t). Корреляционная функция любой случайной функции не меняет значения при перестановке значений аргументов, поэтому для стационарной случайной функции, учитывая соотношение (5.6), можно записать следующую цепочку равенств: Kx (D t) = Kx (t ¢ – t) = Kx (t, t ¢) = Kx (t ¢, t) = Kx (t – t ¢) = Kx (–D t), т.е. корреляционная функция стационарной случайной функции X (t) – четная функция разности аргументов. На практике вместо корреляционной функции Kx (D t) часто используют нормированную корреляционную функцию rx (D t) = Kx (D t)/ Dx. (5.8) Так как для стационарной случайной функции дисперсия Dx = const, то rx (D t) также четная, т.е. rx (D t) = rx (-D t). По смыслу rx (D t) при заданном D t есть коэффициент корреляции между ординатами случайной функции, разделенными по оси независимой переменной интервалом D t.
5.4. ЭРГОДИЧЕСКИЕ СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ Рассмотрим две стационарные случайные функции (рис.5.5). Каждая реализация случайной функции, изображенной на рис.5.5, а, обладает одними и теми же характерными признаками: средним уровнем, вокруг которого происходят колебания, и средним размахом этих колебаний относительно среднего уровня. Очевидно, что одна из таких произвольно выбранных реализаций сможет дать нам достаточно хорошее представление о свойствах случайной функции. Про случайную функцию, каждая реализация которой является как бы «полномочным представителем» всей совокупности возможных реализаций, говорят, что она обладает эргодическим свойством.
Рассмотрим случайную функцию, изображенную на рис.5.5, б. Очевидно, что средняя для каждой реализации может значительно отличаться от математического ожидания случайной функции. Про такую случайную функцию говорят, что она не обладает свойством эргодичности. Эргодическим свойством могут обладать и нестационарные случайные функции (см. рис.5.4).
5.5. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ЭРГОДИЧЕСКОЙ НЕСТАЦИОНАРНОЙ СЛУЧАЙНОЙ ФУНКЦИИ ПО ОДНОЙ РЕАЛИЗАЦИИ
Математическое ожидание нестационарной случайной функции можно определить сглаживанием одной ее реализации (рис.5.6), если полученная в результате опыта реализация случайной функции является достаточной по продолжительности и хорошо представляет всю совокупность возможных реализаций, т.е. рассматриваемая случайная функция обладает свойством эргодичности. Для сглаживания пользуются методом скользящей средней. За сглаженное значение функции в любой точке t принимают среднее значение в некотором интервале с центром в этой точке. При изменении t интервал скользит вдоль оси t, чем и объясняется название метода. Разобьем отрезок [0, T ] записи реализации случайной функции на равные части точками 0 = t 1, t 2, …, tk, …, tn = T. Для определения сглаженного значения функции в точке tk выделим из множества точек t 1, t 2, …, tn такое подмножество 2 p + 1 точек tk – p , …, tk – 1, tk, tk + 1, …, tk + p , в котором центральной точкой является точка tk. Сглаженное значение или, иначе говоря, значение скользящей средней ( 2 p + 1 )-го порядка в точке tk вычисляется по формуле
Используя формулу (5.9), можно вычислить сглаженные значения функции в точках tp + 1, tp + 2, …, tn-p. Очевидно, чем больше интервал, тем сильнее сглаживание. Но, с другой стороны, при очень большом интервале сгладится и само математическое ожидание случайной функции. Поэтому интервал рекомендуется выбирать таким, чтобы при любом его расположении внутри отрезка [0, T ] реализация случайной функции имела на нем достаточно большое количество колебаний и в то же время чтобы математическое ожидание случайной функции на интервале можно было считать приблизительно линейным. Оценку корреляционной функции нестационарной случайной функции по одной реализации можно получить, применяя метод скользящей средней к функции
рассматриваемой при фиксированном D t как функцию от t. В формуле (5.10) функция Допустим, что сглаживание реализации x (t) случайной функции проводилось скользящей средней (2 p + 1)-го порядка. Разобьем отрезок записи реализации случайной функции на равные части длиной h точками 0 = t 1, t 2, …, tn = T. Тогда оценкой значения корреляционной функции Kx (D t) в точке D t = mh, где m = 1, 2, …, n, является скользящая средняя, вычисленная по следующей совокупности чисел:
………………………………………………………….
6. ФРАКТАЛЬНЫЙ АНАЛИЗ
6.1. ФРАКТАЛЫ И ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ Фрактальная геометрия и фрактальный анализ – сравнительно новая область науки, заявившая о себе после опубликования фундаментальных трудов Б.Мандельброта, который показал, что геометрия большинства природных объектов допускает, кроме характеристики традиционными геометрическими понятиями, также описание фрактальными объектами, части которых в какой-то степени подобны целому. Согласно Б.Мандельброту, «…многие формы, которые до сих пор характеризовались как зернистые, гидроподобные, похожие на морские водоросли, странные, запутанные, ветвистые, ворсистые, морщинистые и т.п., могут отныне изучаться и записываться в строгих количественных терминах» [3, с.19]. В 1975 г. Бенуа Мандельброт ввел термин «фрактал» от латинского слова fractus, которое означает «ломаный», «разбитый». Однако только после опубликования в 1983 г. Б.Мандельбротом «Фрактальной геометрии природы» («The fractal geometry nature») понятие о фракталах вошло в другие науки и стало основой для рассмотрения различных окружающих нас природных форм. Оказалось, что фракталы дают необычно компактный способ описания объектов и процессов [3]. Традиционные методы горной геометрии основаны на приближенной аппроксимации сложных форм горно-геологических объектов геометрическими фигурами: точками, прямыми, отрезками, плоскостями, многоугольниками и т.д., – метрические и топологические размерности которых равны между собой. При этом, когда речь идет о геометризации геологических структур (геометризация месторождений полезных ископаемых), часть информации об объектах утрачивается, так как распределение квалиметрических характеристик залежи усредняется и форма геологической структуры искусственно упрощается. Фрактальная геометрия, оперирующая дробными метрическими размерностями исследуемых объектов, не только характеризует их геометрический образ, но и отражает процессы образования и эволюции, что является важным. Многие сложные структуры обладают фундаментальным свойством геометрической регулярности – инвариантностью по отношению к масштабу, или «самоподобием». При рассмотрении таких структур с различным увеличением обнаруживается, что одни и те же элементы строения повторяются на каждом масштабном уровне. Эти закономерности повторения определяют дробную, или фрактальную, размерность структуры. При этом, по-видимому, фрактальная геометрия описывает природные объекты точнее и проще, чем евклидова геометрия. Различают геометрические, или регулярные, фракталы (множество Кантора, кривые Коха, треугольник и ковер Серпинского и др.) и нерегулярные и природные фракталы (полимеры, облака, пористые среды и т.д.)
6.2. ГЕОМЕТРИЧЕСКИЕ ФРАКТАЛЫ И ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому [9]. Размерность в топологии определяется количеством пространственных измерений или степенью многомерности. В евклидовом пространстве RE размерность Dt является целым числом и заключена в промежутке от 0 до Е. Евклидова размерность Dt для точки равна 0, для линии 1, для плоскости 2 и для трехмерных фигур 3. Но если точки расположены достаточно часто, то при определенном масштабе рассмотрения они сольются в линию. Если линия сильно извивается, то она покрывает собой какую-то площадь. Следовательно, размерность таких объектов должна быть дробной, или фрактальной. При непосредственном наблюдении фрактальных объектов составляющие их основные элементы недоступны рассмотрению. Фракталы выражаются в алгоритмах, наборах математических процедур. Обычно эти алгоритмы преображаются в геометрические образы с помощью компьютерной программы. Собственно и становление фрактальной геометрии и анализа стало возможным при развитии компьютерных технологий. Таким образом, геометрические, или регулярные, фракталы строятся методом итераций с бесконечным количеством шагов. Классическими примерами таких объектов являются кривые Коха, множество Кантора, треугольник и ковер Серпинского [3]. Рассмотрим некоторые из них.
Кривая Коха (рис.6.1) получается путем преобразования единичного отрезка прямой линии (нулевой шаг построения, n = 0, рис.6.1, а) в ломаную по определенным правилам. Для построения триадной кривой Коха этот отрезок на первом шаге (n = 1) делится на три равные части с длиной d = 1/3 первоначального отрезка и центральная часть надстраивается двумя равными d отрезками наподобие сторон угла (рис.6.1, б). На следующем шаге (n = 2) эта операция повторяется над всеми прямолинейными звеньями предыдущего шага (рис.6.1, в) и так далее до бесконечности. В результате получим серию кривых с n = 1, 2, 3 … и длиной звеньев d = 3-1, 3-2, 3-3 … и т.д. На первом шаге кривая состоит из четырех прямолинейных отрезков, каждый длиной 1/3 первоначального, т.е. из четырех отрезков, подобных исходному, с коэффициентом подобия 1/3. Тогда длина всей кривой первого поколения будет L (1/3) = 4/3 первоначальной длины, а второго L (1/9) = (4/3)2 = 16/9. Кривая n -го поколения будет иметь длину звена d = 3- n , которое связано с шагом построения соотношением
Фрактальная размерность для фракталов является дробным числом и в случае с кривой Коха выражает степень приращения длины линии, или ее «толщину». Эту ломаную линию можно вытянуть в прямую, поэтому топологическая размерность кривой Коха Dt = 1, т.е. отвечает топологической поверхности прямой линии, а фрактальная размерность Д = ln4/ln3 = 1,2628 …, т.е. кривая Коха есть фрактальное множество с Д = 1,263 [3]. При бесконечном количестве шагов построения полученная линия обладает совершенно удивительным свойством. Имея начало и конец, она, тем не менее, обладает бесконечной длиной. Кроме того, она ни в одной точке не имеет производной, так как при бесконечном продолжении процесса каждая ее точка в какой-то момент станет угловой, а в точке углового соединения прямых производной не существует. Рассматривая эту кривую в сколь угодно малый микроскоп, мы всегда будем видеть одно и то же, т.е. кривая инвариантна относительно масштаба. Последнее свойство называется самоподобием и является основным свойством геометрических самоподобных фракталов. Множество Кантора (рис.6.2). В практике для анализа естественно образующихся фрактальных структур часто используются канторовские множества. Рассмотрим их построение на примере триадного множества Кантора (рис.6.2). Возьмем единичный отрезок (рис.6.2, а) и разделим его на три равные части, а затем среднюю часть выбросим (рис.6.2, б) Повторим эту операцию для каждого полученного отрезка (рис.6.2, в, г). В результате деления при бесконечно большом числе поколений получим бесконечное множество точек, рассеянное по единичному отрезку («канторовская пыль»). На первом шаге мы получили два отрезка длиной 1/3 первоначальной длины каждый. Тогда общая длина образующихся отрезков составит L (1/3) = 2/3, а на втором шаге L (1/9) = (2/3)2 = 4/9.
Таким образом, общая длина отрезков на n -м шаге
а фрактальная размерность Д = ln2/ln3 = 0,6390. Так как 0 < Д < 1, полученное множество можно рассматривать либо как плотно расположенные точки, либо как очень дырявую прямую. И здесь вид множества будет зависеть от масштаба рассмотрения, от того, какого размера дырки «чувствует» микроскоп. Топологическая размерность такого множества Dt = 0. Поскольку число Д дробное и Д > Dt, можно заключить, что триадное канторовское множество есть фрактальное множество [3]. Оно также будет самоподобным в силу постоянства коэффициента деления и выбрасывания. Построение двух приведенных регулярных фракталов производилось по определенным правилам, т.е. каждый последующий шаг был заранее определен. Поэтому их называют детерминированными или регулярными фракталами. Детерминированные фракталы могут быть построены в одно-, двух-, трех- и более мерном пространстве из точек, линий, различных фигур. Они имеют постоянный способ перехода от шагу к шагу и, соответственно, постоянное приращение на каждом шаге количества точек, длины, площади, объема. Именно динамику этого приращения и характеризует фрактальная размерность Д. Таким образом, Д – это дробное число, характеризующее степень изрезанности контура или сложность структуры. Исходную фигуру, из которой строится фрактал, называют инициатором или «заставкой», а способ перехода от шага к шагу – генератором или образующим элементом. В двух рассмотренных выше регулярных фракталах применялся один и тот же генератор. Можно использовать разные генераторы на каждом последующем шаге. Но для того, чтобы полученный объект был фракталом, необходимо использовать генераторы с одной и той же фрактальной размерностью.
6.3. НЕРЕГУЛЯРНЫЕ И ПРИРОДНЫЕ ФРАКТАЛЫ
Приведенные выше примеры регулярных фрак
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.252 (0.018 с.) |

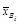
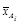
 ; в квадратных
; в квадратных 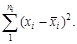
 (4.12)
(4.12)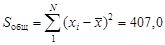 . Контролем правильности вычислений сумм квадратов отклонений служит равенство (4.4): 290,3 + 116,7 = 407,0.
. Контролем правильности вычислений сумм квадратов отклонений служит равенство (4.4): 290,3 + 116,7 = 407,0.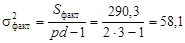 ;
; .
.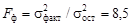 и больше Fq = 2,8, при q = 0,05,
и больше Fq = 2,8, при q = 0,05, 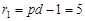 и
и 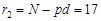 (см. табл.4.3) можно говорить о том, что горно-геологические условия шахт и повторность подработки оказывают существенное влияние на углы сдвижения: k д = (290,3:407,0)100 = 71,3 % от всех других возможных причин.
(см. табл.4.3) можно говорить о том, что горно-геологические условия шахт и повторность подработки оказывают существенное влияние на углы сдвижения: k д = (290,3:407,0)100 = 71,3 % от всех других возможных причин.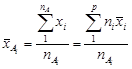 ;
;  , (4.13)
, (4.13)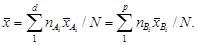
 , а также их существенное отличие от общего среднего. Характеристикой этого является сумма квадратов отклонений фактора A
, а также их существенное отличие от общего среднего. Характеристикой этого является сумма квадратов отклонений фактора A , (4.14)
, (4.14)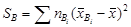 , (4.15)
, (4.15) ;
; ,
,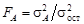 = 93,8: 6,9 = 13,6;
= 93,8: 6,9 = 13,6; 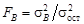 = 53,5: 6,9 = 7,8.
= 53,5: 6,9 = 7,8.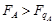 ,
, 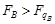 , каждый из рассматриваемых факторов существенно влияет на углы сдвижения.
, каждый из рассматриваемых факторов существенно влияет на углы сдвижения. ; (4.16)
; (4.16)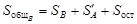 , (4.17)
, (4.17)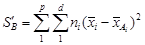 ;
; 
 и
и 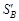 характеризуют рассеивание частных средних относительно групповых средних. Например, рассеивание частных средних
характеризуют рассеивание частных средних относительно групповых средних. Например, рассеивание частных средних  фактора B.
фактора B. = 4(80 – 75,417)2 + 3(70 – 75,417)2 + 5(75 – 75,417)2 + + 5(75 – 75,364)2 + 3(70,333 – 72,364)2 + 3(70 – 72,364)2 = 236,8. Контроль: S общ А = 187,7 + 102,6 + 116,7 = 407,0; S общ В = 53,5 + 236,8 + + 116,7 = 407,0. Коэффициенты детерминации по факторам A и B соответственно
= 4(80 – 75,417)2 + 3(70 – 75,417)2 + 5(75 – 75,417)2 + + 5(75 – 75,364)2 + 3(70,333 – 72,364)2 + 3(70 – 72,364)2 = 236,8. Контроль: S общ А = 187,7 + 102,6 + 116,7 = 407,0; S общ В = 53,5 + 236,8 + + 116,7 = 407,0. Коэффициенты детерминации по факторам A и B соответственно
 .
. (рис.5.1). Найдем оценки характеристик случайной функции: математического ожидания, дисперсии и корреляционной функции.
(рис.5.1). Найдем оценки характеристик случайной функции: математического ожидания, дисперсии и корреляционной функции.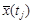 из числа реализаций в каждом сечении от аргумента t (рис.5.1). Для t 1, t 2 и tj соответственно
из числа реализаций в каждом сечении от аргумента t (рис.5.1). Для t 1, t 2 и tj соответственно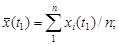
 и
и 
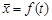 , которую можно аппроксимировать каким-либо аналитическим выражением, используя, например, метод наименьших квадратов (см. раздел 2). Зависимость
, которую можно аппроксимировать каким-либо аналитическим выражением, используя, например, метод наименьших квадратов (см. раздел 2). Зависимость 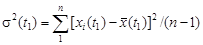 ,
,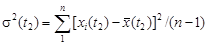 ,
,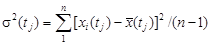 ,
, .
.
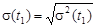 ,
, ,
,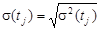 ,
,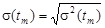 .
.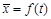 случайной функции X (t). Неслучайная функция s = f (t), так же как и в предыдущих случаях, носит название оценки среднего квадратического отклонения случайной функции X (t).
случайной функции X (t). Неслучайная функция s = f (t), так же как и в предыдущих случаях, носит название оценки среднего квадратического отклонения случайной функции X (t).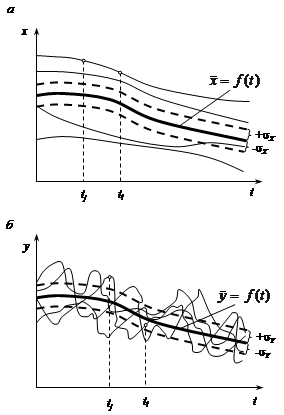
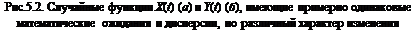
 , (5.1)
, (5.1) , т.е. зависимость между возможными парами аргументов и выборочными нормированными корреляционными моментами, или, иначе говоря, выборочными коэффициентами корреляции соответствующих ординат. Выборочный коэффициент корреляции случайных величин (нормированный корреляционный момент) для пары аргументов tj и tl находят по формуле
, т.е. зависимость между возможными парами аргументов и выборочными нормированными корреляционными моментами, или, иначе говоря, выборочными коэффициентами корреляции соответствующих ординат. Выборочный коэффициент корреляции случайных величин (нормированный корреляционный момент) для пары аргументов tj и tl находят по формуле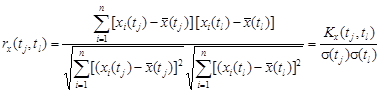 . (5.2)
. (5.2)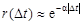 ; (5.3)
; (5.3)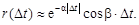 (5.4)
(5.4)
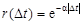 при изменении a. При уменьшении a функция r (D t) убывает медленнее и, следовательно, характер изменения случайной функции более плавный. При увеличении a функция r (D t) убывает быстрее и характер колебания случайной функции более резкий и беспорядочный.
при изменении a. При уменьшении a функция r (D t) убывает медленнее и, следовательно, характер изменения случайной функции более плавный. При увеличении a функция r (D t) убывает быстрее и характер колебания случайной функции более резкий и беспорядочный. зависит от соотношения параметров a и b, т.е. от того, что преобладает в корреляционной функции: убывание по закону
зависит от соотношения параметров a и b, т.е. от того, что преобладает в корреляционной функции: убывание по закону 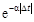 или колебание по закону
или колебание по закону 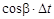 . Очевидно, при сравнительно малых значениях a преобладает колебание, при сравнительно больших – убывание.
. Очевидно, при сравнительно малых значениях a преобладает колебание, при сравнительно больших – убывание. (5.5)
(5.5)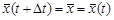 , т.е. оно инвариантно относительно любого сдвига аргумента по оси t. Равенство (5.6) справедливо при всех допустимых значениях аргументов t и t ¢. Дадим обоим аргументам приращение D t. Тогда Kx (t + D t, t ¢ + D t) = = Kx (t ¢ + D t – t – D t) = Kx (t ¢ – t) = Kx (t, t ¢), т.е. и корреляционная функция инвариантна относительно любого сдвига аргументов по оси t. Требование стационарности в широком смысле накладывает на случайную функцию наименьшие ограничения.
, т.е. оно инвариантно относительно любого сдвига аргумента по оси t. Равенство (5.6) справедливо при всех допустимых значениях аргументов t и t ¢. Дадим обоим аргументам приращение D t. Тогда Kx (t + D t, t ¢ + D t) = = Kx (t ¢ + D t – t – D t) = Kx (t ¢ – t) = Kx (t, t ¢), т.е. и корреляционная функция инвариантна относительно любого сдвига аргументов по оси t. Требование стационарности в широком смысле накладывает на случайную функцию наименьшие ограничения.
 , то вместо X (t) следует рассмотреть случайную функцию X 0(t) = X (t) –
, то вместо X (t) следует рассмотреть случайную функцию X 0(t) = X (t) – 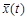 , которая удовлетворяет условиям стационарности. Действительно, ее математическое ожидание постоянно и равно нулю:
, которая удовлетворяет условиям стационарности. Действительно, ее математическое ожидание постоянно и равно нулю: .
.

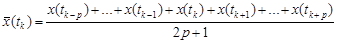 . (5.9)
. (5.9) , (5.10)
, (5.10) – сглаженная реализация соответственно на отрезке [0, T – D t ] и [D t, T ].
– сглаженная реализация соответственно на отрезке [0, T – D t ] и [D t, T ]. ;
;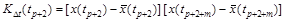 ;
; .
.

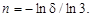
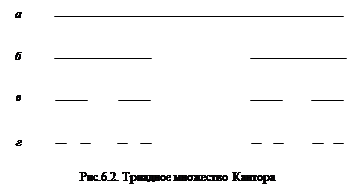
 ,
,


