
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрица наблюдений однофакторного анализаСодержание книги
Поиск на нашем сайте
Для характеристики изменения показателя x, вызванного действием фактора Ф, разложим общую сумму квадратов отклонений S общ на факторную и остаточную составляющие:
где Поскольку
Общая, остаточная и факторная дисперсии соответственно
Если на изучаемый показатель не действует фактор Ф, должно соблюдаться условие
Число степеней свободы для факторной дисперсии вычисляют по формуле Если на показатель x будет влиять фактор Ф, дисперсия Например, требуется установить влияние различных типов теодолитов (уровни фактора) на точность измерения угла. Были исследованы три теодолита, каждым из которых четырежды измерен один и тот же угол. Полученные значения углов различались только в секундах, поэтому в матрице наблюдений (табл.4.2) приведена только эта часть данных.
Таблица 4.2 Результаты измерения углов
Для упрощения вычислений можно от каждого значения угла отнять, например, 52². Полученные условные значения в табл.4.2 приведены в скобках. Дальнейшие вычисления выполняют, используя условные значения. Условное общее среднее
4.3. ОЦЕНКА СТЕПЕНИ ВЛИЯНИЯ ФАКТОРОВ Как уже говорилось, S общ = S ост + S факт. Разделим это выражение на объем выборки N. Известно, что s2 = S / N. Тогда равенство сумм квадратов можно записать в следующем виде:
По определению
Следовательно, действие всех факторов на исследуемый показатель можно представить в виде суммы квадратов корреляционных отношений (или коэффициентов корреляции при линейной связи). Квадрат корреляционного отношения, выраженный в процентах, называют поэтому коэффициентом детерминации, т.е.
Для вычисления коэффициентов детерминации используем данные примера раздела 4.2 и табл.4.2: S общ = 266, S факт = 152, S ост = 114. Тогда k д.факт = (152: 266)100 = 57 %; k д.ост = (114: 266)100 = = 43 %. Следовательно, отклонения отдельных значений от среднего на 57 % обусловлены различными типами теодолитов.
4.4. ДВУХФАКТОРНЫЙ АНАЛИЗ
Если изучают влияние на величину x двух и более факторов, то принцип решения задачи анализа остается таким же, как и при однофакторном, усложняются лишь вычисления. Рассмотрим технику вычислений при двухфакторном анализе для общего случая, когда число определений показателя на каждом уровне факторов различное. Например, на трех разных шахтах были многократно измерены углы сдвижения по простиранию пласта при первичной и повторной подработках (табл.4.3). С использованием метода дисперсионного анализа необходимо установить, влияют ли различия в горно-геологических условиях шахт, а также повторность подработки на углы сдвижения. В матрице наблюдений (табл.4.3) измеренные значения углов сдвижения xi (в градусах) размещены в клетках таблицы соответственно числу подработок (первичная или повторная, уровни pi фактора B) раздельно для каждой из трех шахт (уровни di фактора A). Общее среднее
Качественной оценкой совместного влияния на углы сдвижения факторов A и B является сравнение вычисленных частных средних
Если принять, что случайные факторы отсутствуют, а факторы A и B не оказывают влияния на показатель x, то
Таблица 4.3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |








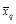

 (4.4)
(4.4) – остаточная сумма квадратов отклонений S ост, которая характеризует рассеивание отдельных значений относительно средних по уровням (групповых средних) и не зависит от действия фактора Ф;
– остаточная сумма квадратов отклонений S ост, которая характеризует рассеивание отдельных значений относительно средних по уровням (групповых средних) и не зависит от действия фактора Ф;  – факторная сумма квадратов отклонений S факт, так как изменение средних по уровням фактора при достаточной представительности результатов измерений должно в основном определяться действием фактора Ф.
– факторная сумма квадратов отклонений S факт, так как изменение средних по уровням фактора при достаточной представительности результатов измерений должно в основном определяться действием фактора Ф. , сумма
, сумма  . Следовательно, общая сумма квадратов отклонений
. Следовательно, общая сумма квадратов отклонений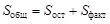 . (4.5)
. (4.5) ;
;  ;
;  . (4.6)
. (4.6) , так как степень рассеивания групповых средних относительно общего среднего не должна быть больше, чем отдельных значений относительно групповых средних. Но может оказаться, что
, так как степень рассеивания групповых средних относительно общего среднего не должна быть больше, чем отдельных значений относительно групповых средних. Но может оказаться, что  . Это может быть вызвано или влиянием фактора Ф, или влиянием остаточных факторов. В качестве показателя существенности различия дисперсий используют безразмерную величину
. Это может быть вызвано или влиянием фактора Ф, или влиянием остаточных факторов. В качестве показателя существенности различия дисперсий используют безразмерную величину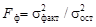 . (4.7)
. (4.7) , а остаточной – по формуле
, а остаточной – по формуле  .
. будет существенно превышать
будет существенно превышать  , а следовательно, фактическое отношение этих дисперсий должно быть больше случайных чисел F -распределения. Поэтому при
, а следовательно, фактическое отношение этих дисперсий должно быть больше случайных чисел F -распределения. Поэтому при  можно утверждать, что на исследуемый показатель влияет фактор Ф. В противном случае, когда
можно утверждать, что на исследуемый показатель влияет фактор Ф. В противном случае, когда  , влияние на x фактора Ф отвергается.
, влияние на x фактора Ф отвергается. = (–1 + 0 + + 4 + 5 + 0 + 2 + 4 + 6 – 10 – 8 – 2 + 0): 12 = 0; групповые средние
= (–1 + 0 + + 4 + 5 + 0 + 2 + 4 + 6 – 10 – 8 – 2 + 0): 12 = 0; групповые средние  = (–1 + 0 + 4 + 5): 4 = 2;
= (–1 + 0 + 4 + 5): 4 = 2;  = (0 + 2 + 4 + 6): 4 = 3;
= (0 + 2 + 4 + 6): 4 = 3; 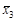 = (–10 – 8 – – 2 + 0): 4 = –5. Факторная сумма квадратов отклонений S факт = = 4 [(2 – 0)2 + (3 – 0)2 + (–5 – 0)2] = 152; дисперсия
= (–10 – 8 – – 2 + 0): 4 = –5. Факторная сумма квадратов отклонений S факт = = 4 [(2 – 0)2 + (3 – 0)2 + (–5 – 0)2] = 152; дисперсия  рассматриваемые типы теодолитов имеют различную точность измерения угла.
рассматриваемые типы теодолитов имеют различную точность измерения угла. или
или . (4.8)
. (4.8) или
или  (см. раздел 2.6). Тогда выражение (4.8) можно записать так:
(см. раздел 2.6). Тогда выражение (4.8) можно записать так:  или в процентах
или в процентах . (4.9)
. (4.9) . (4.10)
. (4.10) (где N – число всех измерений равное 23). В каждой клетке таблицы вычислим частные средние
(где N – число всех измерений равное 23). В каждой клетке таблицы вычислим частные средние  , соответствующие определенным уровням факторов A и B, по формуле
, соответствующие определенным уровням факторов A и B, по формуле  (где ni – число измеренных углов сдвижения в каждой клетке таблицы, соответствующее определенным уровням факторов A и B). Значения
(где ni – число измеренных углов сдвижения в каждой клетке таблицы, соответствующее определенным уровням факторов A и B). Значения 
 . Во-вторых, случайными причинами (на фоне рассматриваемых факторов): погрешность измерения, разная представительность выборок, другие не учитываемые в данном случае факторы. Очевидно, что характеристикой влияния на показатель x факторов A и B является факторная сумма квадратов отклонений
. Во-вторых, случайными причинами (на фоне рассматриваемых факторов): погрешность измерения, разная представительность выборок, другие не учитываемые в данном случае факторы. Очевидно, что характеристикой влияния на показатель x факторов A и B является факторная сумма квадратов отклонений (4.11)
(4.11)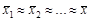 и
и  .
.


