
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление вероятностей невязокСодержание книги Поиск на нашем сайте
Гусев В.Н. Г96. Математическая обработка маркшейдерской информации статистическими методами: Учеб. пособие / В.Н.Гусев, А.Н.Шеремет. Санкт-Петербургский государственный горный институт (технический университет). СПб, 2005.98 с. ISBN 5-94211-144-8
УДК 519.2:622(075.80) ББК 33.12
Введение
Настоящий курс математической обработки результатов различного рода маркшейдерских измерений методами математической статистики предназначен для студентов специальности 090100 «Маркшейдерское дело». Поскольку статистические методы и подходы к решению различных технических задач, связанных с обработкой и анализом большого объема статистической информации, универсальны, изложенный материал может быть полезен для студентов геологических и горно-технологических специальностей. Содержание пособия соответствует образовательному стандарту курса «Математическая обработка результатов измерений» специальности 090100. В маркшейдерском деле статистическая информация обычно представлена в виде различного рода показателей геомеханических свойств горных пород и процессов, горно-геометрических показателей, характеризующих структурные особенности пород, качественных показателей полезного ископаемого, пород, результатов маркшейдерско-геодезических измерений, съемок. Количество такой информации носит массовый характер. Это вызывает необходимость систематизации и обработки результатов таким образом, чтобы они достаточно полно отражали свойства изучаемого процесса или объекта и вместе с тем были удобными для практического использования. Такого рода задачи оптимально решаются методами математической статистики. В учебном пособии затронуты такие вопросы, как определение параметров распределения статистических показателей, теоретические законы распределения, подбор их под эмпирические зависимости с оценкой через проверку гипотез степени соответствия фактически получаемым распределениям. Рассмотрены вопросы корреляционного анализа, включая вопросы множественной корреляции, приведение нелинейных зависимостей к линейному виду. Затронуты вопросы применения методов статистической проверки гипотез, используемых как при оценке результатов измерений, так и при оценке и выводе корреляционных связей. Отдельно рассмотрены вопросы использования методов дисперсионного анализа при решении горно-геометрических, сдвиженческих и других задач маркшейдерского дела. В общем виде рассмотрены методы оценки процессов на основе теории случайных функций. Отдельная глава посвящена методам фрактального анализа для оценки степени изменчивости получаемой статистической информации при геометризации недр.
1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЗАКОНА РАСПРЕДЕЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И ГОРНО-ГЕОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ
1.1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ВЫБОРКИ
Случайной величиной обычно называют такую, которая в результате опыта может принимать то или иное значение, не известное нам заранее в пределах требуемой точности ее определения. Случайные величины бывают дискретными и непрерывными. Дискретные (прерывные) величины, принимающие конечные счетные значения (число скважин, встретивших полезное ископаемое; число лав, отрабатываемых в данный период на шахте; число трещин на определенном интервале исследования и др.). Непрерывные величины принимают в некоторых пределах любые значения. Содержание полезного компонента в рудном теле может принимать любые значения от минимального до максимального для данной залежи и типа полезного ископаемого; погрешности измерений могут непрерывно изменяться от нуля до некоторого предела, зависящего от точности измерений, типа измерительного прибора, субъективного фактора. Численные значения случайных величин получают в процессе опыта, в качестве которого могут выступать маркшейдерские съемки, разведка и опробование залежи, опробование полезного ископаемого, определение различного рода показателей производственной деятельности горно-добывающего предприятия, изучение распределения горно-геометрических иквалиметрических показателей недр, геомеханические показатели процесса сдвижения и деформаций горных пород и др. Определенное количество значений случайной величины, характеризующее изучаемый процесс или объект, называют совокупностью, а число этих значений в совокупности – ее объемом. Весь набор множества однородных показателей, характеризующих исследуемый объект или процесс, называют генеральной совокупностью. При больших объемах генеральной совокупности объекты или явления изучают путем извлечения из нее части показателей, которую называют выборочной совокупностью или выборкой. Чтобы по данным выборки можно было с достаточной надежностью оценить изучаемую генеральную совокупность, выборка должна удовлетворять требованию представительности (репрезентативности), что обеспечивают применением соответствующих способов отбора значений показателей и объемов выборки. Различают следующие способы отбора показателей выборки: случайный, механический, типический, серийный, комбинированный. В случайном способе данные отбирают с привлечением случайных чисел; этот способ применяется, если не удается установить предварительно какие-либо закономерности поведения показателя в генеральной совокупности (в маркшейдерском деле этот способ почти не используется). В механическом способе генеральная совокупность «механически» делится на равные части и в каждой из них определяется по одному значению показателя. Способ широко используется в маркшейдерском деле, например, при замерах сечений горных выработок через определенные интервалы, при замерах систем трещин и качественном опробовании полезного ископаемого и вмещающих пород также через определенные интервалы. Применению данного способа должно предшествовать выявление оптимального размера элементарной части (интервала), в котором определяют значения показателя. В типическом способе изучаемую генеральную совокупность предварительно делят на различные типы и определяют значения показателя для каждого типа отдельно (разделение залежи полезного ископаемого на типы руд, категории запасов; разделение выработок по назначению, креплению, горно-геологическим условиям проходки). В серийном способе из генеральной совокупности отбирают не отдельные значения, а «серии» значений, при этом показатели каждой серии подвергают сплошному определению (такой способ применяют при контроле качества продукции). Комбинированный способ представляет собой сочетание вышеприведенных способов. Часто используют сочетание типического и механического способов формирования выборки при опробовании месторождений. Заметим, что приведенные способы отбора показателей выборки являются элементами планирования эксперимента и исследовательских работ.
1.2. ВАРИАЦИОННЫЙ РЯД
Пусть выборка представлена объемом, исчисляемым тысячами значений определяемого показателя. В этом случае для удобства их использования, анализа и получения практических выводов пользуются вариационным (статистическим, сгруппированным) рядом распределения значений показателя. Вариационный ряд для дискретных случайных величин составляется следующим образом. Пусть из генеральной совокупности извлечена выборка объемом N. В этом объеме значения показателя x 1, x 2, …, xk называются вариантами, а объем каждого варианта n 1, n 2, …, nk – его частотой. Записав полученную выборку по возрастанию численных значений вариантов и соответствующие им частоты, получим вариационный ряд: x 1 x 2 … xk n 1 n 2 … nk, в котором x 1 < x 2 < … < xk. Для сопоставимости вариационных рядов с различными объемами выборок используют значения относительных частот, или частостей, вычисляемых по формуле pi = ni / N. (1.1) Тогда вариационный ряд можно записать в следующем виде: x 1 x 2 … xk p 1 p 2 … pk. Таким образом, вариационным рядом называют перечень вариантов, записанных в возрастающем порядке, с указанием частот или частостей. Для непрерывной случайной величины составляют интервальные вариационные ряды. Для этого весь диапазон значений случайной величины разбивают на ряд интервалов, равных по размеру. Частотой каждого интервала будет являться число значений показателя, попадающих в пределы данного интервала. Среднее значение каждого интервала (середина интервала) является как бы дискретным значением показателя. Вариационный ряд в этом случае записывают в следующем виде:
Здесь (X min¸ X 1) = (X 1¸ X 2) = ××× = (Xk- 1- Xk) = h, где h – величина интервала; h = (x max – x min)/(1 + 3,2 lg N), (1.2) которая дает удовлетворительные результаты при N ³ 200¸300. Если известно среднее квадратическое отклонение показателя s, то величину интервала выбирают из условия, что рассеивание значений показателей внутри интервала несущественно, т.е. h = 0,5s. Следует заметить, что величина h, подсчитанная по формуле (1.2), соответствует приблизительно 0,5s, отсюда можно приблизительно оценить среднее квадратическое отклонение показателя: s @ 2 h. Величина (X max – X min) называется размахом рассеивания значений показателя и является важной статистической характеристикой. Для упрощения вычислений при обработке вариационных рядов удобно пользоваться условными значениями вариантов:
где При резко асимметричном распределении нулевой интервал выбирается независимо от частоты ближе к середине вариационного ряда. Нетрудно убедиться, что при постоянном значении интервала вариационного ряда условные значения вариантов есть целые числа, возрастающие от нуля (интервал со средним значением Для наглядности вариационные ряды могут быть изображены графически в виде полигона, гистограммы, кумулятивной кривой.
Полигон частот или частостей. При построении полигона частот или частостей по оси абсцисс откладывают значения вариантов (для интервального ряда – значения середин интервалов), а по оси ординат – значения частот или частостей (рис.1.1). Полигон, у которого по оси ординат откладывают вероятности вариантов, называют кривой дифференциального распределения. Гистограмма (столбчатая диаграмма). Ее используют при изображении интервальных вариационных рядов. Вариационный ряд изображают в виде прямоугольников (рис.1.2) со сторонами, равными по оси абсцисс – ширине интервала, по оси ординат – частоте или частости интервала.
Кумулятивная кривая. Вариационный ряд может быть записан в виде последовательных сумм частот или частостей. При построении кумулятивной кривой по оси X откладывают значения середин интервалов, а по оси Y – накопленные частоты или частости (рис.1.3). Если используют вероятности, кривая называется кривой интегрального распределения. Приведенные графики вариационных рядов применяют для приближенной оценки характера распределения показателя.
1.3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКИХ ЗНАЧЕНИЙ ПОКАЗАТЕЛЯ Для обобщенной количественной оценки распределения значений изучаемого показателя вариационного ряда используют характеристики, которые определяют положение центра распределения и размах рассеивания отдельных значений относительно центра. Положение центра распределения определяют математическим ожиданием (средним), модой и медианой. Для оценки рассеивания (вариации, изменчивости) отдельных значений относительно центра пользуются дисперсией, средним квадратическим отклонением (стандартом), коэффициентом вариации, асимметрией, эксцессом. В основе вычисления числовых характеристик распределения случайных величин лежит метод моментов. В теории и практике используют начальные, центральные и условные моменты. Начальным моментом порядка k случайной величины X называют математическое ожидание k -й степени этой величины: m k = M (Xk). (1.4) Начальный момент первой степени m1 = M (X) = c является математическим ожиданием случайной величины X, т.е. величиной постоянной. Центральным моментом порядка k случайной величины X называют начальный момент того же порядка центрированной величины X 0 = X – c = X – M (X). Центральные моменты математически выражаются формулой a k = M Центральный момент первого порядка равен нулю: a1 = M (X – c) = = M (X) – c = 0. Центральный момент второго порядка является дисперсией по определению: a2 = M [(X – c)2] = D (X) = s2. Условным моментом порядка k случайной величины X называют начальный момент того же порядка, вычисленный для условных вариантов по формуле (1.3). Математически он представляется в следующем виде:
При обработке вариационных рядов по рабочим формулам вычисляют эмпирические (выборочные) начальные, центральные и условные моменты. Начальный эмпирический момент: · по несгруппированным данным
· по сгруппированным данным
Центральный эмпирический момент: · по несгруппированным данным
· по сгруппированным данным
Условный эмпирический момент: · по несгруппированным данным
· по сгруппированным данным
где ai – условное значение вариантов, определяемое по формуле (1.3). 1.3.1. Характеристики центра распределения Среднее выборочное значение показателя Модой Мо называют значение показателя, которое имеет наибольшую вероятность (частоту или частость). Интервал вариационного ряда, имеющий наибольшую частоту (частость), называют модальным. Значения внутри модального интервала вычисляют, исходя из положения, что изменение частоты в модальном и смежных с ним интервалах происходит по параболе (рис.1.4, а). На этом основании получена формула
где
Медианой Ме называют значение показателя в выборке, которое делит ряд распределения по частоте или частости на две равные части. Медианным интервалом является интервал, в котором находится половина накопленных частот или частостей. В интервальном вариационном ряду медиану определяют, исходя из пропорциональности (рис.1.4, б) значений показателя частоте или частости (изменение по линейному закону). На этом основании получена формула
где Моду и медиану используют для приближенной оценки симметричности распределения. При симметричном распределении
1.3.2. Характеристики рассеивания
Выборочная дисперсия вычисляется по формулам
где Следует отметить, что по приведенным формулам получается смещенная оценка дисперсии. Для получения несмещенного значения применяют формулу Среднее квадратическое отклонение (стандарт) равно корню квадратному из дисперсии Коэффициент вариации n характеризует относительную величину рассеивания значений показателя. Этот коэффициент позволяет сопоставлять размах рассеивания показателей, разнородных как по абсолютной величине, так и по единицам. Коэффициент вариации обычно вычисляют в процентах по формуле
Асимметрия. Рассеивание отдельных значений показателя относительно среднего может быть симметричным и асимметричным. Для симметричных распределений центральные моменты нечетных порядков равны нулю. Несоблюдение этого условия свидетельствует об асимметричности (скошенности) распределения. В этом случае возрастает влияние крайних значений и центральные моменты нечетной степени (при k > 1) не будут равны нулю. Для суждения об этом достаточно получить центральный момент третьего порядка. Для удобства сопоставления разнородных показателей обычно используют безразмерный коэффициент асимметрии, вычисляемый по формуле A = a3 / s3, (1.18) где a3 – центральный момент третьего порядка, определяемый по формуле (1.9) или (1.10) при k = 3. Величину A называют асимметрией распределения случайных величин. Положительный знак величины A (A > 0) указывает на левостороннюю асимметрию, отрицательный (A < 0) – на правостороннюю, равенство нулю (A = 0) – на отсутствие асимметрии (распределение случайных величин симметричное). При обработке даже симметричных эмпирических распределений в силу влияния случайных факторов почти всегда A ¹ 0, поэтому асимметрию считают существенной, если по абсолютному значению она превышает значение 3s А, где s А – среднее квадратическое отклонение величины A, определяемое по формуле
Асимметрию считают несущественной, если A < 3s А. Эксцесс. Для оценки «крутизны» («вершинности») эмпирической кривой распределения по сравнению с кривой нормального распределения используют показатель эксцесса. Из свойств нормального закона распределения следует, что центральные моменты четных порядков подчиняются следующей закономерности [8]:
В частности, при k = 1 будем иметь
откуда При k = 2 по (1.20) получим
Отсюда коэффициент эксцесса
где Невыполнение равенства (1.22) свидетельствует об отклонении вершины фактического распределения от кривой нормального распределения. При Э > 0 вершина эмпирической кривой расположена выше вершины нормальной кривой, а при Э < 0 – ниже. Эксцесс считается существенным, если он по абсолютному значению превышает 3sэ, где sэ – среднее квадратическое отклонение эксцесса, вычисляемое по формуле
1.4. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ Распределение показателя – это совокупность его значений с соответствующими частотами, частостями или вероятностями. Результаты выборок имеют эмпирическое распределение значений показателя, которое при достаточно представительном объеме характеризует распределение показателя в исследуемой генеральной совокупности. Распределение показателя в генеральной совокупности, выражающее в математической форме взаимосвязь значений показателя и их вероятностей, называют законом распределения. Очевидно, что закон распределения есть отражение природы изучаемого явления или процесса. Вследствие разнообразия последних в различных отраслях знания получили распространение различные законы распределения, с которыми для познания природы процесса сравнивают эмпирические распределения. В маркшейдерском деле чаще всего используют следующие основные законы распределения: 1) нормальное; 2) гамма-распределение; 3) распределение Вейбулла; 4) логарифмически нормальное (логнормальное); 5) c2-распределение; 6) F -распределение (распределение Фишера – Снедекора); 7) распределение Стьюдента.
1.4.1. Закон нормального распределения
Если на изучаемый показатель влияет большое число случайных факторов и при этом степень влияния каждого из них невелика и не имеет существенного преимущества по сравнению с другими, то распределение значений такого показателя наиболее близко соответствует закону нормального распределения (рис.1.5).
В маркшейдерском деле указанному условию, как правило, удовлетворяют погрешности маркшейдерских съемок и измерений, размеры отклонений параметров горных выработок от проектных, погрешности химических анализов и различного рода испытаний горных пород в лабораториях, а также распределение показателей свойств горных пород по некоторым месторождениям. Нормальное распределение описывают дифференциальной или интегральной функциями соответственно
Для практических расчетов используют таблицы вероятностей нормального распределения [7]. Поскольку в приведенном виде значение функции зависит от значения и единицы показателя, при составлении таблиц вероятностей нормального распределения используют нормированную функцию, вводя безразмерную переменную (коэффициент вероятности)
После дифференцирования выражения (1.26) dt = (1/s) dx, поэтому dx = s dt, и с учетом (1.26) нормированная функция нормального распределения примет вид
Заметим, что в таком виде нормальный закон распределения заложен во всех программных продуктах, связанных с математической статистикой. Приближенная оценка соответствия эмпирического распределения изучаемого показателя закону нормального распределения производится в следующей последовательности: 1) визуальной оценкой симметричности относительно среднего полигона эмпирических частот или частостей; 2) оценкой равенства среднего, моды и медианы; 3) оценкой равенства нулю значений асимметрии и эксцесса; 4) оценкой коэффициента вариации, который для нормального распределения, как правило, не превышает 50 %. Рассмотрим распределение угловых невязок в 100 треугольниках аналитической сети карьера (табл.1.1, графы 1,2). Предполагая, что по своей природе распределение невязок должно соответствовать закону нормального распределения, вычислим вероятности значений невязок, используя формулу (1.27).
Таблица 1.1 Таблица 1.2
Параметры b, m распределения Вейбулла [5]
1.4.4. Логарифмически-нормальное распределение Поскольку наиболее изученным является закон нормального распределения, ряд асимметричных распределений можно преобразовать в симметричные, если рассматривать распределение логарифмов значений исследуемого показателя. Этот способ преобразования применяют для резко асимметричных распределений с показателем асимметрии до + 7 и коэффициентом вариации до 130 %. Распределения логарифмов значений показателя, подчиняющиеся закону нормального распределения, называют логарифмически-нормальными (логнормальными). Рассмотрим порядок вычисления вероятностей логнормального распределения. 1. Показатели x 1, x 2, …, xn пересчитываются в логарифмы: lg x 1, lg x 2, …, lg xn (можно в натуральные логарифмы, т.е. в ln xi). 2. По формуле (1.2) определяется интервал вариационного ряда:
3. Составляется вариационный ряд из логарифмов рассматриваемого показателя. 4. Используя обычную методику, вычисляют: · среднее значение логарифма
· среднее квадратическое отклонение логарифма
· нормированные границы интервалов
5. По вычисленным значениям ti, используя таблицы нормального распределения, определяют накопленные вероятности значений до верхних границ интервалов F (ti) и вероятности значений интервалов f (ti) по формуле (1.28). Остальные законы распределения будут рассмотрены применительно к проверке статистических гипотез и дисперсионному и фрактальному анализам.
2. ОСНОВЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА 2.1. ОБЩИЕ ПОНЯТИЯ. ФУНКЦИОНАЛЬНЫЕ И СТАТИСТИЧЕСКИЕ ЗАВИСИМОСТИ При изучении различных горно-геологических процессов, выполнении измерений часто необходимо установить, влияет ли один из изучаемых показателей на другой, и если да, то можно ли это влияние выразить в математической форме, в виде уравнения их взаимосвязи, и в дальнейшем этот локальный закон использовать в качестве прогнозной характеристики изучаемых процессов. Например, имеем ряды значений показателей xi и yi: x 1, x 2, x 3 y 1, y 2 y 3.
Как видно из рис.2.1, два эти показателя взаимозависимы. У данной зависимости каждому значению xi соответствует только одно конкретное значение yi. Такого рода зависимости называют функциональными. Их можно назвать и теоретическими, поскольку в опыте, производя определения показателей, которые заведомо связаны функциональной зависимостью, из-за погрешностей измерений можно при одном и том же значении аргумента xi получить несколько значений yi. Например, в уравнении вида S = p d 2/4 определенному значению d теоретически соответствует только одно значение S. Вычертим несколько окружностей одинакового диаметра и измерим их площадь известными в маркшейдерии методами – палеткой или планиметром. В результате получим несколько значений площади. Причина многозначности – погрешности измерений. В маркшейдерском деле часто изучают взаимосвязь таких показателей, на значения которых оказывают влияние не только погрешности измерений, но и целый ряд других факторов, обычно их не учитывают. Тогда для одного и того же значения x в результате измерений получим несколько значений y: при x 1 Þ y 1, y 2, y 3, при x 2 Þ y 4, y 5, y 6. Для установления зависимости yi от xi вычислим средние Числа Уравнения, выражающие зависимость условных средних одного показателя от другого (аргумента), называют уравнениями регрессии yi на xi или корреляционными уравнениями. В данном случае связь двух показателей yi и xi проявляется в изменении статистической характеристики показателя Когда с изменением показателя x частное среднее На практике чаще всего изучают сложные взаимосвязи показателей, когда на y помимо x оказывает влияние целый ряд других показателей. В этом случае метод корреляционного анализа дает возможность в определенной степени исключить эти побочные влияния и получить зависимость для случая, когда эти побочные факторы как бы не действуют. В действительности эти факторы существуют, поэтому полученная методом корреляции зависимость носит вероятностный характер и дает усредненную оценку значений показателя y в зависимости от x. При этом чем больше мы учтем показателей (аргументов), оказывающих влияние на y, тем с большим приближением к действительности получим связи рассматриваемых показателей. С этой точки зрения корреляционные связи могут быть простые, или парные, типа y = f (x), и сложные, или множественные, типа y = f (x, z, u, …), где x, z, u – показатели (аргументы), влияющие на величину y. По форме корреляционные связи делят на линейные (прямолинейные) и нелинейные. Метод корреляционного анализа включает решение следующих последовательных задач: а) оценку наличия и тесноты связи между показателями; б) установление формы и численного выражения уравнения корреляции. При установлении корреляционных связей, как правило, предварительно исходят из объективных предпосылок возможности причинной связи между изучаемыми явлениями.
2.2. ПОНЯТИЕ О КОЭФФИЦИЕНТЕ КОРРЕЛЯЦИИ
Чем больше неучитываемых факторов будет действовать на показатели x и y и чем сильнее влияние этих факторов, тем, очевидно, теснее будет парная связь между показателями x и y. Это значит, что при одном и том же значении xi рассеивание отдельных значений yi будет большим. Таким образом, степень рассеивания отдельных значений функции y при определенных значениях аргумента x является мерой тесноты связи показателей. Характеристикой рассеивания являются, как известно, отклонения отдельных значений показателя от среднего. Следовательно, значения такого отклонения могут быть использованы для оценки тесноты связи. Поэтому в математической статистике в качестве критерия нали
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.45.82 (0.013 с.) |





 = (X 1 + X min)/2,
= (X 1 + X min)/2,  = (X 2 + X 1) /2,
= (X 2 + X 1) /2,  = (Xk + Xk- 1)/2. Величина интервала может быть подсчитана по формуле Стерджеса
= (Xk + Xk- 1)/2. Величина интервала может быть подсчитана по формуле Стерджеса , (1.3)
, (1.3) – среднее значение показателя в i -м интервале (значение середины интервала);
– среднее значение показателя в i -м интервале (значение середины интервала);  – среднее значение интервала с наибольшей частотой (нулевого интервала).
– среднее значение интервала с наибольшей частотой (нулевого интервала). ) на единицу (в сторону уменьшения показателя – отрицательные, в сторону увеличения – положительные). Абсолютная величина
) на единицу (в сторону уменьшения показателя – отрицательные, в сторону увеличения – положительные). Абсолютная величина  всегда получается кратной h.
всегда получается кратной h.

 = M [(X – c) k ]. (1.5)
= M [(X – c) k ]. (1.5)
 = M (ak) =
= M (ak) =  M [(X – X 0) k ]. (1.6)
M [(X – X 0) k ]. (1.6)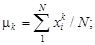 (1.7)
(1.7) . (1.8)
. (1.8) (1.9)
(1.9)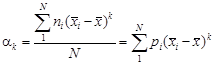 . (1.10)
. (1.10)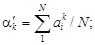 (1.11)
(1.11)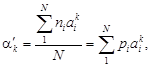 (1.12)
(1.12) (начальный момент первого порядка) определяется согласно приведенным формулам (1.7), (1.8) при k = 1. Среднее выборочное значение показателя
(начальный момент первого порядка) определяется согласно приведенным формулам (1.7), (1.8) при k = 1. Среднее выборочное значение показателя  (1.13)
(1.13) – частости (частоты) предыдущего, модального и последующего интервалов вариационного ряда;
– частости (частоты) предыдущего, модального и последующего интервалов вариационного ряда;  – нижняя граница модального интервала.
– нижняя граница модального интервала.
 (1.14)
(1.14) – нижняя граница медианного интервала;
– нижняя граница медианного интервала;  – накопленная частота или частость до начала медианного интервала;
– накопленная частота или частость до начала медианного интервала;  – частота или частость медианного интервала.
– частота или частость медианного интервала.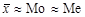 . При левосторонней асимметрии
. При левосторонней асимметрии  ; (1.15)
; (1.15) , (1.16)
, (1.16) – средний квадрат показателя в выборке (начальный момент второго порядка), вычисляемый по формулам (1.7), (1.8);
– средний квадрат показателя в выборке (начальный момент второго порядка), вычисляемый по формулам (1.7), (1.8);  ,
, 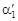 – условные моменты соответственно второго и первого порядка, определяемые по формуле (1.11), (1.12).
– условные моменты соответственно второго и первого порядка, определяемые по формуле (1.11), (1.12). известную из теории погрешности, либо умножают дисперсию, вычисленную по формулам (1.9), (1.10), (1.15), (1.16) на число N / (N – 1). Это целесообразно делать при малых выборках, когда N < 30.
известную из теории погрешности, либо умножают дисперсию, вычисленную по формулам (1.9), (1.10), (1.15), (1.16) на число N / (N – 1). Это целесообразно делать при малых выборках, когда N < 30. и выражается в тех же единицах, что и изучаемый показатель.
и выражается в тех же единицах, что и изучаемый показатель. . (1.17)
. (1.17) . (1.19)
. (1.19) . (1.20)
. (1.20)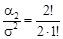 ,
, , что мы имели раньше из (1.5).
, что мы имели раньше из (1.5). . (1.21)
. (1.21)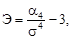 (1.22)
(1.22) – центральный момент четвертого порядка, определяемый по формуле (1.9) или (1.10) при k = 4; для нормального распределения Э = 0.
– центральный момент четвертого порядка, определяемый по формуле (1.9) или (1.10) при k = 4; для нормального распределения Э = 0. . (1.23)
. (1.23)
 (1.24)
(1.24) . (1.25)
. (1.25) . (1.26)
. (1.26) . (1.27)
. (1.27)


 .
.

 для каждого варианта xi:
для каждого варианта xi:  ;
;  .
. .
. остается неизменным, связь между показателями отсутствует.
остается неизменным, связь между показателями отсутствует.


