
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №5. Сведение многокритериальной задачи к однокритериальнойСодержание книги
Поиск на нашем сайте
Цель работы: освоить способ определения наилучшей альтернативы «Сведение многокритериальной задачи к однокритериальной». 5.1 Теоретические сведения Будем представлять принятие решения как действие над множеством альтернатив, в результате которого получается подмножество выбранных альтернатив. Сужение множества альтернатив возможно, если имеется способ сравнения альтернатив и определение наиболее предпочтительных. Каждый такой способ называют «критерием предпочтения». Обратим внимание на то, что при таком описании выбора считают сами собой разумеющимися, уже пройденными, два чрезвычайно важных этапа системного анализа: 1) порождение множества альтернатив, на котором предстоит осуществлять выбор; 2) определение целей, ради достижения которых производится выбор. Будем считать, что исходное множество альтернатив уже задано и преследуемые нами цели определены настолько детально, что уже имеются критерии оценки и сравнения любых альтернатив. Самым простым и наиболее развитым (и, быть может, поэтому чаще употребляемым) является критериальный язык выбора. Такое название языка связано с основным предположением, состоящим в том, что каждую отдельно взятую альтернативу можно оценить конкретным числом (значением критерия), и сравнение альтернатив сводится к сравнению соответствующих им чисел. Пусть
Задача отыскания Чаще всего на практике оценивание любого варианта единственным числом оказывается неприемлемым упрощением. Более полное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по нескольким критериям, качественно различающимся между собой. Например, при выборе конструкции самолета проектировщикам следует учитывать множество критериев: технических, технологических, экономических, социальных, эргономических и пр. Даже в обычной жизни при выборе мы почти никогда не используем единственный критерий: вспомним хотя бы затруднения при выборе подарка ко дню рождения или при выборе места стоянки в турпоходе. Для упрощения процесса поиска наилучшей альтернативы рассмотрим способ «Сведение многокритериальной задачи к однокритериальной». Итак, пусть для оценивания альтернатив используется несколько критериев
Суперкритерий позволяет упорядочить альтернативы по величине
Коэффициенты (частные критерии могут иметь разную размерность) и, во-вторых, в необходимых случаях (как в формуле 4) выполнения условия Итак, при данном способе задача сводится к максимизации суперкритерия:
5.2 Примеры выполнения работы С помощью способа «Сведение многокритериальной задачи к однокритериальной» определим суперкритерий для поиска наилучшей альтернативы системы «мотоцикл». Определим и перечислим основные критерии оценки системы «мотоцикл» и их единицы измерения: стоимость (у. е.), максимальная скорость (км/ч), разгон до 100 км (с), пробег (км), вес мотоцикла (кг), мощность двигателя (л. с.), расход топлива на 100 км (л). Суперкритерий представим в виде аддитивной функции:
Основные значения коэффициентов
Таблица 5.1 - Основные критерии и значения коэффициентов
Для определения суперкритерий нахождения наилучшей альтернативы системы «мотоцикл», используя формулу (5.3), получим следующую зависимость: q0(х) = - q1(х) / 1000 у.е. + q2(х) / 30 км /ч - q3(х)/с - q4 (х) / 100000 км + q5 (х)/30 кг + q6 (х)/ 20 л. с. - q7 (х)/ 1,5 л 5.3 Порядок выполнения лабораторной работы 1. Изучите теоретическую часть данной лабораторной работы. 2. Определите существенные критерии для оценки заданных альтернатив. 3. Определите величину и размерность коэффициентов. 4. Выберите необходимую функцию для определения суперкритерия. 5. Представьте суперкритерий в виде математической зависимости. Варианты систем для выполнения лабораторной работы: 1) процессор; 2) материнская плата; 3) ПЭВМ; 4) звуковая карта; 5) видеокарта; 6) монитор; 7) телефон; 8) автомобильная сигнализация; 9) автомат по сортировке овощей; 10) сканер. 5.4 Содержание отчета Отчет должен включать: 1) цель работы; 2) исходные данные; 3) задачи работы; 4) теоретические сведения; 5) ход выполнения работы; 6) выводы. 5.5 Контрольные вопросы 1. Дайте определение понятия «выбор». 2. Назовите основные требования для определения коэффициентов. 3.Назовите достоинство и недостатки способа «Сведение многокритериальной задачи к однокритериальной».
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.186.233 (0.006 с.) |

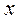 – некоторая альтернатива из множества
– некоторая альтернатива из множества  . Считается, что для всех
. Считается, что для всех 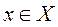 может быть задана функция
может быть задана функция 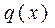 , которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности) и обладает тем свойством, что если альтернатива
, которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности) и обладает тем свойством, что если альтернатива 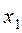 предпочтительнее
предпочтительнее 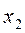 (будем обозначать это
(будем обозначать это 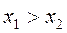 ), то
), то 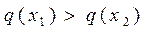 и обратно. Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий
и обратно. Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий 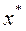 является, естественно, та, которая обладает наибольшим значением критерия:
является, естественно, та, которая обладает наибольшим значением критерия: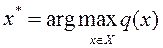 , (5.1)
, (5.1) . Как же тогда осуществлять выбор? Вышеуказанный способ состоит в том, чтобы многокритериальную задачу свести к однокритериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:
. Как же тогда осуществлять выбор? Вышеуказанный способ состоит в том, чтобы многокритериальную задачу свести к однокритериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента: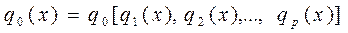 , (5.2)
, (5.2)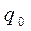 , выделив тем самым наилучшую (в смысле этого критерия). Вид функции
, выделив тем самым наилучшую (в смысле этого критерия). Вид функции 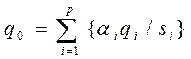 , (5.3)
, (5.3)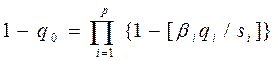 , (5.4)
, (5.4)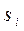 обеспечивают, во-первых, безразмерность числа
обеспечивают, во-первых, безразмерность числа 
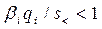 . Коэффициенты
. Коэффициенты 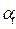 и
и 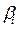 отражают относительный вклад частных критериев в суперкритерий.
отражают относительный вклад частных критериев в суперкритерий.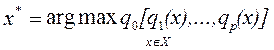 , (5.5)
, (5.5)


