
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий согласия Пирсона о виде распределенияСодержание книги
Поиск на нашем сайте
До сих пор мы предполагали, что закон распределения генеральной совокупности известен. Если закон распределения неизвестен, но есть основания предполагать, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А. Проверка этой гипотезы производится при помощи специально подобранной случайной величины – критерия согласия. Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия, наиболее часто используемым является критерий согласия К.Пирсона («хи квадрат»). Ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности. Пусть по выборке объема n получено эмпирическое распределение: Варианты…………………… Эмпирические частоты……. Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты В качестве критерия проверки нулевой гипотезы примем случайную величину:
Естественно, чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он характеризует близость эмпирического и теоретического распределений. Доказано, что при n®¥ закон распределения случайной величины (А) стремится к закону распределения Число степеней свободы определяется из равенства Построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости
Таким образом, правосторонняя критическая область определяется неравенством Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу H0: генеральная совокупность распределена нормально, необходимо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия Отметим два обстоятельства. Объем выборки должен быть достаточно велик Поскольку возможны ошибки первого и второго рода, следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, построить предварительно график распределения и т.п. Пример. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
Рассчитаем Элементы теории корреляции Две (или несколько) случайных величин могут быть связаны либо функциональной, либо статистической зависимостью. Строгая функциональная зависимость реализуется редко, так как случайные величины подвержены действию случайных факторов, причем среди них могут быть и общие для двух или нескольких величин. В этом случае возникает статистическая зависимость. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой – в этом случае статистическая зависимость называется корреляционной. Пример корреляционной зависимости: урожай зерна Y зависит от количества внесенных удобрений X. С одинаковых по площади участков при равных количествах внесенных удобрений снимают разные урожаи. Это связано с влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, средний урожай зависит от количества удобрений, т.е. Y связано с X корреляционной зависимостью. При рассмотрении взаимосвязей, как правило, рассматривают одну из величин как независимую (объясняющую), а другую как зависимую (объясняющую). При этом изменение первой из них может служить причиной изменения другой. Например, рост дохода ведет к увеличению потребления; рост цены – к снижению спроса; снижение процентной ставки увеличивает инвестиции и т.д. Подобная зависимость не является однозначной в том смысле, что каждому конкретному значению объясняющей переменой может соответствовать не одно, а множество значений из некоторой области. Другими словами, каждому конкретному значению X соответствует некоторое вероятностное распределение зависимой переменной. Поэтому анализируют, как объясняющая переменная (или переменные) влияет (или влияют) на зависимую переменную «в среднем». Зависимость такого типа, выражаемая соотношением:
называется функцией регрессии Y на X. При рассмотрении зависимости двух случайных величин говорят о парной регрессии. Зависимость нескольких переменных, выражаемую функцией Под регрессией понимается функциональная зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой переменной Y, которая строится с целью предсказания (прогнозирования) среднего значения Y при фиксированных значениях независимых переменных. Так как реальные значения зависимой переменной не всегда совпадают с ее средним значением и могут быть различными при данном X (или
называются регрессионными моделями (или уравнениями). Решение задачи построения качественного уравнения регрессии, соответствующего эмпирическим данным и целям исследования, является достаточно сложным и многоступенчатым процессом. Его можно разбить на три этапа: · выбор формулы уравнения регрессии; · определение параметров выбранного уравнения; · анализ качества уравнения и проверка адекватности уравнения эмпирическим данным и, при необходимости, совершенствование уравнения.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.42 (0.008 с.) |

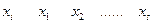
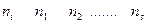
 . При уровне значимости
. При уровне значимости  требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.
требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. (А)
(А)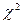 с
с 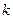 степенями свободы независимо от того, какому закону распределения подчинена генеральная совокупность. Поэтому сам критерий называют критерием согласия
степенями свободы независимо от того, какому закону распределения подчинена генеральная совокупность. Поэтому сам критерий называют критерием согласия  , где s – число групп (частичных интервалов) выборки,
, где s – число групп (частичных интервалов) выборки,  .
. .
. , а область принятия нулевой гипотезы – соответственно неравенством
, а область принятия нулевой гипотезы – соответственно неравенством 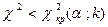 . Обозначим значение критерия, вычисленного по данным наблюдений, через
. Обозначим значение критерия, вычисленного по данным наблюдений, через  и сформулируем правило проверки нулевой гипотезы:
и сформулируем правило проверки нулевой гипотезы: и по таблице критических точек распределения
и по таблице критических точек распределения  . Если
. Если  – нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают, считая, что генеральная совокупность не распределена по нормальному закону.
– нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают, считая, что генеральная совокупность не распределена по нормальному закону. =7,19, число степеней свободы определим по соотношению k= –3=5 (в нашем случае s=8). Используя рассчитанные значения
=7,19, число степеней свободы определим по соотношению k= –3=5 (в нашем случае s=8). Используя рассчитанные значения  находим
находим  . Так как
. Так как  , то нет оснований отвергать нулевую гипотезу. Данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
, то нет оснований отвергать нулевую гипотезу. Данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
 , называют множественной регрессией.
, называют множественной регрессией. ), зависимость должна быть дополнена некоторым слагаемым e, которое, по существу, является случайной величиной. Получающиеся в результате соотношения:
), зависимость должна быть дополнена некоторым слагаемым e, которое, по существу, является случайной величиной. Получающиеся в результате соотношения: или
или



