
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочные уравнения регрессииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для определения значений теоретических коэффициентов, входящих в уравнения регрессии, вообще говоря, необходимо знать и использовать все значения переменных генеральной совокупности, что практически невозможно. В связи с этим по выборке ограниченного объема строится так называемое выборочное (эмпирическое) уравнение регрессии. В силу несовпадения статистической базы для генеральной совокупности и выборки оценки коэффициентов, входящих в уравнение регрессии, практически всегда отличаются от истинных (теоретических) значений, что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к отличающимся друг от друга оценкам. Задача состоит в том, чтобы по конкретной выборке Линейная регрессия Если функция регрессии линейна, то говорят о линейной регрессии. Линейная регрессия (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Для этого простейшего случая имеем:
Последнее соотношение называется теоретической линейной регрессионной моделью; коэффициенты По выборке ограниченного объема строится выборочное уравнение регрессии:
где где отклонение Построенная прямая выборочной регрессии должна наилучшим образом описывать эмпирические данные, т.е. коэффициенты Если по выборке
Необходимым условием существования минимума данной функции двух переменных является равенство нулю ее частных производных по неизвестным параметрам
Отсюда:
выразив из последних соотношений коэффициенты, получим окончательно:
где введены обозначения:
Нелинейная регрессия Многие экономические зависимости не являются линейными, и поэтому их моделирование линейными уравнениями регрессии не может дать положительного реультата. Например, при анализе эластичности спроса по цене применяется так называемая логарифмическая модель, при анализе издержек от объема выпуска – полиномиальная (кубическая) модель. Достаточно широко применяются и многие другие модели – в частности, обратная и экспоненциальная модели. Кратко рассмотрим некоторые из моделей нелинейной регрессии. Логарифмическая модель Пусть некоторая экономическая зависимость моделируется формулой
По МНК можно рассчитать значения параметров аналогично случаю линейной модели (при этом вместо наблюдений Обратная модель Обратная модель имеет вид Степенная модель Степенная функция вида Показательная модель Показательная функция
Прологарифмировав, получаем соотношение:
которое сводится к линейному виду с помощью замен
|
||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1064; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.235 (0.01 с.) |

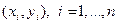 найти оценки неизвестных параметров так, чтобы построенная линия регрессии являлась бы наилучшей, среди всех других линий.
найти оценки неизвестных параметров так, чтобы построенная линия регрессии являлась бы наилучшей, среди всех других линий.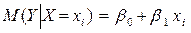 или
или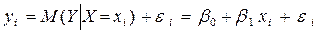
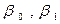 – теоретическими параметрами регрессии;
– теоретическими параметрами регрессии; 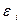 – случайным отклонением.
– случайным отклонением.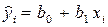 , (1)
, (1)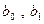 – оценки неизвестных параметров
– оценки неизвестных параметров 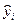 – оценка условного математического ожидания
– оценка условного математического ожидания 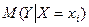 . Для величин
. Для величин 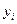 справедлива формула:
справедлива формула:  , (2)
, (2)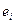 – оценка теоретического отклонения
– оценка теоретического отклонения 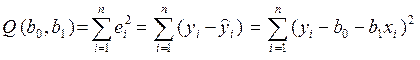 .
.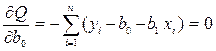
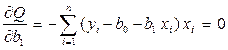 .
.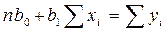
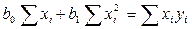 ,
,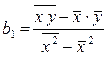
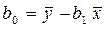 , (3)
, (3) .
.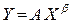 , где A, b – параметры модели. Эта функция может отражать зависимость спроса Y на благо от его цены X
, где A, b – параметры модели. Эта функция может отражать зависимость спроса Y на благо от его цены X  , замена переменных вида
, замена переменных вида 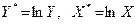 позволяет формально свести уравнение к линейному виду:
позволяет формально свести уравнение к линейному виду: .
.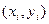 рассматриваются наблюдения
рассматриваются наблюдения 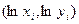 ).
).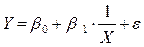 . Заменой
. Заменой 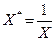 эта модель сводится к линейной. Модель применяется, например, для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции. Кроме этого, классическим примером применения модели является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y.
эта модель сводится к линейной. Модель применяется, например, для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции. Кроме этого, классическим примером применения модели является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y. при m=3 (кубическая функция) в микроэкономике моделирует зависимость общих издержек от объема выпуска; квадратичная функция (m=2) отражает зависимость между объемом выпуска и средними или предельными издержками (или между расходами на рекламу и прибылью). Модель может быть сведена к линейной модели множественной регрессии с помощью замены
при m=3 (кубическая функция) в микроэкономике моделирует зависимость общих издержек от объема выпуска; квадратичная функция (m=2) отражает зависимость между объемом выпуска и средними или предельными издержками (или между расходами на рекламу и прибылью). Модель может быть сведена к линейной модели множественной регрессии с помощью замены 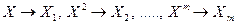 . Параметры модели ищут с помощью МНК.
. Параметры модели ищут с помощью МНК. может использоваться при анализе изменения переменной Y с постоянным темпом прироста во времени. Например, производственная функция Кобба – Дугласа с учетом научно – технического прогресса:
может использоваться при анализе изменения переменной Y с постоянным темпом прироста во времени. Например, производственная функция Кобба – Дугласа с учетом научно – технического прогресса: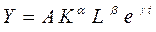 .
.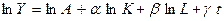 ,
,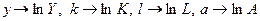 .
.


