
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы переноса выборочных данных на генеральную совокупностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
· метод взвешивания; · метод перевзвешивания; · метод заполнения случайным подбором в классах замещения.
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборке. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности. Выборочные средние и относительные величины распространяются на генеральную совокупность обязательно с учетом предела их возможной ошибки. Приводится выборочный показатель со справкой о пределах ошибки с указанием доверительной вероятности: x̅ ± ∆ x, p ± ∆p. Или же указывают границы значений генеральной характеристики с определенной вероятностью F(t):
Последняя форма записи является основной. Иногда требуется указать только один (верхний или нижний) предел характеристики генеральной совокупности. При испытании качества продукции часто нас не интересуют положительные ошибки выборки (качество фактически выше, чем получилось по выборке), беспокоит нижний предел. В некоторых случаях, напротив, интерес вызывают верхние границы оцениваемых показателей, например при анализе расхода материалов. Так что при характеристике генеральной совокупности всегда указывают неблагоприятный предел. На основе выборки могут быть получены и значения объемных показателей, т. е. подсчетов для генеральной совокупности. Такой расчет осуществляется двумя способами: путем прямого расчета и способом коэффициентов. Прямой расчет заключается в том, что выборочная средняя или доля умножается на объем генеральной совокупности:
Так как средняя величина имеет ошибку репрезентативности ± ∆, то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах
Итоговый подсчет по генеральной совокупности можно получить на основе итогового подсчета по выборке, разделив его на долю отбора единиц совокупности
Прежде чем проводить расчет объемных показателей для генеральной совокупности, нужно убедиться, что структура выборки соответствует структуре генеральной совокупности. При наличии значительных смещений в структуре выборки в долях отдельных групп (0,03 и выше) следует применить метод перевзвешивания, т. в. рассчитывать генеральную среднюю на основе выборочных средних по группам и удельного веса этих групп в генеральной совокупности:
где wi = NiN.
При способе коэффициентов также используются не только выборочные данные, но и сведения о генеральной совокупности. Этот способ основан на связи признаков друг с другом. Например, в результате выборочного обследования семей города получены размер среднедушевого дохода (х̅), средний доход семьи (у̅) и среднее число человек в семье (z̅). Так что x̅ = y̅ / z̅. Зная численность населения города, требуется рассчитать общую величину денежного дохода населения. Очевидно, это можно сделать, умножив душевой доход на общее число жителей в городе: x̅N. Общий доход можно получить, суммируя доход отдельных семей; численность населения можно получить, суммируя данные о числе членов семей. Тогда
Средний душевой расход
Следовательно,
31) Изучение взаимосвязи социально-экономических явлений как важнейшая задача статистической науки.
Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения - это такая связь явлений и процессов, когда изменение одного из них - причины ведет к изменению другого - следствия.
Финансово-экономические процессы представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих процессов необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.
В основе первого этапа статистического изучения связи лежит качественный анализ, связанный с анализом природы социального или экономического явления методами экономической теории, социологии, конкретной экономики. Второй этап - построение модели связи, базируется на методах статистики: группировках, средних величинах, и так далее. Третий, последний этап - интерпретация результатов, вновь связан с качественными особенностями изучаемого явления. Статистика разработала множество методов изучения связей. Выбор метода изучения связи зависит от познавательной цели и задач исследования.
Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называются результативными.
В статистике различают функциональную и стохастическую зависимости. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.
32) Основные задачи корреляционно-регрессионного анализа и практика их реализации. Основные задачи корреляционно-регрессионного анализа · Выявления наличия (или отсутствия) корреляционной связи между изучаемыми признаками. · Определение формы корреляционной зависимости, то есть вида функции регрессии (линейной, логарифмической, параболической и др.). · Построение уравнения регрессии. · Оценка степени тесноты корреляционной связи.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 765; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.35.116 (0.007 с.) |

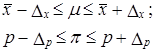
 .
.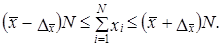
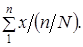
 ,
, .
. представляет собой коэффициент, подсчитанный по выборке, который связывает две характеристики. Этот коэффициент рассчитывается как отношение двух итоговых подсчетов по выборке:
представляет собой коэффициент, подсчитанный по выборке, который связывает две характеристики. Этот коэффициент рассчитывается как отношение двух итоговых подсчетов по выборке: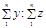 .
.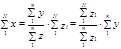 .
.


