
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление ошибок выборочного наблюдения для собственно-случайного и механического отбора.Содержание книги
Поиск на нашем сайте
Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (например, средней) получить достоверные суждения об аналогичных показателях (средней) в генеральной совокупности. При этом следует иметь в виду, что при статистических исследованиях возникают ошибки двух видов: регистрациии репрезентативности.
Ошибки выборки Рассмотрим подробно перечисленные выше способы формирования выборочной совокупности и возникающие при этом ошибки репрезентативности. Собственно-случайный отбор «в чистом виде» в практике выборочного наблюдения применяется редко, но он является исходным среди других видов отбора, в нем реализуются основные принципы выборочного наблюдения. Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки. Ошибка выборочного наблюдения – это разность между величиной параметра в генеральной совокупности, и его величиной, вычисленной по результатам выборочного наблюдения. Для средней количественного признака ошибка выборки определяется
· объема выборки: чем больше численность, тем меньше величина средней ошибки; · степени изменения изучаемого признака: чем меньше вариация признака, а, следовательно, и дисперсия, тем меньше средняя ошибка выборки. При случайном повторном отборе средняя ошибка рассчитывается При случайной бесповторной выборке приведенные формулы корректируются на величину Начало отсчета выбирается разными способами: случайным образом, из середины интервала, со сменой начала отсчета. Главное при этом – избежать систематической ошибки. Например, при 5% выборке, если первой единицей выбрана 13-я, то следующие 33, 53, 73 и т.д. По точности механический отбор близок к собственно-случайной выборке. Поэтому для определения средней ошибки механической выборки используют формулы собственно-случайного отбора.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.84.128 (0.006 с.) |

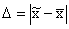
 называется предельной ошибкой выборки.
называется предельной ошибкой выборки. 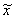 является случайной величиной, которая может принимать различные значения в зависимости от того, какие единицы попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки
является случайной величиной, которая может принимать различные значения в зависимости от того, какие единицы попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки 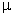 , которая зависит от:
, которая зависит от: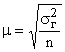 .
. доказано, что
доказано, что 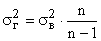 .
.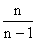 при достаточно больших n близка к 1, можно считать, что
при достаточно больших n близка к 1, можно считать, что 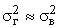 . Тогда средняя ошибка выборки может быть рассчитана:
. Тогда средняя ошибка выборки может быть рассчитана: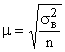 .
.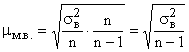 .
.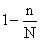 . Тогда средняя ошибка бесповторной выборки:
. Тогда средняя ошибка бесповторной выборки: 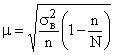 и
и 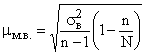 .
.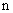 всегда меньше
всегда меньше 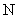 , то множитель (
, то множитель (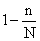 ) всегда меньше 1. Это значит, что средняя ошибка при бесповторном отборе всегда меньше, чем при повторном.
) всегда меньше 1. Это значит, что средняя ошибка при бесповторном отборе всегда меньше, чем при повторном.


