
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Межгрупповая, средняя из внутригрупповых и общая дисперсии. Правило сложения дисперсий.Содержание книги
Поиск на нашем сайте
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних). Общая дисперсия Межгрупповая дисперсия
§ § Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
§ Все три дисперсии (
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации ( Коэффициент детерминации и эмпирическое корреляционное отношение. Дисперсия альтернативного признака. Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Эмпирическое корреляционное среднее варьирует от 0 до 1.
Находят эмпирическое корреляционное отношение обычно в следующих типах задач: Формула дисперсии альтернативного признака Исходя из изложенного выше, можно вывести формулу нахождения дисперсии альтернативного признака, если нам известна процентная доля такого признака в общем объеме выборки.
Таким образом, сумма доли элементов, в которых элементы статистического ряда имеют значение признака "нет" и элементов ряда, которые имеют значение признака "да" - равно единице.
Для нахождения среднего значения ряда, подставим значения альтернативных признаков (0 и 1) в формулу нахождения среднего взвешенного значения статистического ряда. Откуда, совершенно очевидно, в знаменателе будет единица, а в числителе - процентное значение элементов "1". То есть ровно процентное значение элементов с признаком "1". (Формула 2) Формула дисперсии - это средневзвешенное значение квадратов отклонений каждого значения ряда данных. (Формула 3) Поскольку в нашем ряду данные имеют только два типа значений - "0" и "1", то формула нахождения дисперсии для ряда, имеющего альтернативный признак сводится к Формуле 4. Пояснение. поскольку мы только что вывели, что среднее значение выборки равно р (Формула 2), то значение квадрата разности значения (0/1) и среднего значения, согласно Формулы 1, будет в первом случае (1-p)2, а во втором случае (1-q)2, теперь, применив следствие из первой формулы: q = 1 - p, p = 1- q. Получим p2 и q2. Соответственно, доля значений "0" и "1" равна p и q, в результате в числителе и получается q2 p и p2 q. Сумма долей признаков значений "0" и "1" согласно Формуле 1 равна 1. В итоге Формула 4 и принимает значение pq, которое и будет равно значению дисперсии альтернативного признака. Исходя из найденного значения величины дисперсии альтернативного признака, найдем среднеквадратичное отклонение (Формула 5). Поставив значение из Формулы 1 в Формулу 5, получим формулу среднеквадратичного отклонения для дисперсии ряда с альтернативным признаком.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.005 с.) |

 характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий. измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
 — групповые средние,
— групповые средние, — численность единиц i -й группы
— численность единиц i -й группы
 — дисперсия i-ой группы.
— дисперсия i-ой группы. ) связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
) связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
 ) и эмпирическое корреляционное отношение (
) и эмпирическое корреляционное отношение (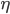 )
) или
или 

 Изначально мы предполагаем, что признак принимает только два значения.
Изначально мы предполагаем, что признак принимает только два значения.


