
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды статистических группировокСодержание книги Поиск на нашем сайте
При проведении группировки приходится решать ряд задач: 2) определение числа групп и величины интервалов; 3) при наличии нескольких группировочных признаков описание того, как они комбинируются между собой; 4) установление показателей, которыми должны характеризоваться группы, т.е. сказуемого группировки. При проведении группировки приходится решать ряд задач: Виды группировок по признакам Содержание статистической информации: Первичная, Вторичная Число группировочных признаков: Простая, Комбинированная, Многомерная Задачи, решаемые с помощью группировки: Типологическая, Структурная, Аналитическая, Территориальная Первичная группировка производится на основе сортировки первичных исходных данных. Вторичная группировка (перегруппировка) - на базе уже имеющихся группировок. Существует два способа образования новых укрупненных групп: 1. изменение интервалов первичной группировки; 2. выделение определенной доли единиц совокупности.
Простая группировка - группировка, выполненная по одному признаку. Многомерная группировка производится по двум и более признакам. К омбинационная группировка базируется на двух и более признаках, взятых во взаимосвязи, в комбинации.
Типологическая группировка - это разделение разнородной совокупности на однокачественные группы {частные совокупности), которые отличаются типом явлений. Структурная группировка предназначена для изучения составных частей совокупности по какому-либо варьирующему признаку. Анализ структурных группировок взятых за ряд периодов или моментов времени, показывает изменения структуры изучаемых явлений, то есть структурные сдвиги. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития. Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками. Территориальная группировка - средство изучения территории изучаемых явлений. Научно обоснованные группировки подчинены задачам исследования. Они исключают формализм при образовании интервалов, дают возможность применять специализированные группировочные признаки и специализированные интервалы.
Группировочный признак - признак, по которому происходит объединение (или разъединение) отдельных единиц совокупности в отдельные группы.
8) Методология группировок. Для построения групп-к необходимо решить 2 задачи: 1)выбрать группировочный признак; 2)определить число групп. Способы проведения: 1)построение дискретного вариац-го ряда, т.е. распределение ед. совок-ти по дискретному признаку, принимающему только целые значения. Напр, есть данные о кол-ном составе 50 семей: 2,3,4,1 и тд. Группируем в табл: число чел-к в семье; кол-во семей; удел вес,%. 2)построение интерв-го вариа-го ряда – оно целесообразно при непрерывной вариации признака, также если число вариантов прерывного признака достаточно велико. Напр, есть данные о величине вкладов в банк 50 физ лиц: 300,1000,3.500,800,и тд. Груп-м данные в табл, разбивая все данные на группы по интервалам. Колонки: группы по сумме вкладов; число вкладчиков; сумма вкладов (всего; в среднем в группе).
9) Статистические таблицы их виды и назначение. Статистическое представление информации возможно в тексте, в таблице, на графике. Статистические таблицы Статистические таблицы в сжатой наглядной и удобной для анализа форме позволяют представить собранные данные. Таблицы - своеобразное выражение особого метода статистики, который позволяет исследователю глубже проникнуть в суть изучаемых процессов, понять их внутреннюю взаимосвязь.
Статистическая таблица - это система строк и столбцов, в которых в определенном порядке изложена статистическая информация об изучаемом явлении. Элементами таблицы являются: · Заголовок содержит указание на характеризуемый признак объекта исследования, время, место наблюдения (иногда единицы измерения признака). · Подлежащее характеризует в таблице объект исследования. · Сказуемое - это система показателей, с помощью которых описывается объект исследования. Статистическое сказуемое может быть выражено посредством абсолютных, относительных, средних и иных величин. · Итоговая строка может находится в начале или в конце подлежащего. · Цифровые данные - количественная характеристики исследуемого объекта.
Виды статистических таблиц По характеру подлежащего таблицы: Простая, Групповая, Комбинационная По характеру сказуемого таблицы: С простой разработкой сказуемого, Со сложной разработкой сказуемого Цель изложения: Описательно-информационная, Аналитическая, Типологическая Основные требования, предъявляемые при составлении и оформлении таблиц 1) название таблицы должно кратко отражать задачи обобщения представленной информации, территориальные границы, период или момент времени, к которому относится изучаемая совокупность, единицы измерения, если они одинаковы для всех данных, содержащихся в таблице; 2) многозначные числа следует округлять в пределах одной графы с одинаковой степенью точности (до 0,1, до 0,01 и т.п.); 3) если единицы измерения в поле таблицы неодинаковы, то в сказуемом (подлежащем) нужно указывать единицы измерения статистических данных; 4) графы желательно нумеровать; 5) следует различать «итого» (итог для определенной части совокупности) и «всего» (итог для совокупности в целом); 6) если в таблице приводят проценты роста, то целесообразно величины от 200% и более заменять отношениями в разах; 7) таблица может сопровождаться примечаниями, в которых указывают источники данных, более подробно раскрывают содержание показателей; 8) в поле таблицы не должно быть пустых клеток. При оформлении таблиц обычно применяют условные обозначения: · «-», когда явление отсутствует; · «х», если оно не имеет осмысленного содержания; · «...», когда отсутствуют данные о размере явления (или делается запись «Нет сведений»); · «0,0», если есть соответствующая информация, но числовое значение меньше принятой в таблице точности. 9) в таблице не должно быть ни одной лишней линии, только необходимые: линия, отделяющая заголовок таблицы от заголовков ееграф, заголовки граф от цифровых данных. Иногда используется линия, отделяющая итоговую строку. Вертикальная разграфка может быть, а может и отсутствовать.
10) Вторичная группировка, методы ее проведения. Группировка - это расчленение изучаемой статистической совокупности на части по одному или нескольким группировочным признакам. Правильно проведенная группировка в значительной мере обеспечивает достоверность всего статистического исследования. Первичная группировка производится на основе сортировки первичных исходных данных.
Группировки, построенные за один и тот же период времени, но для разных регионов или, наоборот, для одного региона, но за два разных периода времени, могут оказаться несопоставимыми из-за различного числа выделенных групп или неодинаковости границ интервалов. В таком случае необходима перегруппировка данных с помощью вторичной группировки. Вторичная группировка - операция по образованию новых групп на основе ранее осуществленной группировки. Применяют два способа образования новых групп. 1. наиболее простой и распространенный способ - изменение (чаще укрупнение) первоначальных интервалов. 2. Долевая перегруппировка - способ состоит в образовании новых групп на основе закрепления за каждой группой определенной доли единиц совокупности.
11) Плотность распределения (абсолютная и относительная). Группировка - это расчленение изучаемой статистической совокупности на части по одному или нескольким группировочным признакам. Правильно проведенная группировка в значительной мере обеспечивает достоверность всего статистического исследования. Вариация - различие значений признака у разных единиц одновременно существующей совокупности. Частоты – f – это численности отдельных вариаций или каждой группы вариационного ряда. Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности. Показатель численности групп представлен либо частотой (абсолютные числа), либо частостью (удельным весом каждой группы - относительные), либо как те и другие совместно (в двух параллельных столбцах). Частость - относительное выражение частоты, представляет собой отношение частоты к сумме частот. Вариационные ряды - ряды распределения, построенные по количественному признаку, определение интервала группировки должно соответствовать переходу от одного качества к другому. Если приходится иметь дело с вариационным рядом с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала. Полученное отношение называется плотностью распределения: Отношения частот или частостей к величинам интервала называются плотностью распределения. Абсолютной плотностью распределения Относительная плотность распределения
Плотность распределения используется как для расчета обобщающих показателей, так и для графического изображения вариационных рядов с неравными интервалами.
12) Относительные величины, их виды, значение и практическое использование. Относительные величины — это отвлеченные статистические величины, выражающие количественное соотношение двух величин. Относительные величины измеряются в коэффициентах, процентах, промилях, комплексных единицах. Виды относительных величин: 1) относительные величины динамики — это отношение фактической величины показателя в отчетном периоде (У1) к фактической его величине в базисном, предшествующем периоде (У0): ОВД = (У1 /У0 )х100%. Относительные величины динамики характеризуют изменение явления во времени. В статистике эти показатели называются темпами роста; 2) относительные величины выполнения плана — это отношение фактической величины показателя (У1) к плановой его величине (Уплан) того же периода: ОВВП = (У1 /Уплан)х 100%. Эта относительная величина показывает степень выполнения плана в процентах; 3) относительная величина выполнения планового задания — это отношение планируемой величины показателя (Уплан) к фактически достигнутой величине в предшествующем периоде, т.е. в базисном (у0): ОВПЗ=(Уплан /У0)х 100%. Показывает, на сколько процентов плановое задание выше (ниже) фактически достигнутого в базисном периоде. Эту величину называют плановым темпом роста; 4) относительная величина структуры — показывает состав явления, выраженный в форме доли или удельного веса. Доля (d) — это отношение части к целому, т.е. отношение составных частей совокупности к ее общему объему. Удельный вес — это доля, выраженная в процентах. Относительные величины структуры используются в статистике для характеристики структурных сдвигов; 5) относительная величина координации — показывает соотношение частей целого, т.о. отношение последовательно всех частей к одной из них, взятой за базу. За базу принимают наименьшее значение. Относительная величина координации показывает, сколько единиц данной части целого приходится на другую ее часть, принятую за базу сравнения; 6) относительная величина интенсивности — это отношение двух разноименных величин, связанных между собой. Характеризует степень развития какого-либо явления в определенной среде; 7) относительная величина сравнения — это отношение одноименных величин, характеризующих разные объекты изучения за один и тот же период. Показывает, во сколько раз числитель больше (меньше) знаменателя.
13) Относительные величины сравнения, выполнения плана. относительные величины выполнения плана — это отношение фактической величины показателя (У1) к плановой его величине (Уплан) того же периода: ОВВП = (У1 /Уплан)х 100%. Эта относительная величина показывает степень выполнения плана в процентах; относительная величина сравнения — это отношение одноименных величин, характеризующих разные объекты изучения за один и тот же период. Показывает, во сколько раз числитель больше (меньше) знаменателя
14) Относительная величина динамики. ) относительные величины динамики — это отношение фактической величины показателя в отчетном периоде (У1) к фактической его величине в базисном, предшествующем периоде (У0): ОВД = (У1 /У0 )х100%. Относительные величины динамики характеризуют изменение явления во времени. В статистике эти показатели называются темпами роста;
15) Относительная величина структуры, наглядности. относительная величина структуры — показывает состав явления, выраженный в форме доли или удельного веса. Доля (d) — это отношение части к целому, т.е. отношение составных частей совокупности к ее общему объему. Удельный вес — это доля, выраженная в процентах. Относительные величины структуры используются в статистике для характеристики структурных сдвигов
16) Методология средних. Применение средних величин. Сущность средней заключается в том, что в ней взаимопогашаются случайные различия и отражается лишь результат влияния основных факторов и выявляется то общее, типичное, что характерно для всех единиц изучаемой совокупности, т.е. характерный уровень признака. Способность средней отражать типичный уровень признака и раскрывать общие закономерности называют законом средних чисел. Этот закон действует при определенных условиях. Остановимся на некоторых общих условиях применения средних величин. 1. При определении средней величины в каждом конкретном случае нужно исходить из качественного содержания осредняемого признака и имеющихся для расчета исходных данных. 2. Средние должны вычисляться на основе массового обобщения факторов. По закону больших чисел при массовом обобщении факторов случайные отклонения индивидуальных величин погашаются в средней величине. Поэтому средняя и выявляет типичный, характерный размер варьирующего признака. 3. Средние должны рассчитываться по качественно однородным совокупностям. Например, рассчитывают среднюю урожайность конкретного вида культур (среднюю урожайность ржи, картофеля, пшеницы и пр.), среднюю заработную плату работников определенной специальности на конкретном предприятии, средний доход студентов в Государственных вузах и т.п. Средние, полученные для неоднородных совокупностей не характеризуют типичного размера признака 17) Относительная величина интенсивности. Абсолютная величина – это показатель, представляющий собой количественную характеристику изучаемых явлений. Относительная величина – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа.
Величина, с которой производится сравнение, называется основанием, или базой сравнения Относительная величина показывает, во сколько раз сравниваемая величина больше или меньше базисной или какую долю первая составляет по отношению ко второй. В ряде случаев относительная величина показывает, сколько единиц одной величины приходится на единицу другой. Результатом сопоставления разноименных величин являются именованные относительные величины. Их название образуется сочетанием сравниваемой и базисной абсолютных величин. Относительная величина интенсивности: Характеризует отношения между разноименными абсолютными величинами, например, отражает степень распространенности изучаемого явления или процесса. ОВИ = Одна совокупность / Другая совокупность (разноименные) Данный показатель получают сопоставлением разноименных, но взаимосвязанных в своем развитии величин. Поэтому наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах, промилле, продецимилле. Обычно относительный показатель интенсивности рассчитывается в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения.
18) Структурные средние, их значение и практическое применение.
Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).
В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.
Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:
19) Расчет моды, медианы и квантилей в интервальном вариационном ряду. Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:
где XMe – нижняя граница медианного интервала; hMe – его величина; (Sum m)/2 – половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении); SMe-1 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; mMe – число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении). При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Для интервального ряда с равными интервалами величина моды определяется как
где ХMo – нижнее значение модального интервала; mMo – число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении); mMo-1 – то же для интервала, предшествующего модальному; mMo+1 – то же для интервала, следующего за модальным; h – величина интервала изменения признака в группах.
Для выражения особенностей формы распределения рассчитываются ранговые характеристики и кривые распределения. Ранговые характеристики носят общее название квантили. Квантили – значения признака, которые делят ряд распределения на равные части Позволяют детально изучить вариационные ряды. Они подразделяются на «семейства»
Квартили - Аналогично медиане вычисляются значения признака, делящие ранжированную совокупность делят на четыре равные части. Ясно, что Q2 совпадает с Me Первый (нижний) квартиль отсекает от совокупности ¼ часть единиц с минимальными значениями, а третий (верхний) отсекает ¼ часть единиц с максимальными значениями. С помощью квартилей мы определяем границы, где находятся 50% единиц, наиболее характерные для этой совокупности. При этом вторая квартиль является медианой. Квинтили- ранжированную совокупность делят на пять равных частей
Сикстили - ранжированную совокупность делят на шесть равных частей. Децили - ранжированную совокупность делят на десять равных частей Пример - децильный коэффициент дифференциации населения. Население делится на 10 частей по уровню дохода. Берут первые 10% и последние 10%. Считают, что средний доход последней группы не должен быть больше, чем в 10 раз среднего дохода первой группы. В России официально это превышение составляет 14-16 раз, неофициально – 20 и более раз Перцентили (процентили) - ранжированную совокупность делят на сто равных частей
20) Показатели вариации, их значение и способы расчета. Абсолютные показатели 1. Размах вариации. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:
2. Среднее линейное отклонение (d) вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю. Формула среднего линейного отклонения (простая) Формула среднего линейного отклонения (взвешенная)
Формулы дисперсии взвешенной и простой: 4. Среднее квадратическое отклонение – это квадратный корень из дисперсии. Среднее квадратическое отклонение простое Среднее квадратическое взвешенное
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.013 с.) |

 называется число, показывающее, сколько единиц совокупности приходится на единицу размера интервала в отдельных группах ряда
называется число, показывающее, сколько единиц совокупности приходится на единицу размера интервала в отдельных группах ряда 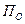 определяется как частное от деления частности W отдельной группы ряда на единицу размера интервала
определяется как частное от деления частности W отдельной группы ряда на единицу размера интервала













 .
. .
.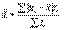 .
. 3. Дисперсия – это среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
3. Дисперсия – это среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения. .
. .
.


