Расчетное значение F-критерия сравнивают с табличным

Если Fp>Ft, то опыт доказывает с вероятностью большей заданной влияние фактора на результативный признак;

Если Fp=Ft, то опыт доказывает с заданной вероятностью влияние фактора на результативный признак;

Если Fp<Ft, влияние фактора на результативный признак не доказано, но не доказано и отсутствие влияния фактора. Опыт необходимо повторить, уравнивая группы по факторам, за исключением изучаемого фактора, или увеличить количество единиц изучаемой совокупности.

Если Fp<<Ft, то рассчитывают F*p

 

Теоретическое значение F-критерия в данном случае определяют при заданном уровне значимости по таблицам на пересечении строки и столбца, соответствующим двум степеням свободы дисперсий: по строке -факторной; по столбцу - остаточной.

Если F*p>F*t, то опыт достоверно доказывает отсутствие влияния фактора на результативный признак.

 

23) Выборочное статистическое наблюдение. Виды выборок. Ошибки репрезентативности.

Выборочное наблюдение — это такой тип несплошного наблюдения, при котором обследованию подвергаются не все единицы изучаемой совокупности, а лишь отобранные в определенном порядке.

Применение выборочного наблюдения способствует:

1) экономии времени и средств в результате сокращения объема работ;

2) минимизации порчи или уничтожения исследуемых объектов;

3) возможности детального исследования каждой единицы наблюдения при неосуществимости охвата всех единиц;

4) достижению большей точности результатов обследования.

Выборочная совокупность (выборка) (n) — это совокупность случайно отобранных объектов из генеральной совокупности.

Генеральная совокупность (N) — это совокупность объектов, явлений или процессов, из которых производится выборка.

Прогностическая функция статистики состоит в оценивании вероятностей тех или иных случайных событий, которые происходят в изучаемом процессе, показателей тех или иных случайных величин, связанных с этим процессом. Эта функция служит основой для принятия управленческих решений. С помощью этой функции можно получить сигнал о возможности появления кризисных явлений в изучаемом процессе, если не внести каких-то изменений в управление им.

 

Аналитическая функция статистики состоит, во-первых, в количественном исследовании тенденций развития процесса; во-вторых, в изучении этого процесса в динамике; в-третьи, в измерении связей между разными факторами, влияющими на процесс, и его результатами.

Ошибки репрезентативности -отклонение значения показателя обследованной совокупности от его величины по исходной совокупности. Ошибки репрезентативности характерны только для несплошного наблюдения. Они возникают потому, что отобранная и обследованная совокупность недостаточно точно воспроизводит (репрезентирует) всю исходную совокупность в целом.

Ошибки репрезентативности

• Случайные
• Средние ошибки
• Предельные ошибки
• Системные

 

 

24) Собственно-случайная, средняя и предельная ошибки выборки. Коэффициент доверия.

Собственно случайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом. Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.

 

Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

В собственнослучайный отборе заключаются и реализуются основные принципы выборочного статистического наблюдения.

 

Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.

Выборочная доля w, или частность, определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности п.

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:

для средней количественного признака: ех = \х – х\;

для доли (альтернативного признака): ew = \х – p\.

Только выборочным наблюдениям присуща ошибка выборки.

Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Средняя ошибка выборки зависит от степени варьирования изучаемого признака.

Механическая выборка – это отбор единиц в выборочную совокупность из генеральной, которая разбита по нейтральному признаку на равные группы; производится так, что из каждой такой группы в выборку отбирается лишь одна единица.

При еханическом отборе единицы изучаемой статистической совокупности предварительно располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал.

Предельная ошибка - максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления. 1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:

где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;

мю х — средняя ошибка выборки.

 

25) Средняя и предельная ошибка выборки в типической выборке.

Типическая выборка. При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.

Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации.

Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.

При типическом и серийном отборе, при расчете ошибки выборки вместо общей дисперсии (σ²) следует использовать среднюю из внутригрупповых дисперсий и межгрупповую дисперсию , где 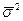- частная дисперсия i группы, объем i группы