
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициенты Фехнера и СпирмэнаСодержание книги Поиск на нашем сайте
При наличии количественных признаков используется коэффициент Фехнера и коэффициент Спирмена. Коэффициент Фехнера - мера тесноты связи - отношение разности числа пар совпадающих и несовпадающих пар знаков к сумме этих чисел:
где С - количество совпадающих знаков отклонений X и У от их средней; Н - количество несовпадающих знаков отклонений от средней (С+Н=n) Коэффициент Фехнера не учитывает величину отклонений признаков от средних значений, но он может служить некоторым ориентиром в оценке интенсивности связи. В данном случае он указывает на тесную связь признаков.
Ранговый коэффициент Спирмэна где
При наличии качественных (атрибутивных) признаков рассчитываются: · коэффициент ассоциации, · коэффициент контингенции, · коэффициент сопряженности К.Пирсона, · коэффициент сопряженности А.Чупрова.
39) Построение параллельных рядов и количественная оценка их взаимосвязи. 40) Показатели тесноты связи качественных признаков. 41) Динамические ряды, основные элементы и правила их построения. Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности. Каждый динамический ряд содержит две составляющие: 1) показатели периодов времени (годы, кварталы, месяцы, дни или даты); 2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда. Уровни ряда выражаются как абсолютными, так и средними или относительными величинами. В зависимости от характера показателей строят динамические ряды абсолютных, относительных и средних величин. Ряды динамики из относительных и средних величин строят на основе производных рядов абсолютных величин. Различают интервальные и моментные ряды динамики. Динамический интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги. Динамический моментный ряд отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются
42) Абсолютные и относительные показатели динамики. Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.
Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле
Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).
Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле
Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».
43) Средние величины в динамических рядах. Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени. Для моментных рядов динамики с равностоящими уровнями средний уровень определяется по формуле средней хронологической моментного ряда:
Для моментных рядов динамики с неравностоящими уровнями средний уровень определяется по формуле средней хронологической взвешенной моментного ряда:
44) Методология выявления тренда в динамических рядах. Проверка на наличие тренда в ряду динамики может быть осуществлена по нескольким критериям.
1) Метод средних. Изучаемый ряд динамики разбивается на несколько интервалов (обычно на два), для каждого из которых определяется средняя величина (). Выдвигается гипотеза о существенном различии средних. Если эта гипотеза принимается, то признается наличие тренда.
2) Фазочастотный критерий знаков первой разности (критерий Валлиса и Мура). Суть его заключается в следующем: наличие тренда в динамическом ряду утверждается в том случае, если этот ряд не содержит либо содержит в приемлемом количестве фазы – изменение знака разности первого порядка (абсолютного цепного прироста).
3) Критерий Кокса и Стюарта. Весь анализируемый ряд динамики разбивают на три равные по числу уровней группы (в том случае, когда число уровней ряда не делится на три, недостающие уровни надо добавить) и сравнивают между собой уровни первой и последней групп.
4) Метод серий. По этому способу каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов: например, если уровень ряда меньше медианного значения, то считается, что он имеет тип А, в противном случае – тип В. Теперь последовательность уровней выступает как последовательность типов. В образовавшейся последовательности типов определяется число серий (серия – любая последовательность элементов одинакового типа, с обоих сторон граничащая с элементами другого типа).
Если в ряду динамики общая тенденция к росту или снижению отсутствует, то количество серий является случайной величиной, распределенной приближенно по нормальному закону (для n > 10). Следовательно, если закономерности в изменениях уровней нет, то случайная величина R оказывается в доверительном интервале
45) Интерполяция и экстраполяция уровней динамического ряда. Выравниванием рядов динамики пользуются для того, чтобы найти значение недостающего члена ряда. Такой способ называется интерполяцией. Экстраполяцией рядов динамики называют прием, который заключается в том, что, продолжая найденные математические кривые можно предсказать дальнейшее развитие событий. Прогнозирование базируется на знании развития прогнозируемого явления, а также факторов, влияющих на это явление и того, каким образом эти факторы могут изменить развитие явления. Приемы изучения сезонных колебаний. Сезонное колебание – это более или менее устойчивые внутригодовые колебания в ряду динамики, обусловленные специфическими условиями производства или потребления данного товара. Сезонные колебания характеризуются индексами сезонности (JS) совокупность которых образует сезонную волну. Индекс сезонности - средняя величина, определенная из % отношений по одноименным месяцам фактических уровней ряда динамики к выровненным уровням. Для выявления сезонных колебаний берут данные за несколько лет с распр6еделением по месяцам, это делается для того, чтобы выявить устойчивую сезонную волну, на которой бы не отражались индивидуальные факторы одного года. Определяя индексы сезонности, пользуются несколькими методами, выбор которых зависит от вида ряда: 1) Если ряд содержит определенную тенденцию в развитии, то прежде чем определить сезонную волну, определяют общую тенденцию, при этом рассчитывают % фактических данных к выровненным, а индекс сезонности по формуле. 2) Если же ряд не содержит ярко выраженную тенденцию, то такой ряд называют стабильным, а индекс сезонности рассчитывают по формуле.
46) Понятие о сезонных колебаниях. Индексы сезонности, их расчет и графическое изображение. Анализ рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития. При относительно неизменном годовом уровне явления индекс сезонности можно рассчитать как процентное отношение средней величины из фактических уровней одноименных месяцев к общему среднему уровню за исследуемый период:
47) Индексный метод в экономико-статистическом анализе. Индексный метод является одним из важнейших методов в статистике. Индексы относятся к числу обобщающих показателей. Следует различать понятие индекса в широком и узком смысле. В широком смысле индекс — это относительная величина, характеризующая изменения явлений во времени (динамику). Но подобные относительные величины могут быть рассчитаны лишь для простых явлений или однородных совокупностей, единицы которых могут быть суммированы. Такие совокупности называются соизмеримыми. Индекс в узком смысле слова — это обобщающий показатель сравнения двух совокупностей, состоящий из элементов, непосредственно не поддающихся суммированию. С помощью индексов решаются две основные задачи: 1) синтетическая задача — обобщение, синтез динамики отдельных элементов в сложные явления в одном обобщающем показателе (сводном индексе); 2) аналитическая задача — анализ влияния изменения отдельных факторов на изменение сложного явления. Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом. ИНДЕКСНЫЙ МЕТОД - метод статистического исследования, позволяющий с помощью индексов соизмерять сложные социально-экономические явления путем приведения анализируемых величин к некоторому общему единству. Метод применяется для изучения динамики явления, позволяет выявлять и измерять влияние факторов на изменение изучаемого явления. (pq)
48) Индексы индивидуальные и сводные. Агрегатные индексы. По степени охвата элементов явления индексы делят на индивидуальные и общие (сводные). Индивидуальные индексы (i) - это индексы, которые характеризуют изменение только одного элемента совокупности. Общий (сводный) индекс (I) характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.01 с.) |

 ,
,
 - разность рангов по обоим признакам для каждого объекта, i = 1,...,n.
- разность рангов по обоим признакам для каждого объекта, i = 1,...,n.

 , где
, где - уровни периода, за который делается расчет;
- уровни периода, за который делается расчет;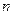 -число уровней;
-число уровней; - длительность периода времени.
- длительность периода времени. , где
, где -уровни рядов динамики;
-уровни рядов динамики; - интервал времени между смежными уровнями.
- интервал времени между смежными уровнями.
 В условиях изменчивости годового уровня индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев:
В условиях изменчивости годового уровня индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев: 



