
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка тесноты связи нелинейной зависимостиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
При наличии нелинейной зависимости (парабола, гипербола, экспонента и т.п.) теснота связи оценивается эмпирическим корреляционным отношением
35) Роль аналитической группировки в изучении взаимосвязи явлений. Группировки, предназначенные для изучения взаимосвязей и зависимостей между явлениями и процессами, называются аналитическими. Многие массовые явления достаточно тесно взаимосвязаны между собой: себестоимость продукции зависит от производительности труда: производительность труда в свою очередь зависит от технического уровня производства и труда, квалификации работников и т.д. Изменение любого экономического явления в конечном счете обуславливается влиянием на него других явлений, с которыми оно связано. При исследовании взаимосвязей принято явления и их признаки подразделять на факторные и результативные. Факторными называются признаки (явления), вызывающие изменение другого, зависящего от них признака (явления). Последний (зависящий) носит название результативного признака (явления). Аналитическая группировка ставит своей целью выявить и установить количественное выражение степени связи между факторным и результативным признаками (явлениями) в конкретных условиях места и времени. Ведь один и тот же фактор в одних условиях может оказывать сильное влияние на результативный признак (явление), в других – слабое. В этом случае говорят о наличии или отсутствии связи между изучаемыми признаками (явлениями). Аналитические группировки строятся по факторному признаку (явлению). Например, изучая взаимосвязь между производительностью труда и себестоимостью продукции предприятия следует сгруппировать по уровню производительности труда.
36) Коэффициент детерминации и его значение. Коэффициент детерминации (R2)— это доля дисперсии отклонений зависимой переменной от её среднего значения, объясняемая рассматриваемой моделью связи (объясняющими переменными). Модель связи обычно задается как явная функция от объясняющих переменных. В частном случае линейной связи R2 является квадратом коэффициента корреляции между зависимой переменной и объясняющими переменными.
Общая формула для вычисления коэффициента детерминации:
где yi — наблюдаемое значение зависимой переменной, а fi — значение зависимой переменной предсказанное по уравнению регрессии
При проверке гипотезы о наличии связи модель связи может быть неизвестна. Тогда ее задают в виде кусочно-постоянной функции (в этом случае коэффициент детерминации равен квадрату корреляционного отношения) либо оценивают неизвестные значения функции связи, используя методы сглаживания эмпирической зависимости Функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50 %. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.
С другой стороны, близость коэффициента детерминации к единице может быть следствием того, что модель излишне точно описывает имеющиеся эмпирические данные, которые содержат случайную составляющую. Например, если у нас имеется n точек, то мы можем подобрать модель в виде полинома n - 1 степени, которая точно пройдет через все точки. Но если эмпирические данные измерены не точно, такая модель не имеет смысла. Поэтому наряду с коэффициентом детерминации используют другие показатели адекватности и качества моделей.
37) Изучение взаимосвязи графическим методом.
38) Ранговый коэффициент корреляции Спирмена, коэффициент корреляции Фехнера.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.01 с.) |


 или
или 
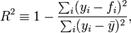
 -среднее арифметическое зависимой переменной.
-среднее арифметическое зависимой переменной.


