
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 7. Изучение взаимосвязи социально-экономических явленийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель: усвоить и закрепить материал по теме, научиться анализировать взаимосвязи социально-экономических явлений с помощью методов статистики. Исследование объективно существующих связей между явлениями – важнейшая задача общей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие существенное влияние на вариацию изучаемых явлений и процессов. Знание характера и силы связи позволяет управлять социально-экономическими явлениями, предсказывать их развитие. Причинно-следственные отношения - это связь явлений и процессов, при которой изменение одного из них - причины - ведет к изменению другого - следствия. Признак, характеризующий следствие, называется результативным; признаки, характеризующие причины, - факторными. Задача изучения взаимосвязей в общем виде состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. На практике наиболее широкое применение нашли приемы корреляционно-регрессионного анализа, которые позволяют количественно выразить взаимосвязь между показателями. Корреляционный анализ подразумевает исследование силы связи. При проведении регрессионного анализа оцениваются форма связи и воздействие одних факторов на другие. Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Наиболее разработанной в теории статистики является методология так называемой парной корреляции ¾ зависимости между двумя случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению другой. Например, зависимость между производительностью труда и объемом производства. Для выявления и оценки связи между изучаемыми признаками в корреляционно-регрессионном анализе необходимо построить регрессионную модель (уравнение регрессии), которая лучше других будет отражать реально существующие связи между анализируемыми признаками. Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой (уравнение однофакторной корреляционной связи): ўx=a + bx, где х — факторный признак; y— результативный признак; а и b — неизвестные параметры уравнения регрессии. Параметры a и b определяются с помощью метода наименьших квадратов из системы нормальных уравнений: ìS yx= na + bSx, í îS yx x= aSx + bSx2, где n— количество наблюдений. Параметр a является свободной переменной и не несет никакого экономического смысла, а параметр b – коэффициент регрессии - при наличии прямой зависимости имеет положительное значение, а в случае обратной зависимости – отрицательное. Кроме того, он показывает, насколько в среднем изменяется величина результативного признака y при изменении факторного признака x на 1. Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака y при изменении факторного признака x на 1%:
Для измерения тесноты связи между факторными и результативными показателями в однофакторном корреляционно-регрессионном анализе определяется коэффициент корреляции, который определяется по следующей формуле:
где х – факторный признак, у - результативный признак,
Коэффициент корреляции принимает значение в интервале от -1 до +1. Если |r|<0,3; то связь слабая; при |r|=(0,3..0,7) – средняя; при |r|>0,7 – сильная (тесная). При |r|=1 связь называется функциональной, а при |r|=0 линейная связь между x и y отсутствует. Квадрат коэффициента корреляции носит название коэффициента детерминации (R2). Величина коэффициента детерминации служит одним из критериев качества линейной модели. Чем ближе его значение к 1, тем меньше роль случайных факторов, и, следовательно, данную линейную модель можно использовать для прогноза значений результативного признака. Типовая задача Известны следующие данные о средней продолжительности жизни и потреблении мяса на душу населения по 20 странам мира:
Определить наличие и форму связи между средней ожидаемой продолжительностью жизни и потреблением мяса на душу населения. Постройте уравнение регрессии и определите его параметры. По приведенным данным вычислите линейный коэффициент корреляции и детерминации, проверьте правильность выбора формы связи. Сделайте выводы. Решение Примем в качестве факторного признака x ¾ потребление мяса на душу населения в год (кг), а в качестве результативного y ¾ среднюю ожидаемую продолжительность жизни (лет). Для выявления наличия связи между признаками построим поле корреляции:
Точки поля корреляции расположены близко друг к другу и группируются вокруг некоторой линии. Таким образом, можно сказать, что связь между признаками х и у присутствует. Предположим, что она линейная, т.е. можно построить такую прямую линию, расстояние от всех точек графика до которой будет наименьшим (см. рис. ниже).
Построим уравнение регрессии и определим его параметры. Уравнением, которое характеризует линейную зависимость между двумя показателями, является уравнение прямой (уравнение однофакторной корреляционной связи): ўx=a + bx, Определим параметры a и b с помощью метода наименьших квадратов, для этого решим систему нормальных уравнений: ìS yx= na + bSx, í îS yx x= aSx + bSx2, где n— количество наблюдений. Построим рабочую таблицу для промежуточных расчетов:
Подставим полученные данные в систему нормальных уравнений: ì1483,8 = 20a + 1464b, í î110044 = 1464a + 116828b. Решив систему уравнений, получим а = 63,21, b = 0,15. Следовательно, уравнение регрессии имеет вид: ўx=63,21 + 0,15x. Таким образом, можно утверждать, что связь между душевым потреблением мяса и ожидаемой продолжительностью жизни прямая (т.к. b > 0), причем при увеличении потребления мяса на 1 кг на душу населения в год, средняя продолжительность жизни увеличивается на 0,15 лет. Для оценки тесноты связи между признаками определим линейный коэффициент корреляции:
Рассчитаем недостающие данные:
Т.к. коэффициент корреляции |r|>0,7, то связь между признаками х и у сильная (тесная). Оценим качество построенной модели (правильность выбора формы связи), для этого определим коэффициент детерминации:
Таким образом, можно утверждать, что на среднюю ожидаемую продолжительность жизни только на 58% влияет факторный признак, т.е. среднедушевое потребление мяса в год. На остальные 42% влияют неучтенные факторы. В данном случае, возможно, целесообразно подобрать другое уравнение регрессии, которое будет более точно описывать связь между изучаемыми признаками. Задачи для самостоятельной работы Задача 7.1 Известны данные по десяти предприятиям за отчетный период:
Для изучения связи между размером среднегодовой стоимости основных производственных фондов и выпуском продукции постройте линейное уравнение регрессии и определите его параметры. По приведенным данным вычислите линейный коэффициент корреляции и детерминации, проверьте правильность выбора формы связи. Задача 7.2 Известны данные по небанковским кредитным организациям:
Для изучения связи между размером собственного и привлеченного капитала постройте линейное уравнение регрессии и определите его неизвестные параметры. По приведенным данным вычислите линейный коэффициент корреляции и детерминации, проверьте правильность выбора формы связи. Задача 7.3 Провести корреляционно-регрессионный анализ душевого дохода под влиянием факторов индекса человеческого развития и индекса человеческой бедности. Исходные данные по странам за 2002 год
Задача 7.4 Для выявления зависимости производительности труда рабочих от стажа их работы был найден линейный коэффициент корреляции, равный 0,8. Кроме того, известны следующие данные: § средний стаж работы на предприятии составляет 5 лет; § среднее квадратическое отклонение по стажу - 2 года; § среднее квадратическое отклонение по производительности труда – 4,4 изделия; § коэффициент вариации по производительности труда 40%. Определите аналитическое уравнение связи, характеризующее зависимость производительности труда от стажа работы. Задача 7.5 По 20 предприятиям была получена модель, отражающая зависимость выпуска продукции в месяц от размера основного капитала: y = 12,0 + 0,5x. Кроме того, известны следующие данные: § средняя стоимость основных фондов на одно предприятие составляет 12 млрд. руб.; § средний размер выпуска продукции на одно предприятие в месяц – 18 млн. руб.; § среднее квадратическое отклонение по стоимости основного капитала – 3,5 млрд. руб.; § среднее квадратическое отклонение по выпуску продукции – 2 млн. руб. Определите степень тесноты связи между размером выпуска продукции и стоимостью основного капитала. Тестовые задания 1. Укажите факторы, связанные наиболее тесно корреляционной зависимостью, если известны значения коэффициентов корреляции: rху =0,35, ryz = 0,78 и rxz = -0,83. A. х и z; B. х и у; C. r и у; D. все факторы не связаны между собой тесной корреляционной связью. 2. Линейный парный коэффициент корреляции изменяется в пределах: A. B. -1<r<+1; C. D. E. - 3. При наличии функциональной линейной зависимости между количественными признаками X и Y коэффициент корреляции rху=.... 4. Обратную связь между признаками показывает коэффициент корреляции... A. rху= 0,982; B. rху= -0,991; C. rху = 0,871. 5. Для измерения тесноты корреляционной связи между двумя количественными признаками используются.... A. коэффициент корреляции знаков; B. коэффициент эластичности; C. линейный коэффициент корреляции; D. коэффициент корреляции рангов. 6. Тесноту связи между двумя качественными альтернативными признаками можно измерить с помощью коэффициентов.... A. знаков Фехнера; B. корреляции рангов Спирмена; C. ассоциации; D. контингенции; E. конкордации. 7. Коэффициент детерминации может принимать значения.... A. от 0 до 1; B. от-1 до 0; C. от -1 до 1; D. любые положительные; E. любые меньше нуля. 8. В результате проведения регрессионного анализа получают функцию, описывающую... показателей. A. взаимосвязь; B. соотношение; C. структуру; D. темпы роста; E. темпы прироста. 9. Прямолинейная связь между факторами исследуется с помощью уравнения регрессии.... A. B. C. D. 10. Параметр a1 (a1= 0,016) линейного уравнения регрессии A. с увеличением признака "х" на 1 признак "у" увеличивается на 0,694; B. с увеличением признака "х" на 1 признак "у" увеличивается на 0,016; C. связь между признаками "х" и "у" прямая; D. связь между признаками "х" и "у" обратная.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1076; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 .
.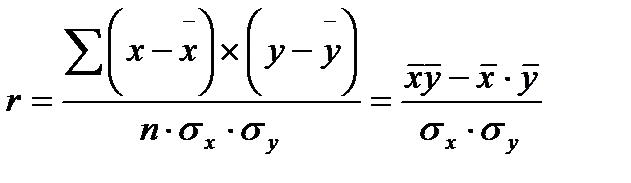 ,
, – среднее квадратическое отклонение по признаку x,
– среднее квадратическое отклонение по признаку x, – среднее квадратическое отклонение по признаку y.
– среднее квадратическое отклонение по признаку y.

 .
.
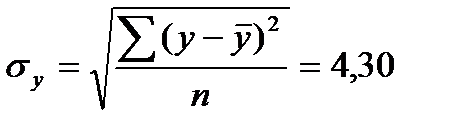 , тогда
, тогда .
. .
. ;
; ;
; ;
; <r<+
<r<+ 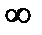 .
. ;
; ;
; ;
;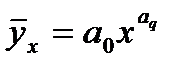 .
. показывает, что:
показывает, что:


