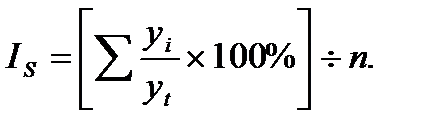Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы анализа основной тенденции развития в рядах динамики и прогнозированиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одной из важнейших задач статистики является определение в рядах динамики основной тенденции развития. Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Для выявления тенденции в рядах динамики используют специальные методы: 1. Метод укрупнения интервалов - предполагает переход от первоначального динамического ряда к рядам с большими временными промежутками, например, данные за каждый месяц года заменяют квартальными, годовые — пятилетними и т.д. По сформированным укрупненным интервалам либо просто суммируют уровни первоначального ряда, либо рассчитывают средние величины. В результате отклонения в уровнях первоначального ряда, обусловленные случайными причинами, сглаживаются, и более явно обнаруживается действие основных факторов (общая тенденция). 2. Метод скользящей средней – состоит в замене фактических значений показателя их усредненными величинами, расчет которых проводят путем последовательного смещения начала отсчета на единицу времени (скольжения), т.е. постепенно исключают из интервала первые уровни и включают последующие. Полученная средняя относится к середине укрупненного интервала. Наиболее часто на практике применяются трехчленные средние:
Полученный таким образом сглаженный ряд более четко выражает основную тенденцию развития изучаемого явления. 3. Метод аналитического выравнивания – заключается в том, что находится уравнение Аналитическое выравнивание позволяет не только определить основную тенденцию развития явления во времени, но и выполнять расчеты для таких периодов, по которым нет информации. При этом нахождение недостающих данных внутри динамического ряда называется интерполяцией, а нахождение значений за пределами анализируемого периода (т.е. в будущем) называется экстраполяцией. Таким образом, на основе экстраполяции данных можно прогнозировать развитие явления в будущем, т.к. такое прогнозирование предполагает, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда. Например, путем аналитического выравнивания получено, что основная тенденция явления выражается уравнением Однако следует помнить, что в действительности тенденция развития того или иного явления не остается неизменной, поэтому полученные путем экстраполяции прогнозируемые значения следует рассматривать как вероятностные оценки. Изучение сезонных колебаний В широком понимании к сезонным относят внутригодовые колебания уровней ряда, имеющие регулярный характер, т.е. более или менее устойчиво повторяющиеся из года в год (в одни и те же месяцы, кварталы и более короткие промежутки времени) изменения уровней ряда в сторону повышения или понижения. Наиболее наглядно они проявляются в таких видах деятельности, как строительство, сельское хозяйство, перевозки пассажирским транспортом и т.п. Сезонные колебания обычно отрицательно влияют на результаты производственной деятельности, вызывая нарушения ритмичности производства. Поэтому регулирование сезонных изменений по отдельным отраслям экономик должно основываться на исследовании сезонных колебаний. Существует целый ряд методов для изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности. Совокупность этих показателей отражает сезонную волну. Порядок расчета индекса сезонности зависит от вида динамического ряда. В стационарных (стабильных) рядах динамики расчет индекса сезонности состоит в определении простой средней арифметической за одни и те же внутригодовые промежутки времени, а затем в сопоставлении полученных средних с общей средней динамического ряда:
где При наличии тренда, т.е. в нестационарных рядах динамики, порядок расчета индекса сезонности следующий: 4) определяют по одноименным внутригодовым уровням ряда (месячным, квартальным) за несколько лет расчетные (выровненные) уровни (yt) при помощи скользящей средней или методом аналитического выравнивания; 5) находят процентное отношение фактических уровней ряда (yi) и расчетных (выровненных) уровней (yt); 6) усредняют полученные показатели сезонности за все годы.
Вопросы для самоконтроля 1. Дайте определение ряда динамики. Из каких элементов он состоит? 2. Какие существуют виды рядов динамики? Приведите примеры. 3. Назовите важнейшее условие правильного построения динамического ряда. 4. Какие показатели анализа рядов динамики Вы знаете? Что они характеризуют? 5. Как определяется средний уровень ряда? 6. Какими наиболее распространенными статистическими методами осуществляется изучение тренда в рядах динамики? 7. Что такое интерполяция и экстраполяция данных? 8. Охарактеризуйте технику прогнозирования на основе экстраполяции данных. 9. Что представляют собой сезонные колебания, в чем практическое значение их изучения? 10. Как исчисляются индексы сезонности? Глава 7. Индексы Цель: усвоить и закрепить материал по теме, приобрести навыки по проведению анализа данных с помощью индексов. Понятие и виды индексов В экономических исследованиях часто приходится сопоставлять не только отдельные признаки, но и сложные явления, состоящие из разнородных элементов, которые непосредственно суммироваться не могут. Изменение таких явлений изучают с помощью индексов. Например, если необходимо дать характеристику изменения объема продукции промышленности. Отдельными элементами в этом случае выступают конкретные виды продукции в натурально-вещественной форме, имеющие разные единицы измерения (т, шт., л, м2 и т.д.), поэтому их не возможно сразу суммировать, сначала нужно найти для них общую меру, например, стоимость продукции. Индекс – это обобщающий показатель, который выражает соотношение величин какого-либо сложного явления во времени, в пространстве или дает сравнение фактических данных с любым эталоном (план, прогноз, норматив и т.д.). С помощью индексов можно определить количественные изменения самых различных показателей развития социально-экономических процессов. Например, в экономике с помощью индексов можно объективно и точно показать изменения в росте или снижении производства, изменения в урожайности, себестоимости и цен выпускаемой продукции, численности работающих, производительности труда, заработной платы, изменение в цене акций на фондовых рынках и пр. В статистике индексы классифицируются по ряду признаков: а) по содержанию изучаемых величин: 3. Индексы количественных показателей – все индексируемые показатели этих индексов являются объемными, т.е. характеризуют общий, суммарный размер (объем) изучаемого явления и выражаются абсолютными величинами. К таким индексам относятся, например, индекс физического объема промышленной продукции, розничного товарооборота, национального дохода и т.д. 4. Индексы качественных показателей – характеризуют уровень явления в расчете на ту или иную единицу совокупности. Например, индекс себестоимости единицы продукции, индекс заработной платы, индекс производительности труда, индексы цен и т.д. Они измеряют не общий объем, а интенсивность, эффективность явления или процесса. б) по степени охвата единиц совокупности: 4. Индивидуальные индексы характеризуют изменение отдельных элементов сложного явления, например, показывает изменение количества или цен по какому-либо одному виду продукции. Он определяется путем деления величины показателя за отчетный период на величину этого же показателя за базисный период. 5. Сводные (общие) индексы отражают изменение всех элементов сложного явления, например, изменение физического объема продукции, включающей разноименные товары. 6. Субиндексы (групповые) используются, если охватываются не все элементы сложного явления, а только их часть, например индексы физического объема продукции по отдельным отраслям промышленности, индексы цен по группам продовольственных и непродовольственных товаров. в) по методам расчета общие индексы делят на: 3. Агрегатные индексы - сложные относительные показатели, которые характеризуют среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной в числителе и знаменателе (вес индекса). 4. Средние из индивидуальных - делятся на арифметические и гармонические и являются производными, т.е. они получаются в результате преобразования агрегатных и индивидуальных индексов. Методы исчисления индексов Для того чтобы рассчитать общий индекс, необходимо преодолеть несуммарность отдельных элементов изучаемого явления, это достигается путем введения в индекс дополнительного неизменного показателя, тесно связанного с индексируемой величиной. Этот показатель называется весом агрегатного индекса. Например, мы хотим узнать, насколько процентов изменился объем производства продукции молочно-консервного завода. Продукция завода может измеряться в л, кг, шт., т.е. возникает несуммарность отдельных элементов продукции. Для того чтобы ее преодолеть физический объем продукции (количество произведенных товаров) умножают на цены. Таким образом, индекс физического объема продукции в качестве весов имеет цены. При выборе веса индекса руководствуются следующим правилом: если индекс количественный, то обычно используют вес базисного периода, а если качественный – то отчетного. В международной статистике для построения индексов применяются следующие обозначения: q – физический объем произведенной продукции (количество); p – цена; z – себестоимость; 1 – отчетный период; 0 – базисный период. Рассмотрим построение самых распространенных индексов (табл. 7.1). Таблица 7.1
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 3236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.217.100 (0.008 с.) |

 .
. , график которого наилучшим образом отражает основную тенденцию ряда динамики.
, график которого наилучшим образом отражает основную тенденцию ряда динамики. . Зная это уравнение и подставляя в него значения t, находящиеся за пределами этого ряда, можно построить прогноз. Пусть t=11, тогда прогнозируемое значение будет равно
. Зная это уравнение и подставляя в него значения t, находящиеся за пределами этого ряда, можно построить прогноз. Пусть t=11, тогда прогнозируемое значение будет равно  .
.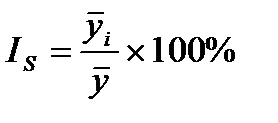 ,
,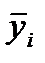 — средний уровень по одноименным внутригодовым отрезкам времени (месяцам, кварталам).
— средний уровень по одноименным внутригодовым отрезкам времени (месяцам, кварталам).