
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы исчисления индивидуальных и сводных индексовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общие индексы показывают, на сколько процентов изменился размер индексируемой величины в отчетном периоде по сравнению с базисным. Для того чтобы рассчитать абсолютное изменение индексируемой величины, необходимо определить разность числителя и знаменателя соответствующего индекса. Например, разность числителя и знаменателя индекса товарооборота показывает, на сколько денежных единиц увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным одновременно за счет изменения объема продаж и цен.
Разность числителя и знаменателя индекса цен показывает экономию (перерасход) покупателей в абсолютном выражении в текущем периоде по сравнению с базисным за счет изменения цен.
Разность числителя и знаменателя индекса физического объема продукции показывает, как в абсолютном выражении изменилась стоимость продукции за счет изменения объема ее производства:
Типовая задача 1 Известны данные о продаже товаров на одном из рынков города:
Определить: 1) изменение цен в отчетном периоде по сравнению с базисным по каждому виду продукции;
2) общее изменение цен на реализованную продукцию в относительном и абсолютном выражении; 3) общее изменение количества реализованной продукции. Сделать выводы. Решение 1) Определим изменение цен в отчетном периоде по сравнению с базисным по каждому виду продукции, т.е. индивидуальные индексы цен.
2) Определим общее изменение цен на реализованную продукцию, т.е. агрегатный индекс цен.
В абсолютном выражении это изменение составило:
Таким образом, из-за повышения цен на продукцию покупатели фактически перерасходовали 494 тыс. руб. 3) Определим общее изменение количества реализованной продукции, т.е. общий индекс физического объема.
Типовая задача 2 Известны данные выпуска продукции строительного предприятия:
Дайте сводную оценку изменения физического объема производства продукции. Решение Определим общее изменение физического объема продукции, т.е. сводный индекс физического объема. Из условия следует, что индивидуальные индексы физического объема по видам продукции имеют следующие значения: - для кирпича: iq = 1,1 или 110%; - для блоков: iq = 0,9 или 90%; - для плит: iq = 0,75 или 75%. Выпуск продукции в I квартале представляет собой произведение q0p0. Таким образом, индекс физического объема определим по формуле средней арифметической.
Индексный метод в статистике применяется также для изучения динамики качественных показателей, уровни которых выражены средними величинами. В этом случае используют систему взаимосвязанных индексов переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава характеризует изменение среднего уровня признака за счет влияния двух факторов: - изменения значения осредняемого признака (х) у отдельных единиц совокупности; - структурных изменений, под которыми понимается изменение доли отдельных единиц совокупности в общей их численности.
Индекс постоянного (фиксированного) состава отражает действие только первого фактора – изменение осредняемой величины, т.е. показывает средний размер изменения изучаемого признака у отдельных единиц совокупности:
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака:
Между указанными индексами существует следующая взаимосвязь:
Типовая задача 3 Известны следующие данные о заработной плате работников по 3 отраслям экономики города:
Определить индексы заработной платы переменного состава, постоянного состава и структурных сдвигов. Решение 1. Для определения индекса заработной платы переменного состава вначале определим средний размер заработной платы по трем отраслям для января и июня.
Определим индекс переменного состава:
Следовательно, средняя заработная плата работников по трем отраслям экономики в июне по сравнению с январем увеличилась на 14%. При этом изменение происходило под влиянием двух факторов: изменения уровня заработной платы в каждой отрасли и изменения структуры численности работников. 2. Вычислим индекс заработной платы постоянного состава:
Таким образом, средняя заработная плата работников по данным отраслям в отчетном периоде по сравнению с базисным увеличилась на 15% в результате изменения только одного фактора – самой заработной платы, без учета структурных изменений численности работников в каждой отрасли. 3. Определим индекс структурных сдвигов:
Следовательно, несмотря на то, что в каждой отрасли в отдельности заработная плата увеличилась, средняя заработная плата работников по трем отраслям вместе уменьшилась на 1% в результате того, что изменилась структура численности работников: увеличилась доля работников с меньшей заработной платой. Задачи для самостоятельной работы Задача 6.1 Известны следующие данные о продаже товаров на рынках города:
Определить: 1) индивидуальные индексы цен объема продажи товаров; 2) общие индексы: а) товарооборота; б) цен; в) физического объема; 3) абсолютное изменение товарооборота по двум товарам вследствие изменения: а) цен; б) объема продажи. Сделать выводы. Задача 6.2 Известны следующие данные о продаже товаров в розничной торговле города:
Определить:
1) индексы физического объема продаж по каждому товару; 2) сводные индексы: физического объема, цен и товарооборота; 3) абсолютный прирост товарооборота за счет изменения: а) цен; б) объема продажи товара. Сделать выводы. Задача 6.3 Затраты на производство продукции на предприятии характеризуются следующими данными:
Определить: 1) общий индекс себестоимости продукции и абсолютный прирост (снижение) затрат в связи с изменением себестоимости единицы продукции; 2) общий индекс физического объема продукции, если известно, что затраты на продукцию за прошедший период возросли на 15,5%. Задача 6.4 Известны данные о продаже товаров в районе:
Определить: 1) общий индекс физического объема; 2) абсолютный прирост стоимости проданных товаров за счет изменения количества продажи товаров. Сделать выводы. Задача 6.5 Известны данные о продаже продуктов в городе:
Определите: 1) общий индекс товарооборота; 2) общий индекс цен: Паше и Ласпейреса, поясните их результаты; 3) общий индекс физического объема; 4) покажите взаимосвязь исчисленных индексов. Задача 6.6 Известны данные об одном из цехов предприятия:
Определите индивидуальные, сводный и средний индекс производительности труда рабочих. Задача 6.7 Известны следующие данные о выпуске одноименной продукции «А» и ее себестоимости по двум предприятиям:
Вычислите: 1) индекс себестоимости переменного состава; 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов. Покажите взаимосвязь между исчисленными индексами. Поясните полученные результаты. Задача 6.8 Известны следующие данные о заработной плате работников предприятий по отраслям экономики:
1. Определите индексы средней заработной платы: а) переменного состава; б) постоянного состава; в) структурных сдвигов. 2. Вычислите абсолютный прирост средней заработной платы вследствие изменения: а) заработной платы в каждой отрасли экономики; б) структуры среднесписочной численности работников. Задача 6.9 Динамика производственных показателей двух предприятий АО, выпускающих одноименную продукцию «А», характеризуются данными:
Определите для двух предприятий: 1) индекс средней себестоимости (индекс переменного состава); 2) среднее изменение себестоимости продукции (индекс постоянного состава); 3) индекс структурных сдвигов; 4) абсолютный прирост средней себестоимости за счет изменения: а) себестоимости продукции на каждом предприятии; б) структуры произведенной продукции. Задача 6.10 Затраты в отчетном периоде по сравнению с базисным увеличились на 8%, общие затраты на производство и продажу продукции в отчетном периоде составляют 659 млн. руб., общий индекс себестоимости равен 0.962. Определить: 1. Себестоимость всей выпущенной продукции в базисном периоде. 2. Индекс количества выпущенной продукции. 3. Абсолютное изменение затрат (себестоимости всей выпущенной продукции) за счет: - количества продукции; - себестоимости единицы продукции; - общее изменение затрат. Тестовые задания 1. Индекс физического объема произведенной продукции =... % (с точностью до 0,1 %) при увеличении объема производства продукции (в стоимостном выражении) на 1,3% и индексе цен, равном 105%. 2. Недостающим элементом в формуле среднего арифметического индекса физического объема товарооборота является:
A. p0q0; B. p1q1; C. q1; D. p1. 3. Агрегатный индекс цен при исчислении по одним и тем же данным будет... среднему (го) гармоническому (го) индексу (а) цен. A. меньше; B. меньше или равен; C. больше; D. больше или равен; E. равен. 4. Агрегатные индексы цен Пааше строятся: A. с весами текущего периода; B. с весами базисного периода; C. без использования весов. 5. При построении агрегатных индексов количественных показателей, используют веса... периода. A. отчетного; B. базисного; C. произвольного. 6. Связь между сводными индексами издержек производства (Izq), физического объема продукции (Iq) и себестоимости (Iz): A. Iq = Izq x Iz; B. Iz = Iq x Izq; C. Izq = Iq x Iz; D. Izq = Iq: Iz. 7. Индекс физического объема продукции составляет... % при условии:
A. 140;
B. 92; C. 132; D. 90. 8. Изменение средней себестоимости однородной продукции по совокупности предприятий оценивается с помощью индекса: A. переменного состава; B. среднего гармонического; C. среднего арифметического; D. агрегатного. 9. Общий индекс себестоимости продукции исчисляется по формуле … при условии:
A. B. C. D. 10. Недостающими числами «m» и «n» в формуле для расчета индекса среднего изменения цен товара «А» (индекса постоянного состава) являются.... при условии:
A. m=200;n=16; B. m=800;n=15; C. m=200; n=17; D. m=300; n=17.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.152.151 (0.01 с.) |


 2) с весами текущего периода:
2) с весами текущего периода:

 2) средний гармонический:
2) средний гармонический:


 2) с весами отчетного периода (по Пааше):
2) с весами отчетного периода (по Пааше):

 2) средний гармонический:
2) средний гармонический:





 2) средний гармонический:
2) средний гармонический:


 2) средний гармонический:
2) средний гармонический:






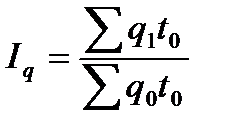


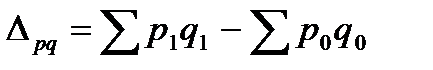

 .
. или 103%, т.е. цены на товар А в отчетном периоде по сравнению с базисным увеличились на 3%.
или 103%, т.е. цены на товар А в отчетном периоде по сравнению с базисным увеличились на 3%. или 104%, т.е. цены на товар Б в мае по сравнению с апрелем повысились на 4%.
или 104%, т.е. цены на товар Б в мае по сравнению с апрелем повысились на 4%. или 110%, т.е. цены на товар В отчетном периоде по сравнению с базисным увеличились на 10%.
или 110%, т.е. цены на товар В отчетном периоде по сравнению с базисным увеличились на 10%. или 107%, т.е. в относительном выражении цены на всю реализованную продукцию в мае по сравнению с апрелем в среднем увеличились на 7%.
или 107%, т.е. в относительном выражении цены на всю реализованную продукцию в мае по сравнению с апрелем в среднем увеличились на 7%. (тыс. руб.)
(тыс. руб.) или 86%, т.е. объем реализованной продукции в среднем в отчетном периоде по сравнению с базисным снизился на 14%.
или 86%, т.е. объем реализованной продукции в среднем в отчетном периоде по сравнению с базисным снизился на 14%. или 90%, т.е. объем производства во втором квартале по сравнению с первым уменьшился на 10%.
или 90%, т.е. объем производства во втором квартале по сравнению с первым уменьшился на 10%. .
. .
. .
. .
. - средняя заработная плата в январе;
- средняя заработная плата в январе; - средняя заработная плата в июне.
- средняя заработная плата в июне. или 114%.
или 114%. или 115%.
или 115%. или 99%.
или 99%. .
. ;
; ;
; ;
;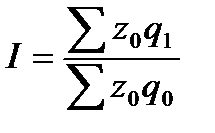 .
. .
.


