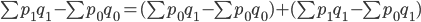Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индивидуальный индекс товарооборотаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Индивидуальный индекс товарооборота характеризует изменение товарооборота по одному товару и строится как отношение товарооборота отчетного периода
Разница между числителем и знаменателем его покажет абсолютное изменение товарооборота в рублях за счет двух фактров: изменения количества проданного товара и изменения цены этого товара, то есть Рассчитаем индивидуальные индексы товарооборота (10): По телевизорам: По видеомагнитофонам: Рассмотренные нами индивидуальные индексы взаимосвязаны между собой так же, как сами индексируемые показатели: индекс товарооборота равен произведению индекса физического объема товарооборота на идекс цен, то есть Проверим взаимосвязь исчисленных индивидуальных индексов: § По телевизорам: 0,99 = 0,9*1,1 § По видеомагнитофонам: 1,125 = 1,25*0,9 Кроме того, полученные данные позволяют рассчитать абсолютные показатели изменения товарооборота по отдельным товарам за счет отдельных факторов. Так, по телевизорам общее изменение товарооборота составило: 1. за счет изменения количества проданных товаров: 2. за счет изменения цен: Проверим взаимосвязь исчисленных показателей: По видеомагнитофонам имеем изменение товарооборота на 50 млн.руб. 1. за счет изменения количества проданных товаров: 2. за счет изменения цен: Товарооборот по видеомагнитофонам увеличился на 50 млн.руб. За счет увеличения количества проданных видеомагнитофонов на 50 тыс.штук товарооборот возрос на 100 млн.руб, а за счет снижения цен на видеомагнитофоны на 0,2 тыс.руб за штуку стал меньше на 50 млн.руб.
31.Общие индексы, необходимость их применения Все рассмотренные индексы характеризуют относительное изменение уровней отдельных элементов явления и называются индивидуальными индексами. Однако большинство изучаемых статистикой общественных явлений и процессов состоят из многих элементов, которые могут быть как однородными, так и неоднородными. Однородные явления можно непосредственно суммировать и исчислять индексы, характеризующие изменение не одного элемента, а группы элементов или всей совокупности в целом. Такие индексы называются общими индексами. Так, можно суммировать количество проданных однородных товаров по группе фирм и исчислить общий индекс физического объема товарооборота по формуле:
Если же отдельные элементы явления неоднородны, то непосредственное суммирование их невозможно или бессмысленно и тогда необходимо привести их к сопоставимому виду. Все товары имеют стоимость, а стоимости товаров можно суммировать. Переход от натуральных показателей к стоимостным позволяет преодолеть несуммарность натурально-вещественных элементов совокупности. Но изменение стоимости товаров обусловлено совместным изменением двух факторов — количества товаров и цен на них, а нам необходимо определить изменение каждого из этих факторов в отдельности. Для изучения изменения одного фактора необходимо абстрагироваться от изменения второго, взаимосвязанного с ним фактора и построить общий индекс в агрегатной форме. Так, агрегатный индекс физического объема товарооборота должен показать изменение количества проданных разнородных товаров, поэтому в числителе его берется отчетное количество товаров (q1), а в знаменателе — базисное (q0), т.е. индексируемый показатель изменяется, а взвешивание производится в одних и тех же ценах базисного период (p0):
В числителе этого индекса — условная величина товарооборота отчетного периода в ценах базисного периода, в знаменателе — реальная величина товарооборота базисного периода. Разность между числителем и знаменателем индекса покажет абсолютное изменение товарооборота за счет изменения физического объема товарооборота:
Рассчитаем агрегатный индекс физического объема товарооборота по данным нашего примера:
Агрегатные индексы качественных показателей строятся при весах — объемных показателях отчетного периода. Так, агрегатный индекс цен по формуле немецкого экономиста Э.Пааше:
В числителе индекса — товарооборот отчетного периода, в знаменателе — товарооборот отчетного периода в ценах базисного периода, а разность между ними характеризует: с позиции продавца — абсолютное изменение товарооборота за счет изменения цен, с позиции покупателя — экономию (перерасход) населения от изменения цен на товары: Рассчитаем агрегатный индекс цен по данным нашего примера:
В качестве весов в индексах качественных показателей могут быть использованы не только абсолютные объемные показатели, но и показатели их структуры, то есть доли. В статистической практике используется также индекс цен, построенный с базисными весами по формуле Э.Ласпейреса:
Агрегатный индекс товарооборота исчисляется по формуле:
Агрегатные индексы объемных и качественных показателей, построенные с различными весами, взаимосвязаны между собой так же, как индивидуальные индексы: произведение агрегатного индекса физического объема товарообора на агрегатный индекс цен, дает агрегатный индекс товарооборота:
Мы получили систему взаимосвязанных агрегатных индексов, каждый из которых позволяет определить изменение индексируемого показателя в относительном выражении (%). Кроме того, по этим индексам можно определить изменение обобщающего показателя — товарооборота за счет отдельных факторов в абсолютном выражении как разность между числителем и знаменателем соответствующего индекса. Абсолютные показатели изменения товарооборота за счет отдельных факторов взаимосвязаны следующим образом.
Проверим взаимосвязь показателей, исчисленных по данным нашего примера: 1. аграгатных индексов: 1,024 = 0,975*1,037 2. абсолютных изменений: +38 млн.руб = — 20 + 58 млн.руб. Аналогичным образом строятся системы агрегатных индексов других экономических показателей.
и Общий (сводный) индекс характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми. В зависимости от способа изучения общие индексы могут быть построены или как агрегатные (от лат. аggrega - присоединяю) индексы, или как средние взвешенные индексы (средние из индивидуальных). Способ построения агрегатных индексов заключается в том, что при помощи так называемых соизмерителей можно выразить итоговые величины сложной совокупности в отчетном и базисном периодах, а затем первую сопоставить со второй.
32.Правило построения индексов Труднейший вопрос при построении индекса — выбор его весов и возможно В зависимости от методологии расчета общие и групповые индексы подразделяются на агрегатные (суммарные) и средние из индивидуальных индексов. 33.Средние индексы В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса, т. е. он может быть преобразован в средний арифметический и средний гармонический индексы. Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне объяснима: ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и, конечно, его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу. Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов. Например, известен индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0 p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема:
(агрегатная форма индекса Ласпейреса). Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс:
Тогда формула сводного индекса примет вид:
т. е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде. Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (г^) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:
Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq, тогда:
таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема. Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован и рассчитан как средний из индивидуальных индексов только при совпадении перечня видов продукции или товаров (их ассортимента) в отчетном и базисном периодах, т. е. когда агрегатный индекс построен по сравнимому кругу единиц (агрегатные индексы качественных показателей и агрегатные индексы объемных показателей при условии сравнимого ассортимента).
34.Индексы переменного, постоянного состава и структурных видов
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 756; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.168.219 (0.01 с.) |

 к товарообороту базисного периода
к товарообороту базисного периода  , то есть по формуле:
, то есть по формуле:

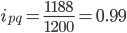 или 99% и
или 99% и  млн.руб, то есть товарооборот по телевизорам стал меньше на 12 млн.руб, или на 1% (99-100%).
млн.руб, то есть товарооборот по телевизорам стал меньше на 12 млн.руб, или на 1% (99-100%). или 112.5% и
или 112.5% и  млн.руб, то есть товарооборот по видеомагнитофонам увеличился на 50 млн.руб. или на 12,5% (12,5-100%).
млн.руб, то есть товарооборот по видеомагнитофонам увеличился на 50 млн.руб. или на 12,5% (12,5-100%).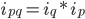
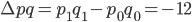 млн.руб, то есть товарооборот по телевизорам в отчетном периоде по сравнению с базисным стал меньше на 12 млн.руб. Эта величина может быть разложена на две:
млн.руб, то есть товарооборот по телевизорам в отчетном периоде по сравнению с базисным стал меньше на 12 млн.руб. Эта величина может быть разложена на две: млн.руб, то есть за счет уменьшения количества проданных телевизоров на 40 тыс.штук товарооборот стал меньше на 120 млн.руб.
млн.руб, то есть за счет уменьшения количества проданных телевизоров на 40 тыс.штук товарооборот стал меньше на 120 млн.руб. млн.руб, то есть за счет роста цены одного телевизора на 0,3 тыс.руб товарооборот возрос на 108 млн.руб.
млн.руб, то есть за счет роста цены одного телевизора на 0,3 тыс.руб товарооборот возрос на 108 млн.руб. млн.руб.
млн.руб.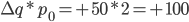
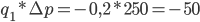
 , где знак
, где знак  означает суммирование данных о количестве одного товара по нескольким фирмам. Можно суммировать товарооборот по нескольким товарам и исчислять общий индекс товарооборота по формуле
означает суммирование данных о количестве одного товара по нескольким фирмам. Можно суммировать товарооборот по нескольким товарам и исчислять общий индекс товарооборота по формуле  , где знак
, где знак  .
.
 или 98,75% и
или 98,75% и  млн.руб., то есть количество проданных магазином товаров в среднем стало меньше на 1,25% (98,75 — 100%), что привело к уменьшению товарооборота на 20 млн.руб.
млн.руб., то есть количество проданных магазином товаров в среднем стало меньше на 1,25% (98,75 — 100%), что привело к уменьшению товарооборота на 20 млн.руб.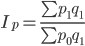
 .
.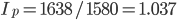 или 103.7% и
или 103.7% и 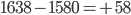 млн.руб, то есть в среднем цены на товары возрасли на 3,7%, что привело к росту товарооборота на 58 млн.руб.
млн.руб, то есть в среднем цены на товары возрасли на 3,7%, что привело к росту товарооборота на 58 млн.руб.
 или 102.4%. Разность между числителем и знаменателем этого индекса характеризует абсолютное изменение товарооборота за счет двух фактров: изменения количества проданных товаров и цен на них:
или 102.4%. Разность между числителем и знаменателем этого индекса характеризует абсолютное изменение товарооборота за счет двух фактров: изменения количества проданных товаров и цен на них:  млн.руб, то есть товарообот в отчетном периоде по сравнению с базисным увеличился на 38 млн.руб. или на 2,4%.
млн.руб, то есть товарообот в отчетном периоде по сравнению с базисным увеличился на 38 млн.руб. или на 2,4%.