
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сводные индексы переменного, постоянного (фиксированного) состава и структурных сдвиговСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
I.Сводный индекс переменного состава характеризует изменение средней величины качественного показателя по всей совокупности. К качественным показателям можно отнести себестоимость, цену за единицу продукции, производительность, продуктивность животных, урожайность. Качественные показатели имеют сложные единицы измерения и представляют собой сопоставление двух показателей, имеющих разное содержание, т. е. разные значения признака: руб./кг, руб./шт., шт.(ед.)/час, л(ц)/1гол., т/га, кватт/час Например, индекс средней цены показывает на сколько % средняя цена изменяется в отчетном периоде по сравнению с базисным:
Индекс переменного состава равен произведению индекса постоянного состава на индекс структурных сдвигов:
II.Сводный индексфиксированного (постоянного) состава характеризует изменение величины качественного показателя в среднем по отдельным объектам совокупности. Например, изменение общей средней цены за счет изменения индивидуальных цен в отчетном периоде по сравнению с базисным:
III.Индекс структурных сдвиговпоказывает изменение средней величины анализируемогокачественногопоказателя за счет изменения структуры количественногопоказателя: физического объема продукции (ассортимента продукции). Положительным показателем индекса структурных сдвигов является величина, равная или больше единицы (1). Например, изменение средней цены в отчетном периоде за счет изменения физического объема:
Пример расчета сводных индексов:
1. Сводный индекс переменного состава это общий индекс средней продуктивности, характеризует изменение средней продуктивности по отдельным группам:
что в абсолютном выражении составило: ∆Ῡ=33,7-30,5= +3,2(ц/кор.) в том числе: 1. за счет изменения продуктивности коров – это отношение двух средних уровней продуктивности, но при условии неизменной возрастной структуры стада. Рассчитывается сводный индекс постоянного (фиксированного) состава:
2. за счет изменения структуры поголовья (исключено влияние продуктивности отдельных животных) – рассчитывается сводный индекс структурных сдвигов:
Индекс структуры больше 1 свидетельствует о положительной структуре анализируемого показателя, в нашем примере <1, что привело к снижению средней продуктивности. Иными словами: в структуре стада имелись животные с низкой продуктивностью. Общее изменение:
Взаимосвязь этих индексов:
2. Общий индекс валовой продукции:
3. Общий индекс численности поголовья:
Взаимосвязь этих индексов:
35.Расчёт агрегатных индексов с переменными и постоянными весами При изучении динамики экономических явлений строятся и исчисляются индексы рядов последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексе сравнение индексируемого показателя в каждом индексе производится с уровнем одного и того же периода, а в ряду цепных индексов индексируемый показатель сопоставляется с уровнем предыдущего периода. В каждом отдельном индексе веса в его числителе и знаменателе обязательно фиксируются на одном том же уровне. Если же строится ряд индексов, то вес в нем могут быть либо постоянными для всех индексов ряда, либо переменными. Ряд базисных индексов объема продукции:
Постоянные веса (р 0) имеет и ряд цепных индексов:
Ряд цепных индексов цен:
Для индексов динамики с постоянными весами имеет силу взаимосвязь между цепными и базисными темпами роста (индексами):
Использование постоянных весов в течение ряда лет позволяет переходить от цепных индексов к базисным, и наоборот. Поэтому ряды индексов объема продукции и объема проданных товаров строятся в статистической практике с постоянными весами. Так, в индексах объема продукции в качестве постоянных весов используются цены, зафиксированные на уровне, который был установлен на 1 января какого-либо базисного года. Такие цены, используемые в течение ряда лет, называются сопоставимыми (фиксированными). Использование в индексах объема продукции (товаров) сопоставимых цен позволяет путем простого суммирования получать итоги за несколько лет. Сопоставимые цены не должны сильно отличаться от действующих (текущих). Чтобы иметь возможность исчислять индексы объема продукции за длительные периоды, в течение которых применялись различные сопоставимые цены, продукцию одного года оценивают как в прежних, так и в новых фиксированных ценах. Индекс за длительный период исчисляют цепным методом. 36.Территориальные индексы Территориальные индексы представляют собой разновидность относительных величин сравнения, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям, государствам). На основе территориальных индексов выполняются международные сопоставления. Территориальный индекс товарооборота — это отношение суммы выручки от продажи в одном из районов к аналогичному показателю в другом. Один из районов (например, Б) берется за базу сравнения т.е.
Различие объемов товарооборота вызвано различием ассортимента и количества проданных товаров, а также цен. Территориальный индекс физического объема товарооборота рассчитывается по следующей формуле:
где р — средняя межрайонная цена товара каждого вида,
Территориальный индекс цен определяется:
где q - суммарный по двум районам объем продаж каждого вида товара.
Такие сложные взвешивающие показатели применяются для того, чтобы результаты расчета были обратимыми, т. е. чтобы выполнялись соотношения:
Условия индексной модели могут нарушаться, хотя и не очень существенно. Использование таких территориальных индексов для анализа абсолютной разницы товарооборотов дает в только приближенный результат. Территориальные индексы можно также рассчитывать: § с использованием соизмерителей только района А или только района Б; § как среднюю геометрическую из двух территориальных индексов, рассчитанных с разными территориальными весами.
37.Асимметрия: левосторонняя и правосторонняя Различают следующие разновидности кривых распределения: Для однородных совокупностей, как правило, характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп. Выяснение общего характера распределения предполагает оценку его однородности и вычисление показателей асимметрии и эксцесса. Для симметричных распределений частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Рассчитанные для таких распределений средняя, мода и медиана так же равны.
Рис. 2. Левосторонняя асимметрия Центральными называются моменты распределения, при вычислении которых за исходную величину принимаются отклонения вариантов от средней арифметической данного ряда. Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной, если она меньше 0,25, то – незначительной.
Среднеквадратическая ошибка эксцесса (σEk) рассчитывается по формуле:
38.Графическое изображение рядов распределения Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку. Различают атрибутивные и вариационные ряды распределения. Атрибутивный – это ряд распределения, построенный по качественным признакам. По количественному признаку строится вариационный ряд распределения. Он состоит из частоты (численности) отдельных вариантов или каждой группы вариационного ряда. Данные числа показывают, насколько часто встречаются различные варианты (значения признака) в ряду распределения. Сумма всех частот определяет численность всей совокупности. В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды распределения. В дискретном вариационном ряде распределения группы составлены по признаку, изменяющемуся дискретно и принимающему только целые значения. В интервальном вариационном ряде распределения группировочный признак, составляющий основание группировки, может принимать в определенном интервале любые значения. Вариационные ряды состоят из двух элементов: частоты и варианты. Вариантой называют отдельное значение варьируемого признака, которое он принимает в ряду распределения. Частота – это численность отдельных вариант или каждой группы вариационного ряда. Если частоты выражены в долях единицы или в процентах к итогу, то их называют частостями. Плотность распределения – это отношение числа единиц совокупности к ширине интервала. Анализ рядов распределения можно проводить на основе их графического изображения. Линейчатые и круговые диаграммы строятся для отображения структуры совокупности. Применяются вместе с диаграммами и такие линии, как полигон, кумулята, огива, гистограмма. Полигон
Гистограмма
Полигон – ломаная кривая, строится на основе прямоугольной системы координат, когда по оси Х откладываются значения признака, а по оси У – частоты. Гладкая кривая, соединяющая точки – это эмпирическая плотность распределения. Кумулята – ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси Х откладываются значения признака, а по оси У – накопленные частоты. Для дискретных рядов на оси откладываются сами значения признака, а для интервальных – середины интервалов. На основе гистограмм можно строить диаграммы накопленных частот с последующим построением интегральной эмпирической функции распределения.
39.Виды и формы связи
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.161.178 (0.008 с.) |










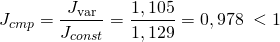












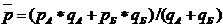


 и
и 
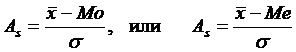 , где Mo, Me – модальное (медианное) значение переменной x.
, где Mo, Me – модальное (медианное) значение переменной x. 

 .
. .
.  .
. , где п – число наблюдений
, где п – число наблюдений 





