Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индексы переменного состава, постоянного состава и структурных сдвигов.Содержание книги
Поиск на нашем сайте
Индексы позволяют анализировать изм-ия не только агрегатов, но и сред. вел. Предпол. изучается динамика сред. цены товара А на неск. рынках. На сред. цену продажи влияют не только цены на каждом из рынков, но и объемы продаж на каждом из них в общем объеме. Изменение сред. цены выраж. индексом: Далее анализ влияние каждого из этих фак-ов на изменение ср цены. С этой целью расчитыв индекс постоянного состава: Данный индекс показ влияние изменений уровней цен по отдел рынкам на изменение средней цены. Индекс структурных сдвигов: Данный индексный анализ позволяет проанализ изменение средней цены в абсолютном выражении. Средняя цена базис.пер-д а: Сред.цена отчет.пер-да: Сред.цена базис.пер-да при структ.отчет.пер-да: Абсол.измен.цены в целом: Индексир метод изуч влияния факторов последовательно-цепной подстановки При построении сводных индексов, входящих в систему, возникает вопрос, на весах какого периода д.б. построен тот или иной индекс. Для этого определим индексируемый признак – признак, изменение которого характеризует данный индекс. Признак-вес – выполняет функцию веса по отношению к индексируемому признаку. Его значение в данном индексе не изменяется, т.к. он не должен искажать оценку изменения индексируемого признака. При определении периодов весов следует руководствоваться правилом: индексы первичных признаков строятся на весах баз. периода, а индексы вторичных признаков – на весах отчетного периода. Приведем пример:у=а·в Тогда сводный индекс у след:
Предположим, что а-первичный признак, а в-вторичный признак Тогда сводный индекс у под влиянием признака а след:
А сводный индекс у под влиянием признака в след:
Территариальные индексы Терр индексы служат для сравнения показателей в пространстве, т.е. по п/п, округам, городам, районам и пр. Построение терр индексов опр выбором базы сравнения и весов или уровня, на кот фиксир веса. При двусторонних сравнениях каждая терр может быть и сравниваемой (числитель индекса), и базой сравнения (знаменатель). Веса, как первой, так и второй терр в принципе также имеют равные основания использ при расчете индекса. Однако это может привести к различным или даже противореч рез-м. Избежать подобной неопределенности можно несколькими способами. Один из них заключ в том, что в кач-ве весов приним объемы проданных т-ов по двум регионам, вместе взятым: 2-ой способ расчета заключ в том, что сначала рассчи ср цены на т-ры по двум терр вместе:
После этого рассчит терриндекс цен:
Различают два типа связей между различн явлен и их призн: функцион и статистич. Функц связи хар полным соответствием м/у изменением факторного призн и изменен результ величины, и каждому знач призн-фактора соответ определен знач результат призн. Стат связи проявл в том, что при измен знач фактора измен распредел результат призн. При стат связи разным значениям одной переменной (фактора х) соответ разные распределения другой переменной (результата у). Корреляц связь — частный случай стат связи, при кот разным знач переменной соответ разные ср значения др переменной. Корреляц связь предполаг, что изучаемые переменные имеют колич выражение, стат связь – более широкое понятие и не включает ограничений на уровень измерения показателей. Корреляц связь может возникать разными способами: причинно-следственные связи, связи соответствия, т.е. сопряж изменение двух признаков, оба признака могут быть и причиной, и следствием. Сущ два базовых инструмента, с п-ю кот анализ двумерные данные: корреляционный анализ, позвол оценить степень взаимосвязи между двумя факторами, и регрессионный анализ, показ, как можно предсказать или управлять одной из двух переменных с помощью другой. Проверка стат гипотез позвол оценить взаимосвязь, кот, как кажется, сущ в изучаемых данных, и выяснить, явл ли она значимой или может быть объяснена исключительно случайностью. Цели кореляц-регресс анализа: 1. Описание и понимание взаимосвязи. Это самая общая цель, обеспеч получение базовой инфо. При изучении сложной с-мы очень важно знать, какие факторы наиболее тесно взаимодейст друг с другом, а какие вообще не оказ влияния друг на друга. Знание этой инф может оказать помощь в долгоср планир и принятии стратегич решений. 2. Прогнозир и предсказание нового наблюд. Понимание взаимосвязи позволяет использ инф об одном из измерений для более качеств предсказания другого измерения. Если, например, известно, что в этом квартале кол-во заказов на продукцию увелич, можно ожидать и увелич объема сбыта. Если вы проанализировали взаимосвязь между количеством заказов и объемами сбыта в прошлом, у вас есть все шансы сделать достоверный прогноз сбыта на будущее, основываясь на текущем количестве заказов. 3. Регулир и управление пр-ом. При вмешив в какой-либо процесс, необходимо опр объем этого вмешательства. Если сущ взаимосвязь между вмешательством и результатом и эта взаимосвязь понятна, то такое знание поможет выполнить оптимальное регулирование.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.148 (0.008 с.) |

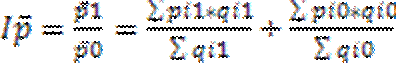 Это индекс переменного состава, т.к. отражает не только измен осредненного признака, но и ст-ры совокупности. Индекс пер.сост. оценивает изм-ие сред.цены под влиянием 2-х факторов: 1)изм-ие уровней цен на отд.рынках; 2)изм-ие ст-ры продаж.
Это индекс переменного состава, т.к. отражает не только измен осредненного признака, но и ст-ры совокупности. Индекс пер.сост. оценивает изм-ие сред.цены под влиянием 2-х факторов: 1)изм-ие уровней цен на отд.рынках; 2)изм-ие ст-ры продаж.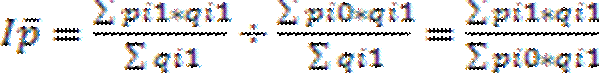
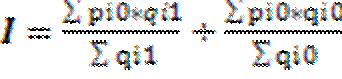
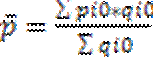
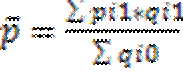
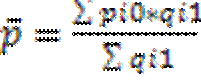 ;
;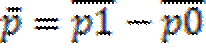
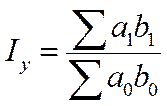

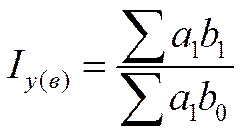
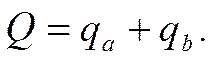 Терр индекс цен в этом случае рассчит по ф-ле:
Терр индекс цен в этом случае рассчит по ф-ле: 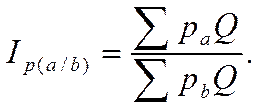
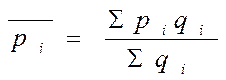 .
.