
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные задачи индексного метода. Индивидуальный и сводные индексы.Содержание книги
Поиск на нашем сайте
Необходимость … потребностями общества в учете, контроле и анализе динамики цен. Задачи: - Оценка динамики обобщающих показателей, характеризующих разнородные совокупности; - Анализ фактора на изменение результативной …; - Анализ влияния структурных видов на изменение средних показателей по однородной совокупности; - Территориальный, в том числе международные сравнения. Индекс – представляет собой относительный показатель, который характеризует изменение сложного экономического явления во времени, в пространстве или по сравнению с некоторым эталоном (с планируемым или нормативным уровнем). Опр.: Индекс – относительная величина, которая показывает во сколько раз уровень изучаемого явления в одних условиях того же явления в других условиях. По охвату единиц совокупности индексы делятся на индивидуальный и сводный. I Индивидуальные индексы – характеризуют динамику или территориальные изменения по одному товару, одному виду продукции, одной сельскохозяйственной культуре. Расчет и анализ данных индексов позволяет сделать комплексный вывод по всей изучаемой совокупности, в которые включены несколько несоизмеримых товаров или видов продукции. 1. Индивидуальный индекс цены
p1 – цена товара в текущем периоде; р0 - цена товара в базисном периоде.
2. Индивидуальный индекс физического объема производства (реализации).
q1 – количество товара, произведенное (реализованное) в текущем периоде; q0 – количество товара, произведенное (реализованное) в базисном периоде.
3. Индивидуальный индекс товарооборота.
Замечание:
Вывод: Таким образом, изменения товарооборота складывается под воздействием динамики цены и изменения объема продажи. II Сводные индексы – вычисляются по товарным группам или нескольким видам продукции, т.е. выпускаемой одним предприятием или всеми предприятиями отрасли (несколько сельскохозяйственных культур) Сводные индексы могут быть представлены в: - агрегатной форме - среднеарифметической форме - среднегармонической форме Агрегатная форма сводных индексов. Сводные индексы в агрегатной форме цен, товарооборота, физического объема реализации. Примеры. Исходной формой выражения сводного индекса является агрегатная форма. Сводный индекс товарооборота.
Если n – число товаров, входящих в товарную группу, то данный индекс:
Пример. Реализация мясных продуктов.
Ноябрь: цена 1 кг, руб - продано, т - Декабрь: цена 1 кг, руб продано, т -
Вывод: товарооборот в целом по данной товарной группе в текущем периоде(декабре) по сравнению с базисным (ноябрь) уменьшился на 8,62 % На величину индекса товарооборота оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того, чтобы оценить изменение только цен индексируемой величины необходимо количество проданных товаров (веса индексов) зафиксировать на каком-нибудь постоянном уровне. При исследовании таких показателей как цена, себестоимость, производительность труда, урожайность, количественный показатель обычно фиксируют на уровне текущего периода. Сводный индекс цен по методу Пааше.
Пример.
Вывод: по данной товарной группе цены в декабре по сравнению с ноябрем выросли в среднем на 2,81 %. Числитель – сумма денег, фактически уплаченная покупателям в текущем периоде за приобретенные товары. Знаменатель показывает, какую сумму покупатель заплатил бы за те же товары, если бы цены не изменились.
В нашем примере: E= 2756000 рублей. Сводный индекс цен по методу Ласпейреса.
Сводный индекс физического объема реализации.
Индексы затрат на производство, индексы себестоимости, индексы физического объема продукции.
Средние формы сводных индексов. Примеры. Любой сводный индекс можно представить, как среднюю взвешенную из индивидуальных индексов. Имеем индивидуальный индекс
Рассмотрим индекс сводный
Пример. Изменение товарооборота.
Требуется получить сводную оценку изменения цен. Вычислим среднегармонический индекс цен (товарооборот сократим на 100).
Вывод: цены по данной товарной группе в текущем периоде по сравнению с базисным в среднем возросли на 2,86%. Просчитаем сводный индекс по методу Ласпейреса.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.006 с.) |












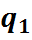








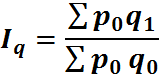









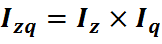


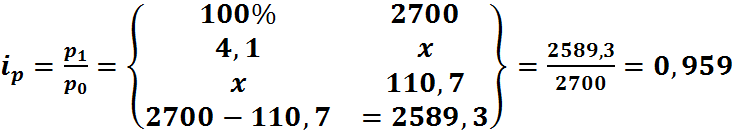 (Для D; также для E,F)
(Для D; также для E,F)





