
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие абсолютных и относительных величин в статистикеСодержание книги
Поиск на нашем сайте
В статистике выделяют 4 группы статистических показателей: 1.Абсолютные показатели(абс. величины)-первичные сведения,полученные о единстве совокупности и совокупности в целом. Абсолютная величина-количественный показатель объема или размера изучаемого признака,всегда имеет определенную единицу измерения(натуральную,денежную,трудовую).Делится на: а)моментный(индивидуальный)показатели,которые характеризуют накопленный результат на определенную дату; б)интервальный(суммарный)показатели,которые характерезуют накопленный результат за период времени(число родившихся или умерших) 2.Относительные показатели(относительные величины)-образуют систему взаимосвязанных статистических показателей. Относительные показатели-это обобщенный показатель,дающий числовую меру соотношения двух сопоставленных абсолютных величин(при расчете абс. величин числитель называется текущей или сравниваемой,а знаменатель называется базой сравнения или основанием) Если за базу сравнения принять 100 ед. относительная величина выражается в %. Если за базу сравнения принять 1000 ед. относительная величина выражается в ‰. Выделяют виды относительных величин: 1)Относительный показатель динамики(ОПД)-характеризует изменения уровня развития какого-либо явления во времени,полученные в результате деления уровня признака в определенный период или момент времени на уровень этого же показателя в предшествующий период.
2007 г.(факт)-100 тыс. т. 2008 г.(факт)-80 тыс. т. 2008 г.(план)-120 тыс. т. ОПД=80/100=0,8-коэффициэнт; 0,8*100%=80%(товарооборот уменьшился на 20% по сравнению с прошлым годом) 2)Относительный показатель плана(ОПП)-характеризует отношение уровня запланированного на предстоящий уровень
ОПП=120/100=1,2; 1,2*100 3)Относительный показатель реализации плана(ОПРП)
ОПРП=80/120=0,7; 0,7*100%=70%(недовыполнение плана в 2008 г. На 30%) Между показателями существует связь. ОПП*ОПРП=ОПД 4)относительный показатель структуры(ОПС)-характеризуют доли,удельные веса составных элементов в общем итоге ОПС= 5)Относительный показатель координации(ОПК)
В качестве базы сравнения выбирают либо группу, имеющую самый большой удельный вес или самое наибольшее значение Импорт – 500 ед.; Экспорт – 400 ед.(база) ОПК=500/400=1,25 Импорт превосходит экспорт в 1,25 раз,т.е. характеризует отношение частей данной совокупности к одной из них,которая принимается за базу ОПК показывает во сколько раз одна часть совокупности больше другой,либо сколько ед. одной части приходиться на 1,100,1000 и т.д. ед. другой части 6)Относительный показатель интенсивности(ОПИ)
Количество населения – 300 000 чел.,территория – 1 000 км2 ОПИ=300 000 чел./1 000км2=300 чел/км2 7)Относительный показатель средний(ОПср.)
Характеризует сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду, либо моменту времени, но к различным объектам или территориям. 12) средние величины. примеры Средняя величина-обобщающий показатель, характеризующий типический уровень явления Он выражает величину признака, отнесенные к ед. совокупности. Средние величины: 1)степенные средние 2)структурные средние Степенные средние: 1)среднегармоническое 2)среднегеометрическое 3)среднеарифметическое 4)среднеквадратическое 5)среднекубическое Виды степенных средних
Если расчет по несгруппированным,то простые степенные средние
Если сгруппировать данные, то взвешенная средняя вычисляется Пусть необходимо развести перегруппировку данных,образовав новые группы с интервалами до 500,от 500-1000, 1000-2000, 2000-3000, 3000 и более. Распределение работников строительной фирмы. По уровню дохода.
Структурные средние. Примеры В качестве структурных средних используют показатели моды-наиболее часто повторяющиеся значения признака и медианы-величины признака,которая делит упорядоченную совокупность,на две равные по численности части. для интервального ряда расчет моды и медианы:
Mo=
Показатели вариации. Примеры В статистике существует несколько способов для измерения вариации.Наиболее простым является расчет показателя размаха вариации: R Более строгими характеристиками являются показатели колеблимости относительно среднего уровня. Простейший показатель такого признака-среднее линейное отклонение:
Дисперсия( σ2= 𝜎= Если первичные данные сгруппировать,то дисперсия признака может быть определена по следующей формуле:
Имеются данные об объеме выполненных работ. Организациями на предприятиях разных форм собственности
1. Определить средний объем выполнения работ на предприятии 2-ух форм собственности
2. Определить средний объем предприятия каждой формы собственности
3. Рассчитать внутригрупповую и общегрупповую дисперсию
(Общая дисперсия)
Групповая дисперсия
4. Рассчитать среднее из внутригрупповых дисперсий.
7 338 180=815 264+6 522 916
η2= η2 стремится к 100%;он показывает,что дисперсия выполненных работ зависит от формы собственности предприятия на 88,9%,а остаток 11,1% определяется множеством неучтенных факторов.
Из этого следует мы можем утверждать,что существует тесная связь между формой собственности предприятия и объемом выполненной работы Для расчета существенности связей между группированным признаком(форма собственности) и вариации(изменчивостью)исследуемого признака(объем выполненных работ)используем критерий Фишера
к=m-1
То наличие связи доказано
При расчете относительных показателей вариации базой для сравнения служат среднее арифметическое ( К ним относятся:
Замечание:если 15) Моменты распределения. Показатели асимметрии и … Моменты распределения. Одной из важных задач рядов распределения является выявление закономерностей распределения определенных ее характеристик и количественного выражения.Эта задача решается при помощи не дописано, характеризующих форму, тип распределения. Важной характеристикой рядов распределения являются моменты распределения. Моментом распределения называется число, которое вычисляется по формуле:
В начальные моменты используются
Если все наблюдаемые значения выборки увеличиваются(уменьшаются) на одно и тоже число,то центральный выборочный момент k не изменяется
Если все наблюдаемые значения умножить на одно и тоже число С, то Кривая распределения-линия на плоскости,отражающая зависимость между значениями признака и соответствующие им не дописано.
Эмпирическая кривая-это фактическая кривая распределения полученная по данным наблюдения и отражающиеся как общие так и случайные условия,определяющие распределения. Теоретическая кривая-кривая,выражающая функциональную связь между изменением варьирующего признака и изменения частот и характеризующая определенный тип распределения. Анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического сопоставления. Нормальное распределение имеет следующую функцию: f(x)= 𝜎
Для нормальных распределений характерны следующие разновидности: 1. Одновершинные кривые-характерные показатели ассиметрии As
Если As As As=0,то не дописано. As As Ех=
2. Многовершинные распределения Одновершинное распределение говорит об однородности совокупности. Многовершинное говорит о неоднородности совокупности, показывая необходимость перегруппировки данных.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.149 (0.006 с.) |

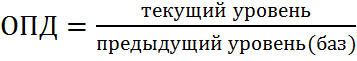

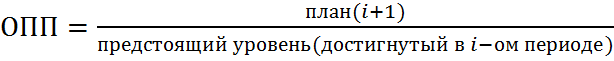

 =120%(товарооборот увеличился на 20% не дописано )
=120%(товарооборот увеличился на 20% не дописано )
 *100%=
*100%= 
 *100%=
*100%= 














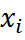 -значение осредненного признака
-значение осредненного признака -количество ед. в совокупности
-количество ед. в совокупности -показатель степени средний
-показатель степени средний
 =
= 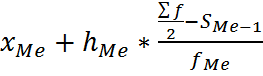
 -нижняя граница медианного интервала
-нижняя граница медианного интервала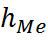 -его величина(шаг)
-его величина(шаг) -есть полусумма частот
-есть полусумма частот -накопленная частота,предшествующая медианному интервалу
-накопленная частота,предшествующая медианному интервалу -число наблюдений в медианном интервале(частота медианного интервала)
-число наблюдений в медианном интервале(частота медианного интервала)
 -нижняя граница модального интервала
-нижняя граница модального интервала -его величина(шаг)
-его величина(шаг) -частота модального интервала
-частота модального интервала -частота интервала предшествующая модальному
-частота интервала предшествующая модальному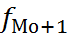 -частота интервала следующего за модальным
-частота интервала следующего за модальным
 невзвешенное среднее линейное отклонение
невзвешенное среднее линейное отклонение взвешенное среднее линейное отклонение
взвешенное среднее линейное отклонение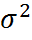 )
) ;
; 
 - среднее квадратическое отклонение
- среднее квадратическое отклонение +
+  правило сложения дисперсии
правило сложения дисперсии
 =
= 




 =
= 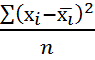
 =
=  =
= 


 =η=
=η=  =0,94(стремится к 1)
=0,94(стремится к 1) -эмпирическое корреляционное отношение
-эмпирическое корреляционное отношение =
= 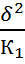 :
: 
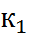 =2-1=1
=2-1=1 =N-m=5-2=3
=N-m=5-2=3 (
( )=10,13
)=10,13



 -общее среднее значение признака
-общее среднее значение признака
 - групповая дисперсия
- групповая дисперсия ).Эти показатели дают характеристику однородности,совокупности.
).Эти показатели дают характеристику однородности,совокупности. -коэф. осцилляции(изменчивости)
-коэф. осцилляции(изменчивости) - линейный коэф. вариации
- линейный коэф. вариации =
=  - коэф. Вариации
- коэф. Вариации ,то совокупность считается однородной(т.е. для распределений,близких к нормальному)
,то совокупность считается однородной(т.е. для распределений,близких к нормальному)

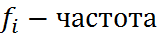



 =
= 



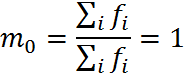

 2=
2= 

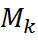 и
и  изменится вСk раз.
изменится вСk раз.  служит для вычисления коэф. ассиметрии. Если распределение ассиметрично, то M3=0, М4 служит для вычисления показателя экцесса. m1,m2,m3,m4-используют для упрощенного вычисления центральных моментов.
служит для вычисления коэф. ассиметрии. Если распределение ассиметрично, то M3=0, М4 служит для вычисления показателя экцесса. m1,m2,m3,m4-используют для упрощенного вычисления центральных моментов.
 ; а=
; а=  0 𝜎=
0 𝜎= 


 0, то спуск пологий слева
0, то спуск пологий слева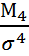 -3 интерпретируется как крутизна или островершинность распределения.
-3 интерпретируется как крутизна или островершинность распределения.



