Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды отбора единиц в выборочную совокупность.Содержание книги
Поиск на нашем сайте
1.Случайный отбор. Принцип случайного отбора состоит в том что единицы наблюдения отбираются из всей сов-ти.Случайный отбор может быть повторным и безповторным. Безповторным называется такой отбор когда отобраная единица не возвращается обратно в генир. сов-ть.(когда возвращается-то повторный отбор). 2.Механический отбор. При механ. Отборе так же применяется принцип случайного отбора,но при этом из генир. сов-ти отбирается определённое число единиц через определённый интервал. При таком способе отбора генир. сов-ть механически разбивают на равные группы, число которых равно численности выбор-й сов-ти. Приминяется мех-ий отбор при контроле качества различных продуктов. 3.Типический отбор(выборка) Еще точнее данные выбор-о наблюд-я будут если всю сов-ть разбить предварительно на отдельные типические группы,по какому-либо признаку. 4.Серийная выборка(гнездовая). Иногда в практике выбор-е наблюдения производят отбор целых групп единиц(гнезда)и внутри отобранных групп подвергают наблюдению все единицы без исключений(т.е организуют отбор и изучение нескольких серий единиц).
6 Ошибки выборочного наблюдения, примеры. Между характеристиками выборочной совокупности и искомми хар-ми генеральной совокупности сущ. Некоторые расх котор. Назыв ОШИБКОЙ ВЫБОРКИ. Теоремы: 1)неравенство Чебышева Вероятность того,что откл ген. Средней от выборочной средн. Р мало При неограниченном увеличении числа незав. Наблюд. Числа ген. Совокупности( 2) ляпунова При достаточно большом числе независимых наблюдений в гениральной совокупности с ограниченной дисперсией и конечной средней
t-коэф доверия(табл) м-средняя ошибка выборки Теорема1+Теорема2=ЗБЧ-суш. Закона больших чисел,чем обльше будет взято 1 под наблюдение тем точнее средн. Выборочное,будет воспроизводить средн.генеральную. Различ среднюю и предельную ошибки выборки связанны по формуле. Предельные ошибки выборки вычисляються по формуле.
После выисл. Находят доверит. Интервалы для ген показателе
Диспкрсия доли нах по формуле: Замечание: ормулы приведенные выше используються при определении ошибок выборки и Х генеральной совокупности осущ. Собств случ или механич отбором. 1. В случае с механич выборкой показатели вариации явяються средняя из внутри групповх дисперсий 2. При сирийной выборке показатель вариации являеться межгрупповая дисперсия Для типическиой выборки пред.ошибки вычисляються след. Образом: 1) Пр отборе пропорц. Объему типических групп
2) при отборе пропрор. Вариации приз.(не пропорционально объему типических групп)
При сирийной выборке:
7. Определение численности выборки, примеры. Разрабатывая программу выборочного изменения задают величину и довертельную веоятность
При определении численности типических групп
Замечание: величины t и ∆ задаються самим иследователем и зависят от цели иследования Параметром 1) берут из предыдущих иследований той же совокупности или определяют по результатам пробного по правилу «3-х сигм». 2) При изучении альтернатиных признаков если нет даже приблизительных следований о доле единиц оладающих заданных значений признака, берут max возм. Показать дисперсию т.е. р=0,5 3) р(1-р)=0,25
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.29 (0.006 с.) |

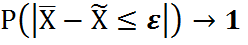 n
n 
 ) с огранич дисперсией, свероятностью сколько угодно близкой к 1 можно определить,что оклонение генеральной средней от выборочной будет скольк.угодно мало
) с огранич дисперсией, свероятностью сколько угодно близкой к 1 можно определить,что оклонение генеральной средней от выборочной будет скольк.угодно мало 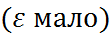







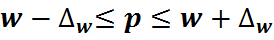


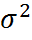
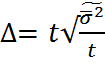 – для повторного отбора
– для повторного отбора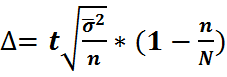 –для бесповторного отбора
–для бесповторного отбора -повторный отбор
-повторный отбор -БЕСПОВТОРНЫЙ ОТБОР
-БЕСПОВТОРНЫЙ ОТБОР –при повторнои отборе
–при повторнои отборе R и r-число средней в генеральной выборке сов.
R и r-число средней в генеральной выборке сов.
 -сирийный средний
-сирийный средний