
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое выравнивание ряда динамики.Содержание книги
Поиск на нашем сайте Метод аналитического выравнивания предполагает нахождение аналит., графической зависимости законом измен-я уровня ряда динамики во времени.
В качестве основных зависим-й выбираем: 1) Линейная зависимость. 2) Параболическая зависимость:
∑t=0; ∑
Выравнивание вариационных рядов. Закон распределения Пуассона. (1) - Основной задачей анализа вариационных рядов является изучение законов распределения и выявление характера зависимости. В ходе анализа выдвигают гипотезу о близости рассматриваемого фактического распределения к 1-му из хорошо известных типов теоретических распределений. Под теоретическим распределением понимается графическая кривая, а также распределение в чистом.виде, где накл-ся влияние случайных факторов. Чаще всего исполняют нормал. распред., распред.Пуассона. Нормальное распределение.
е, П – математическая постоянная. (σ) – сред.квадр. отклонение.
Свойства кривой нормального распределения.
1) φ (-t)= φ (t)- функция четная. 2) φ (0)= 3) S=1. 4) t=> 5) Можно найти точки перегиба 6) φ (t)= φ (t) – табул.значения. При выравнивании вариационных рядов по кривой нормального распределения теоретические частоты вычисляются: 1) N – общее число единиц. 2) Сравниваем полученные теоритические частоты с дан. убеждаемся, что их расхождения не велики, но это сопоставление графика эмпирических данных частот с теоритическими позволяет оценить эти расхождения субъективно, объективно с помощью критерия Согласия. (2) – В ряде случаев, если вариационный ряд представляет собой распредел-е по дискретному признаку, т.е. где по мере увеличения значений признака
То такой ряд можно выровнять по кривой Пуассона. При выравнивании ряда по закону Пуассона теорем.частоты определяется по формуле: 1) 2) Полученные теоретические частоты и данные фактические необходимо уравнять между собой и проверить, есть ли между ними различия, и если они есть, то случайные ли они или существ.? Таким образом проверяется гипотеза о характере распределения с помощью критерия Согласия.
Динамические ряды и их виды. Пример Определение: Рядом динамики наз-ся последова-ть значений статистического показателя признака, упорядоченная в хронологическом порядке, т.е. в порядке возрастания временного параметра. Отдельные наблюдения врем-го ряда наз-ся уровне ряда Средние характеристики ряда динамики. Пример Для обобщения данных рядов динамики рассчитывается: 1)
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.7.187 (0.006 с.) |

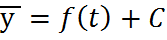 (дальше будут все у от t).
(дальше будут все у от t).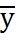 =
= 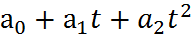 . 3)Экспоненциальная зависимость
. 3)Экспоненциальная зависимость 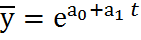 ;
; 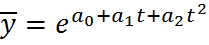 . Рассмотрим линейную зависимость: 1) а0;а1 находится из (*). 2) а0, а1, а2 =?(для параболической зависимости). Найдём их, исполняя метод наим. кв.в.:
. Рассмотрим линейную зависимость: 1) а0;а1 находится из (*). 2) а0, а1, а2 =?(для параболической зависимости). Найдём их, исполняя метод наим. кв.в.:  => min.
=> min. =>
=> 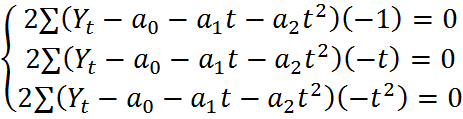 /:2
/:2 
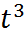 =0.
=0. 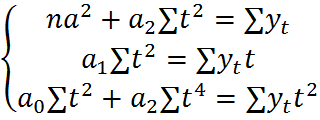

 =
=  ;
; 

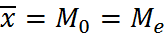
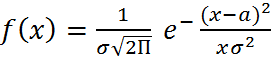 – плотность распределения вероятности.
– плотность распределения вероятности.  =t – стандартизац-е отклонение(нормированное).
=t – стандартизац-е отклонение(нормированное). ;
;  ;
;  .
.
 - дисперсия
- дисперсия – сред. арифм.(сред.величины).
– сред. арифм.(сред.величины).
 =
=  ;
; ; φ (t)=>0;
; φ (t)=>0; 0.
0. 2)
2)  .
. (частот); h – длина интервалов в группах. (σ) – сред.квадратич.отклон-е.
(частот); h – длина интервалов в группах. (σ) – сред.квадратич.отклон-е. (получен.).
(получен.). частоты резко уменьшаются, где
частоты резко уменьшаются, где  .
.
 .
.  – вероятность наступления отдельных значений
– вероятность наступления отдельных значений 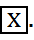

 N- общее число единиц ряда.
N- общее число единиц ряда. . Каждый ряд динамики содержит два элемента: 1)Значение времени; 2)Значение уровня ряда. В зависимости от хар-ра временного параметра ряды делятся на моментные и интервальные. В моментных рядах динамики уровни характеризуют значение показателей по состоянию на определенные моменты времени(даты). Например, ряды цен на определенные уровни товаров. Ряды курсов акций, уровни которых фиксируются в конкретных числах. Ряды численности мужского и женского населения, ряды стоимости основных производственных фондов. Т.к. значение уровней этих рядов опреде-ся ежегодно на одно и тоже число. В интервальных рядах уровни характер-ся значениями показателя за определенные интервалы. Например, ряды годовой, месячной, квартальной, динамики производства продукции в натуральном или стоимостном выражении. Уровне рядов динамики могут представлять собой абсолютные, относительные и средние величины. В таком случае ряды наз-ся производными. Правило построения рядов динамики: 1)необходимо соблюдать периодичность развития явления.2)величины временных интервалов должны соответствовать интенсивности изменения изучаемого объекта.3)числовые уровни рядов динамики должны быть упорядочены во времени, не допускается анализ рядов динамики с пропуском во времени.
. Каждый ряд динамики содержит два элемента: 1)Значение времени; 2)Значение уровня ряда. В зависимости от хар-ра временного параметра ряды делятся на моментные и интервальные. В моментных рядах динамики уровни характеризуют значение показателей по состоянию на определенные моменты времени(даты). Например, ряды цен на определенные уровни товаров. Ряды курсов акций, уровни которых фиксируются в конкретных числах. Ряды численности мужского и женского населения, ряды стоимости основных производственных фондов. Т.к. значение уровней этих рядов опреде-ся ежегодно на одно и тоже число. В интервальных рядах уровни характер-ся значениями показателя за определенные интервалы. Например, ряды годовой, месячной, квартальной, динамики производства продукции в натуральном или стоимостном выражении. Уровне рядов динамики могут представлять собой абсолютные, относительные и средние величины. В таком случае ряды наз-ся производными. Правило построения рядов динамики: 1)необходимо соблюдать периодичность развития явления.2)величины временных интервалов должны соответствовать интенсивности изменения изучаемого объекта.3)числовые уровни рядов динамики должны быть упорядочены во времени, не допускается анализ рядов динамики с пропуском во времени. средний уровень ряда; 2)
средний уровень ряда; 2)  ,
,  средние темпы роста и прироста;3)
средние темпы роста и прироста;3)  средний абсолютный прирост. Определение: Средний уровень ряда это показатель обобщающий итоги разбития явления за единичный интервал или момент из имеющейся временной последовательности. 1. Интервальный ряд: а) с равным промежутком времени
средний абсолютный прирост. Определение: Средний уровень ряда это показатель обобщающий итоги разбития явления за единичный интервал или момент из имеющейся временной последовательности. 1. Интервальный ряд: а) с равным промежутком времени  ,где n-общая длина временного ряда или общее число равных временных отрезков. б) с неравными периодами времени
,где n-общая длина временного ряда или общее число равных временных отрезков. б) с неравными периодами времени  где
где  -продолжительность периода. 2.Моментные ряды: а) с равными периодами времени t
-продолжительность периода. 2.Моментные ряды: а) с равными периодами времени t  - хронологическая средняя. б)с неравными периодами времени
- хронологическая средняя. б)с неравными периодами времени 
 ,
,  . Рассмотрим фор-лы для среднего абсолютного прироста:
. Рассмотрим фор-лы для среднего абсолютного прироста:  =
=  =
=  .
.  =
=  =
=  , m=n-1, где n-кол-во периодов, m-число коэф-ов роста.
, m=n-1, где n-кол-во периодов, m-число коэф-ов роста. 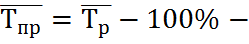 средний темп роста.
средний темп роста.


