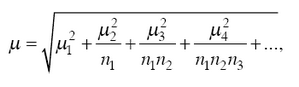Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочный метод в статистических исследованияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выборочный метод статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку. Математическая теория В. м. опирается на два важных раздела математической статистики (См. Математическая статистика) — теорию выбора из конечной совокупности и теорию выбора из бесконечной совокупности. Основное отличие В. м. для конечной и бесконечной совокупностей заключается в том, что в первом случае В. м. применяется, как правило, к объектам неслучайной, детерминированной природы (например, число дефектных изделий в данной партии готовой продукции не является случайной величиной (См. Случайная величина): это число — неизвестная постоянная, которую и надлежит оценить по выборочным данным). Во втором случае В. м. обычно применяется для изучения свойств случайных объектов (например, для исследования свойств непрерывно распределённых случайных ошибок измерений, каждое из которых теоретически может быть истолковано как реализация одного из бесконечного множества возможных результатов). Выбор из конечной совокупности и его теория являются основой статистических методов контроля качества и часто применяются в социологических исследованиях (см. Выборочное наблюдение). Согласно теории вероятностей, выборка будет правильно отражать свойства всей совокупности, если выбор производится случайно, т. е. так, что любая из возможных выборок заданного объёма n из совокупности объёма N [число таких выборок равно N!/n!(N — n)!] имеет одинаковую вероятность быть фактически выбранной. На практике наиболее часто используется выбор без возвращения (бесповторная выборка), когда каждый отобранный объект перед выбором следующего объекта в исследуемую совокупность не возвращается (такой выбор применяется при статистическом контроле качества). Выбор с возвращением (выборка с повторением) рассматривается обычно лишь в теоретических исследованиях (примером выбора с возвращением является регистрация числа частиц, коснувшихся в течение данного времени стенок сосуда, внутри которого совершается Броуновское движение). Если n << N, то повторный и бесповторный выборы дают практически эквивалентные результаты. Свойства совокупности, исследуемые В. м., могут быть качественными и количественными. В первом случае задача выборочного обследования заключается в определении количества М объектов совокупности, обладающих каким-либо признаком (например, при статистическом контроле часто интересуются количеством М дефектных изделий в партии объёма N). Оценкой для М служит отношение μN/n, где μ — число объектов с данным признаком в выборке объёма n. В случае количественного признака имеют дело с определением среднего значения совокупности В математической теории В. м. оценка средних значений занимает центральное место потому, что к ней в известной степени сводится изучение изменчивости признака внутри совокупности, так как за характеристику изменчивости обычно принимают дисперсию
представляющую собой среднее значение квадратов отклонений xi от их среднего значения 2 = М (N — M)/N2. О точности оценок μ/n и ξ̅ судят по их дисперсиям
которые в терминах дисперсии конечной совокупности σ2 выражаются в виде отношений σ2/n (в случае выборок с повторением) и σ2(N — n)/n (N — 1) (в случае бесповторных выборок). Так как во многих практически интересных задачах случайные величины μ/n и ξ̅ при n ≥ 30 приближённо подчиняются нормальному распределению, то отклонения μ/n от M/N и ξ̅ от x̅, превышающие по абсолютной величине 2σμ/n и Выбор из бесконечной совокупности. В математической статистике результаты каких-либо однородных наблюдений (чаще всего независимых) принято называть выборкой даже в том случае, когда эти результаты не соответствуют понятию выборки с повторениями или без повторений из конечной совокупности. Например, результаты измерений углов на местности, подверженные независимым непрерывно распределённым случайным ошибкам, часто называют выборкой из бесконечной совокупности. Предполагается, что принципиально можно осуществить любое число таких наблюдений. Полученные фактически результаты считают выборкой из бесконечного множества возможных результатов, называемых генеральной совокупностью. Понятие генеральной совокупности не является логически безупречным и необходимым. Для решения практических задач нужна не сама бесконечная генеральная совокупность, а лишь те или иные характеристики, которые ей ставятся в соответствие. Эти характеристики с точки зрения теории вероятностей являются числовыми или функциональными характеристиками некоторого распределения вероятностей, а элементы выборки —случайными величинами, подчиняющимися этому распределению. Такое истолкование позволяет распространить на выборочные оценки общую теорию статистических оценок. По этой причине, например, в вероятностной теории обработки наблюдений понятие бесконечной генеральной совокупности заменяется понятием распределения вероятностей, содержащего неизвестные параметры. Результаты наблюдений истолковываются как экспериментально наблюдаемые значения случайных величин, подчиняющихся этому распределению, Цель обработки — вычисление по результатам наблюдений в том или ином смысле оптимальных статистических оценок для неизвестных параметров распределения. Смысл случайных ошибок ОШИБОК ТЕОРИЯ - раздел математич. статистики, посвященный построению уточненных выводов о численных значениях приближенно измеренных, величин, а также об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, т. <к. каждое измерение содержит нек-рую ошибку. Различают три основных вида ошибок: систематические, грубые и случайные. Систематические ошибки все время либо преувеличивают, либо преуменьшают результаты измерений и происходят от определенных причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на измерения и изменяющих их в одном направлении. Оценка систематич. ошибок производится с помощью методов, выходящих за пределы математич. статистики (см. Наблюдений обработка). Грубые ошибки возникают в результате просчета, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредвиденным образом то в сторону уменьшения, то в сторону увеличения результатов. О. т. занимается изучением лишь грубых и случайных ошибок. Основные задачи О. т.: разыскание законов распределения случайных ошибок, разыскание оценок (см. Оценка статистическая).неизвестных измеряемых величин по результатам измерений, установление погрешностей таких оценок и установление грубых ошибок. Пусть в результате пнезависимых равноточных измерений нек-рой неизвестной величины m, получены значения Y1, Y2,..., Yn. Разности
наз. истинными ошибками. В терминах вероятностной О. т. все di трактуются как случайные величины; независимость измерений понимается как взаимная независимость случайных величин d1,..., dn. Равноточность измерений в широком смысле истолковывается как одинаковая распределенность: истинные ошибки равноточных измерений суть одинаково распределенные случайные величины. При этом математич. ожидание истинных ошибок
а разности
наз. кажущимися ошибками. Выбор
Опыт показывает, что практически очень часто случайные ошибки di подчиняются распределениям, близким к нормальному (причины этого вскрыты т. н. предельными теоремами теории вероятностей). В этом случае величина Если дисперсия s2 отдельных измерений заранее неизвестна, то для ее оценки пользуются величиной
(
подчиняется Стъюдента распределению с п-1 степенями свободы. Этим можно воспользоваться для оценки погрешности приближенного равенства Величина (п-1)s2/s2 при тех же предположениях имеет "хи-квадрагп" распределение с n-1 степенями свободы. Это позволяет оценить погрешность приближенного равенства
где F(z, п-1) - функция c2 –распределения
Если нек-рые измерения содержат грубые ошибки, то предыдущие правила оценки m и s дадут искаженные результаты. Поэтому очень важно уметь отличать измерения, содержащие грубые ошибки, от измерений, подверженных лишь случайным ошибкам di. Для случая, когда di независимы и имеют одинаковое нормальное распределение, наиболее совершенный способ выявления измерений, содержащих грубые ошибки, предложен Н. В. Смирновым.
Билет 41 - Виды выборок В теории выборочного метода разработаны различные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора. В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки: · собственно случайную; · механическую; · типическую (стратифицированную, районированную); · серийную (гнездовую); · комбинированную; · многоступенчатую; · многофазную; · взаимопроникающую. Собственно случайная выборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц. Случайный порядок подобен жеребьевке. На практике он чаще всего применяется при использовании специальных таблиц случайных чисел. Если, например, из совокупности, содержащей 1587 единиц, следует отобрать 40 единиц, то из таблицы отбирают 40 четырехзначных чисел, которые меньше 1587. В том случае, когда собственно случайная выборка организуется как повторная, расчет стандартной ошибки производится в соответствии с формулой (6.1). При бесповторном способе отбора формула для расчета стандартной ошибки будет:
где 1 – n / N – доля единиц генеральной совокупности, не попавших в выборку. Так как эта доля всегда меньше единицы, то ошибка при бесповторном отборе при прочих равных условиях всегда меньше, чем при повторном. Бесповторный отбор организовать легче, чем повторный, и он применяется намного чаще. Однако величину стандартной ошибки при бесповторном отборе можно определять по более простой формуле (5.1). Такая замена возможна, если доля единиц генеральной совокупности, не попавших в выборку, большая и, следовательно, величина близка к единице. Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно, а иногда невозможно, так как при использовании таблиц случайных чисел необходимо пронумеровать все единицы генеральной совокупности. Довольно часто генеральная совокупность такая большая, что провести подобную предварительную работу чрезвычайно сложно и нецелесообразно, поэтому на практике применяют другие виды выборок, каждая из которых не является строго случайной. Однако организуются они так, чтобы было обеспечено максимальное приближение к условиям случайного отбора. При чисто механической выборке вся генеральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, составленного в каком-то нейтральном по отношению к изучаемому признаку порядке, например по алфавиту. Затем список единиц отбора разбивается на столько равных частей, сколько необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отбирается одна единица. Этот вид выборки не всегда может обеспечить случайный характер отбора, и полученная выборка может оказаться смещенной. Объясняется это тем, что, во-первых, упорядочение единиц генеральной совокупности может иметь элемент неслучайного характера. Во-вторых, отбор из каждой части генеральной совокупности при неправильном установлении начала отсчета может также привести к ошибке смещения. Однако практически легче организовать механическую выборку, чем собственно случайную, и при проведении выборочных обследований чаще всего пользуются этим видом выборки. Стандартную ошибку при механической выборке определяют по формуле собственно случайной бесповторной выборки (6.2). Типическая (районированная, стратифицированная) выборка преследует две цели: • обеспечить представительство в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам; • увеличить точность результатов выборочного обследования. При типической выборке до начала ее формирования генеральная совокупность единиц разбивается на типические группы. При этом очень важным моментом является правильный выбор группировочного признака. Выделенные типические группы могут содержать одинаковое или различное число единиц отбора. В первом случае выборочная совокупность формируется с одинаковой долей отбора из каждой группы, во втором – с долей, пропорциональной ее доле в генеральной совокупности. Если выборка формируется с равной долей отбора, по существу она равносильна ряду собственно случайных выборок из меньших генеральных совокупностей, каждая из которых и есть типическая группа. Отбор из каждой группы осуществляется в случайном (повторном или бесповторном) либо механическом порядке. При типической выборке, как с равной, так и неравной долей отбора, удается устранить влияние межгрупповой вариации изучаемого признака на точность ее результатов, так как обеспечивается обязательное представительство в выборочной совокупности каждой из типических групп. Стандартная ошибка выборки будет зависеть не от величины общей дисперсии?2, а от величины средней из групповых дисперсий?i2. Поскольку средняя из групповых дисперсий всегда меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической выборки будет меньше стандартной ошибки собственно случайной выборки. При определении стандартных ошибок типической выборки применяются следующие формулы: • при повторном способе отбора:
• при бесповторном способе отбора:
– средняя из групповых дисперсий в выборочной совокупности. Серийная (гнездовая) выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Серийную выборку практически организовать и провести легче, чем отбор отдельных единиц. Однако при этом виде выборки, во-первых, не обеспечивается представительство каждой из серий и, во-вторых, не устраняется влияние межсерийной вариации изучаемого признака на результаты обследования. В том случае, когда эта вариация значительна, она приведет к увеличению случайной ошибки репрезентативности. При выборе вида выборки исследователю необходимо учитывать это обстоятельство. Стандартная ошибка серийной выборки определяется по формулам: • при повторном способе отбора:
• при бесповторном способе отбора:
В практике те или иные способы и виды выборок применяются в зависимости от цели и задач выборочных обследований, а также возможностей их организации и проведения. Чаще всего применяется комбинирование способов отбора и видов выборки. Такие выборки получили название комбинированные. Комбинирование возможно в разных сочетаниях: механической и серийной выборки, типической и механической, серийной и собственно случайной и т. д. К комбинированной выборке прибегают для обеспечения наибольшей репрезентативности с наименьшими трудовыми и денежными затратами на организацию и проведение обследования. При комбинированной выборке величина стандартной ошибки выборки состоит из ошибок на каждой ее ступени и может быть определена как корень квадратный из суммы квадратов ошибок соответствующих выборок. Так, если при комбинированной выборке в сочетании использовались механическая и типическая выборки, то стандартную ошибку можно определить по формуле
Особенность многоступенчатой выборки состоит в том, что выборочная совокупность формируется постепенно, по ступеням отбора. На первой ступени с помощью заранее определенного способа и вида отбора отбираются единицы первой ступени. На второй ступени из каждой единицы первой ступени, попавшей в выборку, отбираются единицы второй ступени и т. д. Число ступеней может быть и больше двух. На последней ступени формируется выборочная совокупность, единицы которой подлежат обследованию. Так, например, для выборочного обследования бюджетов домашних хозяйств на первой ступени отбираются территориальные субъекты страны, на второй – районы в отобранных регионах, на третьей – в каждом муниципальном образовании отбираются предприятия или организации и, наконец, на четвертой ступени – в отобранных предприятиях отбираются семьи. Таким образом, выборочная совокупность формируется на последней ступени. Многоступенчатая выборка более гибкая, чем другие виды, хотя в общем она дает менее точные результаты, чем выборка того же объема, но сформированная в одну ступень. Однако при этом она имеет одно важное преимущество, которое заключается в том, что основу выборки при многоступенчатом отборе нужно строить на каждой из ступеней только для тех единиц, которые попали в выборку, а это очень важно, так как нередко готовой основы выборки нет. Стандартную ошибку выборки при многоступенчатом отборе при группах разных объемов определяют по формуле
где?1,?2,?3,... – стандартные ошибки на разных ступенях; n1, n2, n3,... – численность выборок на соответствующих ступенях отбора. В том случае, если группы неодинаковы по объему, то теоретически этой формулой пользоваться нельзя. Но если общая доля отбора на всех ступенях постоянна, то практически расчет по этой формуле не приведет к искажению величины ошибки. Сущность многофазной выборки состоит в том, что на основе первоначально сформированной выборочной совокупности образуют подвыборку, из этой подвыборки – следующую подвыборку и т. д. Первоначальная выборочная совокупность представляет собой первую фазу, подвыборка из нее – вторую и т. д. Многофазную выборку целесообразно применять в случаях, если: · для изучения различных признаков требуется неодинаковый объем выборки; · колеблемость изучаемых признаков неодинакова и требуемая точность различна; · в отношении всех единиц первоначальной выборочной совокупности (первая фаза) необходимо собрать менее подробные сведения, а в отношении единиц каждой последующей фазы – более подробные.
Одним из несомненных достоинств многофазной выборки является то обстоятельство, что сведениями, полученными на первой фазе, можно пользоваться как дополнительной информацией на последующих фазах, информацией второй фазы – как дополнительной информацией на следующих фазах и т. д. Такое использование сведений повышает точность результатов выборочного обследования. При организации многофазной выборки можно применять сочетание различных способов и видов отбора (типическую выборку с механической и т. д.). Многофазный отбор можно сочетать с многоступенчатым. На каждой ступени выборка может быть многофазной. Стандартная ошибка при многофазной выборке рассчитывается на каждой фазе в отдельности в соответствии с формулами того способа отбора и вида выборки, при помощи которых формировалась ее выборочная совокупность. Взаимопроникающие выборки – это две или более независимые выборки из одной и той же генеральной совокупности, образованные одним и тем же способом и видом. К взаимопроникающим выборкам целесообразно прибегать, если необходимо за короткий срок получить предварительные итоги выборочных обследований. Взаимопроникающие выборки эффективны для оценки результатов обследования. Если в независимых выборках результаты одинаковы, то это свидетельствует о надежности данных выборочного обследования. Взаимопроникающие выборки иногда можно применять для проверки работы различных исследователей, поручив каждому из них провести обследование разных выборок. Стандартная ошибка при взаимопроникающих выборках определяется по той же формуле, что и типическая пропорциональная выборка (5.3). Взаимопроникающие выборки по сравнению с другими видами требуют больших трудовых затрат и денежных расходов, поэтому исследователь должен учитывать это обстоятельство при проектировании выборочного обследования. Предельные ошибки при различных способах отбора и видах выборки определяются по формуле? = t?, где? – соответствующая стандартная ошибка.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.250 (0.01 с.) |

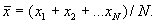 является выборочное среднее
является выборочное среднее  1,..., ξn — те значения из исследуемой совокупности x1, x2,..., xN, которые принадлежат выборке. С математической точки зрения 1-й случай — частная разновидность 2-го, которая имеет место, когда М величин xi равны 1, а остальные (N — М) равны 0; в этой ситуации
1,..., ξn — те значения из исследуемой совокупности x1, x2,..., xN, которые принадлежат выборке. С математической точки зрения 1-й случай — частная разновидность 2-го, которая имеет место, когда М величин xi равны 1, а остальные (N — М) равны 0; в этой ситуации

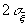 n ≥ 30 осуществиться в среднем приблизительно в одном случае из двадцати. Более полную информацию о распределении количественного признака в данной совокупности можно получить с помощью эмпирического Распределения этого признака в выборке.
n ≥ 30 осуществиться в среднем приблизительно в одном случае из двадцати. Более полную информацию о распределении количественного признака в данной совокупности можно получить с помощью эмпирического Распределения этого признака в выборке.
 аз. систематической ошибкой, а разности d1-b,...,dn-b - случайными ошибками. Таким образом, отсутствие систематич. ошибки означает, что b=0 и в этой ситуации d1,..., dn суть случайные ошибки. Величину
аз. систематической ошибкой, а разности d1-b,...,dn-b - случайными ошибками. Таким образом, отсутствие систематич. ошибки означает, что b=0 и в этой ситуации d1,..., dn суть случайные ошибки. Величину  , где s - квадратичное отклонение, наз. мерой точности (при наличии систематич. ошибки мера точности выражается отношением
, где s - квадратичное отклонение, наз. мерой точности (при наличии систематич. ошибки мера точности выражается отношением  . Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерении. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для нек-рых отдельных измерений. В качестве оценки неизвестной величины и обычно берут арифметич. среднее из результатов измерений
. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерении. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для нек-рых отдельных измерений. В качестве оценки неизвестной величины и обычно берут арифметич. среднее из результатов измерений

 в качестве оценки для m основан на том, что при достаточно большом числе га равноточных измерений, лишенных систематич. ошибки, оценки
в качестве оценки для m основан на том, что при достаточно большом числе га равноточных измерений, лишенных систематич. ошибки, оценки 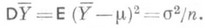
 . Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
. Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
 , то есть s2- несмещенная оценка для s2). Если случайные ошибки di имеют нормальное распределение, то отношение
, то есть s2- несмещенная оценка для s2). Если случайные ошибки di имеют нормальное распределение, то отношение

 . Можно показать, что относительная погрешность не будет превышать числа qс вероятностью
. Можно показать, что относительная погрешность не будет превышать числа qс вероятностью




 где?– межсерийная дисперсия выборочной совокупности; r – число отобранных серий;
где?– межсерийная дисперсия выборочной совокупности; r – число отобранных серий; где R – число серий в генеральной совокупности.
где R – число серий в генеральной совокупности. где?1 и?2 – стандартные ошибки соответственно механической и типической выборок.
где?1 и?2 – стандартные ошибки соответственно механической и типической выборок.