Билет 43 – Дисперсионный анализ

Дисперсионный анализ – анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов.

Обобщенно задача дисперсионного анализа состоит в том, чтобы из общей вариативности признака выделить три частные вариативности:

- Вариативность, обусловленную действием каждой из исследуемых независимых переменных.

- Вариативность, обусловленную взаимодействием исследуемых независмых переменных.

- Вариативность случайную, обусловленную всеми неучтенными обстоятельствами.

Вариативность, обусловленная действием исследуемых переменных и их взаимодействием соотносится со случайной вариативностью. Показателем этого соотношения является F – критерий Фишера (метод, не имеющий ничего общего, кроме автора, с «угловым преобразованием Фишера»).

FэмпА = Вариативность, обусловленная действием переменной А / Случайная вариативность

FэмпБ = Вариативность, обусловленная действием переменной Б / Случайная вариативность

FэмпАБ = Вариативность, обусловленная взаимодействием А и Б / Случайная вариативность

В формулу расчета критерия F взодят оценки дисперсий, и, следовательно, этот метод относится к разряду параметрических. Чем в большей степени вариативность признака обусловлена исследуемыми переменными или их взаимодействием, тем выше эмпирические значения критерия F.

В отличие от корреляционного анализа, в дисперсионном исследователь исходит из предположения, что одни переменные выступают как влияющие (именуемые факторами или независимыми переменными), а другие (результативные признаки или зависимые переменные) – подвержены влиянию этих факторов. Хотя такое допущение и лежит в основе математических процедур расчета, оно, однако, требует осторожности рассуждений об источнике и объекте влияния.

Представим смысл дисперсионного анализа графически

Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F—критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов.

Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок: x₁,…,x_n которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).

Виды дисперсионного анализа

Дисперсионный анализ схематически можно подразделить на несколько категорий. Это деление осуществляется, смотря по тому, сколько, во-первых, факторов принимает участие в рассмотрении, во-вторых, - сколько переменных подвержены действию факторов, и, в-третьих, - по тому, как соотносятся друг с другом выборки значений.

При наличии одного фактора, влияние которого исследуется, дисперсионный анализ именуется однофакторным, и распадается на две разновидности:

 

- Анализ несвязанных (то есть – различных) выборок. Например, одна группа респондентов решает задачу в условиях тишины, вторая – в шумной комнате. (В этом случае, к слову, нулевая гипотеза звучала бы так: «среднее время решения задач такого-то типа будет одинаково в тишине и в шумном помещении», то есть не зависит от фактора шума.)

- Анализ связанных выборок. То есть: двух замеров, проведенных на одной и той же группе респондентов в разных условиях. Тот же пример: в первый раз задача решалась в тишине, второй – сходная задача – в условиях шумовых помех. (На практике к подобным опытам следует подходить с осторожностью, поскольку в действие может вступить неучтенный фактор «научаемость», влияние которого исследователь рискует приписать изменению условий, а именно, - шуму.)

В случае, если исследуется одновременное воздействие двух или более факторов, мы имеем дело с многофакторным дисперсионным анализом, который также можно подразделить по типу выборки.

Если же воздействию факторов подвержено несколько переменных, - речь идет о многомерном анализе.

Ограничения дисперсионного анализа и подготовка данных

Дисперсионный анализ следует применять тогда, когда известно (установлено), что распределение результативного признака является нормальным.

Для проверки следует провести расчеты ассимметрии и эксцесса по следующим формулам:

A = Σ (x_i – x_ср)³ / ns³

m_A= √(6/n)

E = (Σ (x_i – x_ср)⁴ / ns⁴) - 3

m_E= 2√(6/n)

где А и Е – ассимметрия и эксцесс, а mA и mE – их ошибки репрезентативности. После подстановки значений не должно оказаться так, чтобы ассимметрия и эксцесс превышали более, чем втрое свои ошибки репрезентативности. При соблюдении этого требования, распределение можно считать нормальным.

Будем называть данные, относящиеся к одному условию действия фактора (к одной градации) дисперсионным комплексом.

Дисперсионный анализ требует также, чтобы между комплексами соблюдалось равенство дисперсий. В литературе по этому вопросу предлагается (и доказана правомочность предложения) удовлетворять такое требование уравниванием числа значений в каждом из комплексов. Иными словами, если в тихой аудитории решали задачу 10 человек, то и в шумную мы должны посадить столько же; если белых кур набралось 100, черных – 80, а пестрых – 70, - мы обязаны взять только по 70 кур каждого цвета. Причем, отбор следует осуществлять случайным образом.

Однофакторный дисперсионный анализ для несвязанных выборок

Назначение метода

Метод однофакторного дисперсионного анализа применяется в тех случаях, когда исследуются изменения результативного признака (зависимой переменной) под влиянием изменяющихся условий или градаций какого-либо фактора.

Влиянию каждой из градаций фактора подвержены разные выборки.

Должно быть не менее трех градаций фактора и не менее двух наблюдений в каждой градации.

Описание метода

Расчеты начинаются с расстановки всех данных по столбцам, относящимся к каждому из факторов соответственно.

Следующим действием будет нахождение сумм значений по столбцам (то есть – градациям) и возведение их в квадрат.

Фактически метод состоит в сопоставлении каждой из полученных и возведенных в квадрат сумм с суммой квадратов всех значений, полученных во всем эксперименте.

Графическое представление метода

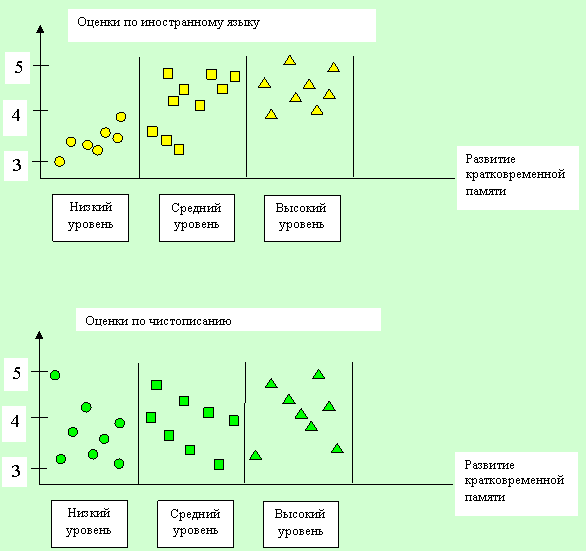
На рисунке схематически представлены три градации какого-либо фактора. Дисперсионный анализ позволяет определить, что преобладает: влияние фактора или случайная вариативность внутри групп (тенденция, выраженная кривой или размах отрезков, ограниченных кружками)?

Однофакторный дисперсионный анализ для связанных выборок

Назначение метода

Метод применяется в тех случаях, когда исследуется влияние разных условий действия фактора (градаций фактора) на одну и ту же выборку. (Одни и те же респонденты в разных условиях.)

Условий (градаций) должно быть не менее трех.

Индивидуальных значений по каждому условию должно быть не менее двух.

Описание метода

В этом случае различия могут быть вызваны не только влиянием фактора, но и индивидуальными различиями между испытуемыми. При анализе несвязанных выборок это обстоятельство не оказывало воздействия за счет того, что выборки были различны, и сводилось к случайным причинам различий, - здесь же индивидуальные различия между элементами выборки (респондентами) необходимо особо учитывать. (Индивидуальные различия могут оказаться более значимыми, чем изменение условий действия фактора.) Исходя из сказанного, в расчеты вводятся дополнительные компоненты – суммы квадратов сумм индивидуальных значений.

Графическое представление

Рисунок иллюстрирует пример решения анаграмм различной длины одними и теми же респондентами. Исследователей интересовало влияние длины анаграммы на время ее решения. (Выяснилось, что наибольшие трудности, что видно из диапазона времени, затраченного на решение, и его среднего значения, вызвала анаграмма из пяти букв.)