Сравнение и анализ двух выборок

 

Для выявления различий между двумя выборками с известным законом распределения применяют t-критерий различия Стьюдента и критерий различия Фишера. При этом предполагается, что данные распределены по нормальному закону. Первый критерий сравнивает средние двух выборок и вычисляет вероятность того, что они относятся к одной и той же генеральной совокупности. Второй критерий проверяет принадлежность дисперсий двух выборок одной генеральной совокупности. В обоих случаях по вычисленной вероятности судят о принадлежности выборок к одной или разным совокупностям: если вероятность случайного появления значений в исследуемых выборках меньше уровня значимости a<0.05, то различия между выборками не случайны и они достоверно отличаются друг от друга.

Рассмотрим использование t-критерия Стьюдента для определения наличия различий между двумя выборками. При этом выборки могут быть:

- независимыми, несвязными с разным числом значений в выборках – анализируют с помощью инструмента Двухвыборочный t-тест с различными дисперсиями или Двухвыборочный t-тест с одинаковыми дисперсиями;

- зависимыми, связанными с равным числом значений в выборках – анализируют с помощью инструмента Парный двухвыборочный t-тест для средних или Двухвыборочный t-тест с различными дисперсиями.

Включенная в Excel функция ТТЕСТ для оценки отличий по t-критерия Стьюдента имеет параметр Тип для настройки на один из видов t -теста: 1 – парный тест, 2 - двухвыборочный t -тест с одинаковыми дисперсиями, 3 - двухвыборочный t -тест с разными дисперсиями.

На рис. 2.91 приведены данные о месячных продажах хлебцев Burger, продаваемых без рекламы, и хлебцев Finn Crisp, продаваемых с рекламной поддержкой. Необходимо выявить достоверность различий в этих данных. Здесь же приведены результаты функции ТТЕСТ (ячейка В14) и инструмента Двухвыборочный t-тест с различными дисперсиями.

 

Рис. 2.91

 

Полученное с помощью функции ТТЕСТ значение величины случайного появления анализируемых выборок 0.07895 больше уровня значимости a=0.05. Таким образом, различия между выборками случайны и считаются не отличающимися друг от друга, что говорит о неэффективности рекламной поддержки хлебцев Finn Crisp и, возможно, о б о льшей «раскрученности» бренда Burger. Аналогичные результаты получены инструментом Двухвыборочный t-тест с различными дисперсиями – вероятность случайного появления выборок P(T<=t) двухстороннее =0.0787.

Воспроизведите полученные результаты. В ячейку В14 введите функцию ТТЕСТ из группы Статистические, заполните параметры, как на рис. 2.92 и нажмите ОК. Здесь выбран Тип=3, поскольку выборки не связаны, независимы и с разным числом значений.

 

Рис. 2.92

 

Далее вызовите инструмент Двухвыборочный t-тест с различными дисперсиями через меню С е рвисàАна л из данных…. На рис. 2.93 показано заполнение параметров инструмента. Интервал переменной 1 $А$2:$A$10 и интервал переменной 2 $B$2:$B$12 это диапазоны анализируемых данных. Выходной интервал $D$1 – это ячейка, начиная с которой будет выведен результат. Поле Альфа позволяет установить требуемый уровень значимости a=0.05.

 

Рис. 2.93

 

Отметим важность правильного подбора типа t -теста, поскольку для одних и тех же данных они могут давать разные результаты. Если выбор типа t -теста не очевиден, то правильным будет применение двухвыборочного t -теста с разными дисперсиями как общий случай анализа; если выборки зависимы и связаны, то применяют парный t -тест.

 

 

Дисперсионный анализ

 

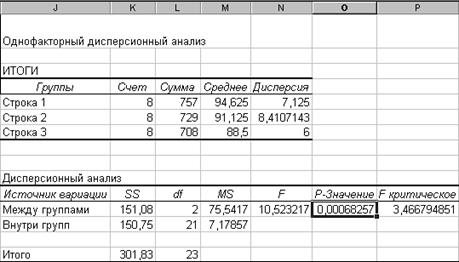
Часто требуется оценить существенность влияния на выборки одного или нескольких факторов. При этом выборки должны стремиться к нормальному распределению и быть независимыми. В Excel включены следующие инструменты: Однофакторный дисперсионный анализ, Двухфакторный дисперсионный анализ с повторениями, Двухфакторный дисперсионный анализ без повторения.

Рассмотрим однофакторный дисперсионный анализ. Степень влияния фактора на выборку определяется сравнением дисперсий двух выборок: выборки с наличием исследуемого фактора и выборки без этого фактора (со случайными причинами). Инструмент Excel Однофакторный дисперсионный анализ вычисляет вероятность случайности различий (Р-значение), которая указывает на значимость различий: если уровень значимости меньше 0.05, то различия не случайны и говорят о статистическом влиянии фактора на выборку (переменную).

В качестве примера проведем анализ влияния фактора цены комплексного обеда на дневную посещаемость кафе – рис. 2.94. На рис. 2.95 приведен результат анализа: Р-значение =0.00068257 <0.05. Это доказывает влияние фактора цены на посещаемость кафе.

 

Рис. 2.94

 

Рис. 2.95

 

Воспроизведите полученные результаты. Введите данные и вызовите инструмент Однофакторный дисперсионный анализ через меню С е рвисàАна л из данных…. На рис. 2.96 показано заполнение параметров инструмента. Входной интервал $В$2:$I$4 это диапазон исследуемых данных. Переключатель Группирование установлен по строкам, т.к. выборки располагаются по строкам. Выходной интервал $J$1 – это ячейка, начиная с которой будет выведен результат. Поле Альфа позволяет установить требуемый уровень значимости, здесь a=0.05.

 

Рис. 2.96