Построение выборочной функции распределения

 

Для построения выборочных функций распределения в Excel используют инструмент Гистограмма из Пакета анализа или функция ЧАСТОТА. При этом весь диапазон изменения случайной величины разбивают на интервалы равной ширины, называемые карманами. Число карманов обычно 5-15. Вычисляется число попаданий значений случайной величины в каждый карман. По ним вычисляются статистические (относительные) частоты - отношение числа попаданий в карман m к общему числу испытаний n (m / n), по которым и строится гистограмма выборочной функции распределения статистических вероятностей.

В качестве примера построим выборочное распределение по данным о ежедневных продажах некоторого товара – на рис. 2.76 показана выборка за 2 месяца. Здесь же заведен диапазон карманов – граничных значений. Данные будут группироваться в интервалы 0-170, 171-175, 176-180 и т.д.: при подсчете в карман включаются значения на правой (нижней) границе и не включаются значения на левой (верхней) границе.

 

Рис. 2.76

 

Построим выборочное распределение дневных продаж инструментом Гистограмма: вызов через меню С е рвисàАна л из данных….

 

Рис. 2.77

На рис. 2.77 показано заполнение параметров инструмента. Входной интервал $А$3:$Е$14 - это диапазон исследуемых данных. Интервал карманов $G$2:$G$14 - это границы, в которые группируются входные данные. Выходной интервал $I$1 – это ячейка, начиная с которой будет выведен результат. Установите также флажок Вывод графика - гистограммы. Флажок Интегральный процент устанавливают, если надо вычислить проценты частот с накоплением и вывести график интегральных процентов. Результат работы инструмента показан на рис. 2.78.

 

Рис. 2.78

 

Теперь построим выборочное распределение дневных продаж, воспользовавшись функцией ЧАСТОТА. Результат показан на рис. 2.79. Здесь функцией ЧАСТОТА подсчитывается лишь колонка Частота; колонки I и J следует вычислить вручную и построить график.

 

Рис. 2.79

 

Проделайте следующие действия:

1. Выделите диапазон H1:H14 и вызовите функцию ЧАСТОТА из группы Статистические и заполните параметры – рис. 2.80. После нажатия ОК встаньте на строку формул и нажмите Ctrl+Shift+Enter. Карманы будут заполнены частотами появления значений.

2. В ячейку H15 введите формулу вычисления общего числа испытаний n: =СУММ(H2:H14).

3. В ячейку I2 введите формулу вычисления статистической частоты =I2/H$15 и размножьте ее на весь диапазон I3:I14.

4. В ячейку J2 запишите значение из I2, в ячейку J3 – формулу =J2+I3, которую следует размножить на весь диапазон J4:J14.

5. Выделите диапазон I2:J14 для построения графика и вызовите мастер диаграмм: выберите нестандартный тип График | гистограмма 2. Построенный график (рис. 2.81) должен быть идентичен предыдущему (рис. 2.78).

 

Рис. 2.80

 

Рис. 2.81

 

 

Расчет элементарных статистических характеристик

 

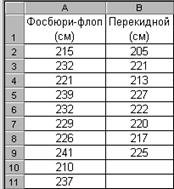
При обработке случайных выборок в первую очередь вычисляют их числовые параметры, характеризующие тенденции, разброс и изменчивость данных. Их можно рассчитывать как с помощью перечисленных в предыдущих разделах функций, так и с применением инструмента Описательная статистика из Пакета анализа, который позволяет получить единый статистический отчет по всем характеристикам входных данных.

Применим инструмент Описательная статистика к выборкам сезонных результатов двух прыгунов в высоту разными способами: фосбюри-флопом и перекидным – рис. 2.82.

 

Рис. 2.82

 

Вызовите инструмент Описательная статистика через меню С е рвисàАна л из данных…. На рис. 2.83 показано заполнение параметров инструмента. Входной интервал $А$2:$D$11 - это диапазон анализируемых данных. Здесь данные выборки расположены по столбцам, поэтому установлен переключатель По столбцам. Выходной интервал $D$1 – это ячейка, начиная с которой будет выведен результат. Установите также флажок Итоговая статистика - в выходном интервале для каждого столбца будут рассчитаны все статистические показатели. Поле Уровень надежности позволяет установить требуемый уровень доверительной вероятности; по умолчанию 95%, что соответствует уровню значимости 0.05. Результат работы инструмента показан на рис. 2.84.

 

Рис. 2.83

 

Рис. 2.84