Определение доверительных интервалов

 

Важная характеристика выборки – среднее арифметическое – обычно не совпадает со средним арифметическим генеральной совокупности. Поэтому актуальным является определение приемлемых границ изменения среднего арифметического выборок – доверительного интервала среднего. Для этого вычисляют средние арифметические нескольких выборок; вычисленные значения рассматривают как случайные величины, распределенные по нормальному закону относительно среднего арифметического генеральной совокупности. Известно, что в пределы [m-r,m+r] нормально распределенная случайная величина попадает с доверительной вероятностью 0,683 (68.3%) в пределы [m-2r,m+2r] - с вероятностью 0,955 (95.5%), в пределы [m-3r,m+3r] - с вероятностью 0,997 (99.7%) – где m среднее, а r стандартное отклонение от среднего (рис. 2.71).

Инструмент Описательная статистика вычисляет полный доверительный интервал выборки: на рис. 2.84 он равен 31. Таким образом, можно утверждать, что в 95% случаев значения выборки попадут в доверительный интервал [228.2-15.5, 228.2+15.5].

Функция ДОВЕРИТ вычисляет полуширину доверительного интервала среднего по заданному уровню значимости, стандартному отклонению и числу значений в выборке. Пусть требуется найти границы доверительного интервала для среднего с 95% надежностью (уровень значимости a=0.05) для 50 отправлений по электронной почте, если известно среднее время доставки сообщения m =30сек, стандартное отклонение r =3сек.

Введите статистическую функцию ДОВЕРИТ и заполните параметры, как показано на рис. 2.85. После нажатия ОК, вы получите значение ДОВЕРИТ(0,05;3;50)=0.83154. Это означает, что с уверенностью 95% среднее арифметическое времени доставки сообщения по E-mail для генеральной совокупности будет находиться в интервале [30-0.83154, 30+0.83154].

 

Рис. 2.85

 

ДОВЕРИТ(0,01;3;50) = 1.09283

ДОВЕРИТ(0,05;5;50) = 1.3859

ДОВЕРИТ(0,05;3;150) = 0.48009

 

Выше рассчитаны доверительные интервалы среднего для различных значений параметров. Как видно, доверительный интервал шире для б о льших значений уровня значимости a и стандартного отклонения r; и – у же при б о льшем размере выборки.

 

 

Подбор типа распределения

 

Одной из задач статистического анализа является оценка степень соответствия выборки известному теоретическому распределению, в частности нормальному распределению. Для этих целей применяют:

- графический метод, позволяющий визуально оценить меру соответствия; например, график на рис. 2.81 напоминает форму нормальной кривой и при большом объеме (>50) выборки совпадения/расхождения более очевидны;

- числовые характеристики асимметрию и эксцесс; асимметрия характеризует степень несимметричности распределения относительно среднего вправо (>0) и влево (<0); эксцесс характеризует степень остроконечности (>0) или сглаженности (<0) «хвостов» распределения; можно говорить о нормальности распределения, если асимметрия находится в интервале [–0.2;+0.2], а эксцесс – в интервале [2;4];

- критерии согласия, в частности ХИ-квадрат, который вычисляет вероятность совпадения выборки с нормальным распределением (функция ХИ2ТЕСТ в Excel).

Рассмотрим применение функции ХИ2ТЕСТ, дающей наиболее убедительную оценку меры соответствия выборки нормальному распределению. Если вычисленная вероятность совпадения ниже 0.95 (95%), то выборка не соответствует нормальному распределению, если выше 0.95, то можно утверждать о нормальном законе распределения выборки.

Поскольку критерий ХИ-квадрат основан на сравнении частот интервалов, то для функции ХИ2ТЕСТ должны быть предварительно подготовлены выборочное и теоретическое распределения частот по интервалам с помощью функции ЧАСТОТА или инструмента Гистограмма. На рис. 2.86 дана некоторая выборка, к ней вычислены частоты и теоретические частоты, на основе которых вычислена вероятность совпадения распределений 0.989531786. Это значение говорит о высокой степени соответствия выборки нормальному распределению.

 

Рис. 2.86

 

Последовательность действий результата на рис. 2.86 следующая:

1. Введите исходные данные в ячейки А3:Е14. В колонке G введите интервалы карманов и с помощью функции ЧАСТОТА в колонке H вычислите относительные частоты значений выборки.

2. В ячейке Н15 вычислите размер выборки (=СУММ(H2:H14)), в ячейке Н16 – среднее арифметическое выборки (=СРЗНАЧ(A3:E14)), в ячейке Н17 – стандартное отклонение (=СТАНДОТКЛОН(A3:E14)).

3. В колонке I вычислите статистические вероятности – это необходимо для дальнейшего графического сравнения выборочного распределения вероятностей с теоретическим. В ячейку I3 запишите формулу =H2/H$15, затем размножьте ее на диапазон I4:I14.

4. По вычисленным в п.2 данным постройте теоретическое нормальное распределение вероятностей, для чего в ячейку J3 запишите функцию =НОРМРАСП(G2;H$16;H$17;0). Затем размножьте ее на диапазон J4:J14.

5. В колонке К вычислите теоретические частоты: в ячейку К3 запишите формулу =J2*H$15 и размножьте ее на диапазон К4:К14.

6. В ячейку К17 введите функцию ХИ2ТЕСТ. Параметры функции показаны на рис. 2.87.

 

Рис. 2.87

 

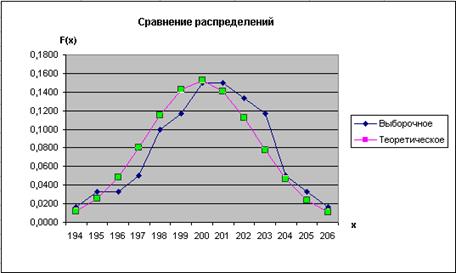
Для графической оценки постройте графики выборочного (I4:I14) и теоретического (J4:J14) распределения вероятностей – рис. 2.88. Сравнение графиков не опровергает результата работы функции ХИ2ТЕСТ: выборка в целом соответствует нормальному распределению

 

Рис. 2.88

 

Функцию ХИ2ТЕСТ применяют также в случаях, когда требуется выявить наличие различий между выборками, а закон распределения данных неизвестен. При этом обычно известны лишь расчетные, теоретические значения, которые принимают за генеральную совокупность. Вычисляется вероятность случайного появления значений в выборках: если вероятность p меньше уровня значимости a=0.05, то различия между выборками не случайны и делают вывод о достоверном отличии (независимости) выборок друг от друга (уровень значимости a – максимальное значение вероятности, при котором появление события практически невозможно).

 

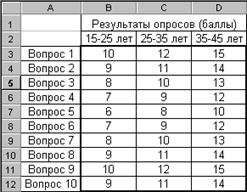
Рис. 2.89

 

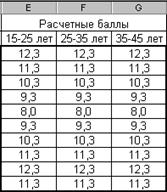
На рис. 2.89 приведены результаты опроса трех возрастных групп в баллах. Необходимо определить, есть ли достоверные отличия в ответах в группах.

Поскольку ожидаемые значения не заданы, то в качестве ожидаемых, рассчитаем средние значения трех выборок по каждому вопросу, которые и примем за генеральную совокупность – рис. 2.90.

Рис. 2.90

 

Далее применим функцию =ХИ2ТЕСТ(B3:D12;E3:G12). Результат 0.868486 (>0.05) говорит о том, что различия между выборками случайны и не выявлено достоверных отличий выборок друг от друга.