
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал для значений зависимой переменнойСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
50. Проверка гипотез относительно параметров линейной регрессии Рассмотрим критерии проверки гипотез относительно параметров a, b и Заметим, что проверку некоторых гипотез можно связать с построением доверительных интервалов. Пусть, например, проверяется гипотеза H0: Для проверки гипотезы H0: b=b0 против H1: b ≠ b0 используется статистика
которая при справедливости нулевой гипотезы имеет распределение Стьюдента с n − 2 степенями свободы. Если расчетное значение статистики Т
51. Сравнение двух линий регрессии путем сравнения параметров регрессионной модели Часто требуется сравнить линии регрессии, рассчитанные по двум выборкам. Это можно сделать тремя способами: ü Сравнить коэффициенты наклона b ü Сравнить коэффициенты сдвига a ü Сравнить линии в целом
где b 1– b 2 — разность коэффициентов наклона, a sb 1– b 2 — ее стандартная ошибка. Затем вычисленное значение t сравнивают, с критическим значением, имеющим n 1+ n 2–4 степени свободы. Если обе регрессии оценены по одинаковому числу наблюдений, то стандартная ошибка разности
Если же объемы выборок различны, следует воспользоваться объединенной оценкой остаточной дисперсии
Тогда стандартная ошибка разности
где a 1– a 2 — разность коэффициентов сдвига, a sa 1– a 2 — стандартная ошибка разности коэффициентов сдвига Затем вычисленное значение t сравнивают, с критическим значением, имеющим n 1+ n 2–4 степени свободы. Сравнить две линии регрессии — значит оценить вероятность нулевой гипотезы о совпадении линий. Коэффициенты регрессии вычисляются так, чтобы разброс точек вокруг линии регрессии был минимален. Разброс этот характеризуется остаточной дисперсией s 02: чем меньше остаточная дисперсия, тем лучше прямая регрессии соответствует имеющимся точкам. Следовательно объединив обе выборки в одну и построим для нее линию регрессии получим: в случае если линии регрессии для двух выборок близки, остаточная дисперсия при этом существенно не изменится. И наоборот, если они различаются, то совпадение точек и линии ухудшится и остаточная дисперсия возрастет. Таким образом порядок сравнения двух линии регрессии: ü Построить прямую регрессии для каждой из выборок. ü По остаточным дисперсиям ü Объединить обе выборки. Построить прямую регрессии для получившейся выборки и вычислить остаточную дисперсию Вычислить «выигрыш» от использования двух раздельных регрессий. Мерой выигрыша служит величина:
Сравнить вычисленное значение с критическим значением F для числа степеней свободы 2 и n 1+ n 2–4. Если полученное значение больше критического, то гипотеза о совпадении линий регрессии должна быть отклонена.
52. Сравнение двух линий регрессии в целом
53. Линия регрессии, проходящая через начало координат или другую фиксированную точку
Выражения для (1 − α) доверительного интервала для значения параметра b имеет вид:
Вычисления по проверки значимости регрессии с помощью дисперсионного анализа проводят следующим образом
распределена по закону Фишера с числом степеней свободы 1 и n −2. Нулевая гипотеза будет отклонена на уровне значимости α, если вычисленное значение статистики F будет больше α-процентной точки f 1; n −2;α распределения Фишера.
Подогнанная прямая имеет следующий вид:
54. Обратная простая регрессия В основе построения градировочных графиков, как правило, лежат методы линейной регрессии. Трудность построения и использования градуировок связана с так называемой проблемой обратной регрессии. Дело в том, что зависимая и независимая переменные меняются местами при использовании готового графика. То, что было независимой переменной, при измерении становится результатом, что порождает существенные проблемы. Предположим, что необходимо провести калибровку манометра (датчика давления) и при этом известно, что показания манометра являются линейной функцией давления:
Для калибровки манометра на него подают n контролируемых давлений xi (i = 1, 2,…, n) и считывают показания манометра yi. По этим данным подбирают уравнение
В то же время для x 0 можно рассчитать границы (1 − α) доверительного интервала:
где d 1 и d 2 – действительные несовпадающие корни уравнения:
Конечный доверительный интервал получается тогда и только тогда, когда
Если оценка x 0 не попадает в границы интервала и, то доверительная область для x 0 состоит их двух полупрямых. Если же уравнение не имеет действительных корней, то доверительная область совпадает во всей действительной прямой.
55. Множественная линейная регрессия Во многих практических задачах простая (однофакторная) линейная регрессия дает недостаточную информацию о зависимой переменной. Так, например, урожайность какой-либо культуры определяется несколькими факторами, такими как количество осадков, температура, влажность воздуха, физические и химические показатели почвы и т. д. В таких случаях обращаются к множественной регрессионной модели.
Предположения относительно множественной линейной регрессии аналогичны тем, которые применялись для простой линейной регрессии. В частности, что все xi считаются фиксированными и для любого набора xi значения yi распределены по нормальному закону с постоянной дисперсией.
после упрощений получается следующая система нормальных уравнений для нахождения оценок параметров:
Пусть b – вектор-столбец размера (k + 1), состоящий из коэффициентов b 0, b 1, …, b k, y – вектор-столбец из n наблюдений, ε – вектор-столбец из n ошибок и X – матрица наблюдений размером n (k + 1):
Тогда уравнение модели регрессии можно записать в виде:
Выражение для D можно представить в матричном виде:
тогда вектор оценок b получается из решения системы уравнений:
решение которой имеет вид:
Дисперсионный анализ множественной линейной регрессии проводится в следующей таблице:
56. Нелинейная регрессия Во многих случаях линейные по параметрам модели регрессии могут служить лишь в качестве первого приближения к истинной модели. Существует много ситуаций, в которых модели такого вида не пригодны. Если мы приходим к заключению, что модель имеет нелинейную форму, то необходимо воспользоваться для описания именно этой, а не более простой линейной моделью. Нелинейные модели можно подразделить на два класса, которые условно называются внутренне линейными и внутренне нелинейными. Если модель внутренне линейна, то с помощью подходящего преобразования ее можно привести к стандартной линейной модели.
где α и β – неизвестные параметры, ε – мультипликативная случайная ошибка, логарифмированием обеих частей уравнения может быть переведена в линейную форму
к которой можно применять стандартные методы исследования линейной регрессии. Однако следует подчеркнуть, что для того, чтобы критерий значимости и оценка доверительных интервалов были обоснованными, необходимо соблюдение условия: логарифмы ошибок должны подчиняться нормальному закону с нулевым математическим ожиданием и постоянной дисперсией.
является внутренне нелинейной, и поэтому общие методы линейной регрессии для этой модели непригодны. Если модель регрессии линейна, то оценки метода наименьших квадратов будут оптимальными, поскольку они являются несмещенными оценками с минимальной дисперсией. Но если модель нелинейна, то методы получения наилучших оценок параметров отсутствует. Однако если ошибки ε i представляют собой независимые случайные величины, распределенные нормально с нулевым математическим ожиданием и постоянной дисперсией, то с помощью метода наименьших квадратов могут быть получены оценки параметров уравнения регрессии, которые минимизируют сумму квадратов отклонений наблюдений от линии регрессии. Если в случае линейной модели оценки получаются из решения системы линейных уравнений, то в случае нелинейной модели приходится решать систему нелинейных уравнений и соответствующее решение уже нельзя представить в явном виде. По этой причине приходится использовать различные итерационные методы для численного определения оценок метода наименьших квадратов. Статистические методы линейной регрессии могут быть адаптированы для нелинейной регрессии, однако статистический анализ при этом будет приближенным.
57. Оценка результата измерения: Виды измерений Измерение определяется как “нахождение физической величины опытным путем с помощью специальных технических средств” Процесс измерения может быть определен как операция, посредством которой определяется отношение одной измеряемой величины к другой однородной величине, принимаемой за единицу. Величина, выражающая такое отношение, называется численным значением измеряемой величины. Различают следующие виды измерений физических величин: ü Прямые измерения ü Косвенные измерения ü Совместные измерения ü Совокупные измерения Прямыми называются измерения, при которых значения величины находят непосредственно из экспериментальных данных – результатов измерений. Косвенными называются такие измерения, при которых исследуемая величина определяется с помощью известных соотношений между физическими величинами, найденными в результате прямых измерений. Совместными называются одновременные измерения двух или нескольких не одноименных величин, характеризующих состояние исследуемого объекта, для нахождения зависимости между этими величинами. Совокупными называются измерения нескольких одноименных величин, при этом результаты измерений находят путем решения системы линейных уравнений
58. Оценка результата измерения: Погрешности измерений Погрешность измерения характеризует разность между измеренным и истинным значением величины Вероятность того, что погрешность измерения не превзойдет заданного значения характеризуется надежностью измерения. Погрешности измерений в общем случае вызываются действием большого числа факторов и могут быть разделены на две большие группы: ü Случайные погрешности ü Систематические погрешности Случайные погрешности обусловлены факторами, которые проявляются весьма нерегулярно и интенсивность появления которых трудно предвидеть
Оба вида погрешностей в процессе измерения проявляются в виде суммы:
Различают три вида систематических погрешностей: ü Первый вид – это систематические погрешности, величина которых может быть измерена экспериментально или вычислена, исходя из определенных теоретических соображений ü Второй вид систематических погрешностей – ошибки, о которых известно либо предельное значение, либо среднеквадратическое отклонение ü Третий вид систематических погрешностей – это незамеченные в процессе измерений ошибки, о существовании которых неизвестно Формы представления погрешностей ü Абсолютные погрешности ü Относительные погрешности ü Приведенные погрешности
59. Обработка результатов наблюдений при прямых измерениях
Среднеквадратическое отклонение результата измерения оценивается по формуле
Если результаты наблюдений согласуются с нормальным распределением, тогда доверительные границы случайной погрешности результата измерения
60. Обработка результатов наблюдений при косвенных измерениях При косвенных измерениях исследуемая величина A не измеряется непосредственно, а должна рассчитываться на основании известной функциональной зависимости от одной или нескольких первоначально измеряемых величин
При этом каждая из оценок âj получена со своей погрешностью и требуется, зная эти погрешности, найти погрешность измерения величины A.
61. Обработка результатов наблюдений при совместных и совокупных измерениях Реализация этих видов измерений осуществляется на основе решения системы уравнений
В этом случае решение системы будет единственным и может быть представлено в виде:
Однако с целью уменьшения погрешности измерения проводят большое число наблюдений, чем количество измеряемых параметров. Тогда система уравнений может быть записана в виде:
62. Обработка результатов наблюдений, распределенных по закону Пуассона
Оценкой интенсивности потока будет величина
Если за время T зарегистрировано Nэ событий, то за оценку параметра l в распределении Пуассона следует взять значение зарегистрированных событий: l= Nэ
Для нахождения границ доверительных интервалов для различных значений оценки параметра l= Nэ составлены статистические таблицы
При λ > 15 распределение Пуассона достаточно хорошо аппроксимируется нормальным распределением с математическим ожиданием и дисперсией равными λ. Поэтому в экспериментальной работе для предварительной оценки погрешности числа отсчетов за одно измерение часто используют значение ± Nэ (68% доверительный интервал), ±2 Nэ (95% доверительный интервал) и ±3 Nэ (99.8% доверительный интервал)
63. Анализ временных рядов. Прогнозирование на основе моделей временных рядов 64. Анализ временных рядов. Сглаживание временного ряда
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.81.172 (0.009 с.) |

 Разброс значений складывается из разброса значений вокруг линии регрессии и неопределенности положения самой этой линии. Характеристикой разброса значений вокруг линии регрессии является оценка дисперсии s 02, а неопределенности положения линии регрессии дисперсия D [ Y | x 0]. Дисперсия суммы двух величин равна сумме дисперсий D [ Y ] = D [ Y | x 0]+ s 02, поэтому доверительный интервал для индивидуального значения Y 0 будет иметь вид
Разброс значений складывается из разброса значений вокруг линии регрессии и неопределенности положения самой этой линии. Характеристикой разброса значений вокруг линии регрессии является оценка дисперсии s 02, а неопределенности положения линии регрессии дисперсия D [ Y | x 0]. Дисперсия суммы двух величин равна сумме дисперсий D [ Y ] = D [ Y | x 0]+ s 02, поэтому доверительный интервал для индивидуального значения Y 0 будет иметь вид 2.
2. 0 с уровнем значимости, скажем 0.01, при альтернативной гипотезе H1:
0 с уровнем значимости, скажем 0.01, при альтернативной гипотезе H1:  ≠
≠  0. Тогда можно построить 0.99 доверительный интервал для параметра
0. Тогда можно построить 0.99 доверительный интервал для параметра 
 то гипотеза отвергается.
то гипотеза отвергается.
 Если нужно проверить, значимо ли различие в наклоне двух прямых регрессии, критерий Стьюдента t вычисляется по формуле:
Если нужно проверить, значимо ли различие в наклоне двух прямых регрессии, критерий Стьюдента t вычисляется по формуле:


 Аналогично сравниваются и коэффициенты сдвига a 1 и а 2. В этом случае
Аналогично сравниваются и коэффициенты сдвига a 1 и а 2. В этом случае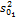 и
и  каждой из регрессий вычислить объединенную оценку остаточной дисперсии
каждой из регрессий вычислить объединенную оценку остаточной дисперсии 


 По
По  и
и 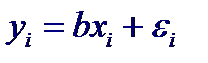 Предположим, что еще в начале исследования известно, что прямая регрессии должна пройти через начало координат, т. е. модель регрессии имеет вид
Предположим, что еще в начале исследования известно, что прямая регрессии должна пройти через начало координат, т. е. модель регрессии имеет вид В этом случае на основе n имеющихся наблюдений получается следующая оценка единственного параметра b (обозначим ее через B):
В этом случае на основе n имеющихся наблюдений получается следующая оценка единственного параметра b (обозначим ее через B): Несмещенной оценкой для σ 2 будет
Несмещенной оценкой для σ 2 будет

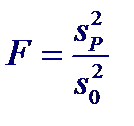 Если ошибки εi распределены по нормальному закону, то при справедливости гипотезы Н0: b = 0 статистика
Если ошибки εi распределены по нормальному закону, то при справедливости гипотезы Н0: b = 0 статистика Иногда априори известно, что прямая регрессии должна пройти через заданную точку на плоскости (x 0, y 0). Наиболее простой способ построения прямой в этом случае заключается в том, чтобы из каждого значения x вычесть x 0, а из каждого y вычесть y 0 и проделать выше описанную процедуру для линии регрессии проходящей через начало координат.
Иногда априори известно, что прямая регрессии должна пройти через заданную точку на плоскости (x 0, y 0). Наиболее простой способ построения прямой в этом случае заключается в том, чтобы из каждого значения x вычесть x 0, а из каждого y вычесть y 0 и проделать выше описанную процедуру для линии регрессии проходящей через начало координат.
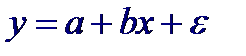 Что можно записать в виде уравнения:
Что можно записать в виде уравнения:
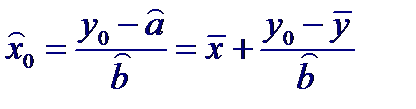 которое можно использовать для оценивания (предсказания) неизвестного давления x 0 при заданном показании манометра y 0
которое можно использовать для оценивания (предсказания) неизвестного давления x 0 при заданном показании манометра y 0



 Модель множественной линейной регрессии имеет следующий вид:
Модель множественной линейной регрессии имеет следующий вид: Для получения оценок параметров b 0, b 1,..., bk методом наименьших квадратов нужно минимизировать по этим параметрам выражение
Для получения оценок параметров b 0, b 1,..., bk методом наименьших квадратов нужно минимизировать по этим параметрам выражение Приравняв нулю частные производные
Приравняв нулю частные производные


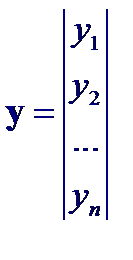




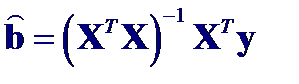
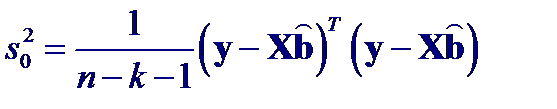 Несмещенной оценкой дисперсии является:
Несмещенной оценкой дисперсии является:
 Например, модель
Например, модель
 Другая модель
Другая модель Систематические погрешности обусловлены факторами, которые не изменяются или изменяются закономерно в процессе измерения
Систематические погрешности обусловлены факторами, которые не изменяются или изменяются закономерно в процессе измерения Описание случайной погрешности полностью определяется законом ее распределения, в качестве которого может выступать, например, нормальный закон
Описание случайной погрешности полностью определяется законом ее распределения, в качестве которого может выступать, например, нормальный закон Случайная погрешность представляет собой разность между результатом единичного измерения x и математическим ожиданием результатов наблюдений
Случайная погрешность представляет собой разность между результатом единичного измерения x и математическим ожиданием результатов наблюдений Систематическая погрешность представляет собой отклонение математического ожидания результатов наблюдений от действительного (истинного) значения, скажем a, измеряемой величины:
Систематическая погрешность представляет собой отклонение математического ожидания результатов наблюдений от действительного (истинного) значения, скажем a, измеряемой величины:
 В этом случае необходимо оценить математическое ожидание (истинное значение) A по набору результатов наблюдений:
В этом случае необходимо оценить математическое ожидание (истинное значение) A по набору результатов наблюдений: За результат измерения (оценку математического ожидания A) принимают
За результат измерения (оценку математического ожидания A) принимают
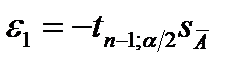

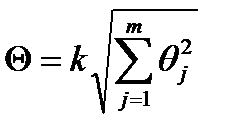 При равномерном распределении неисключенных систематических погрешностей границы этих погрешностей
При равномерном распределении неисключенных систематических погрешностей границы этих погрешностей
 Доверительные границы погрешности результата измерения
Доверительные границы погрешности результата измерения Здесь
Здесь
 Вычислить результат косвенного измерения
Вычислить результат косвенного измерения
 Найти оценку неисключенной систематической составляющей погрешности результата косвенного измерения
Найти оценку неисключенной систематической составляющей погрешности результата косвенного измерения Например необходимо измерить параметры R 0, α, β характеризующие зависимость сопротивление образца от температуры. С этой целью проводится измерение сопротивления при трех значениях температуры и составляется система уравнений.
Например необходимо измерить параметры R 0, α, β характеризующие зависимость сопротивление образца от температуры. С этой целью проводится измерение сопротивления при трех значениях температуры и составляется система уравнений.






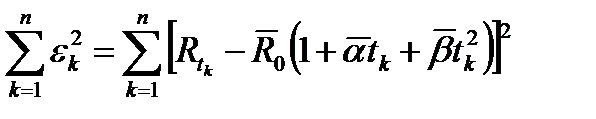 Тогда оценки параметров можно найти методом наименьших квадратов, при котором добиваются минимума погрешности:
Тогда оценки параметров можно найти методом наименьших квадратов, при котором добиваются минимума погрешности: Случайный процесс удовлетворяющий условиям ординарности, стационарности и отсутствия последействия называется пуассоновским и для него вероятность наступления за время t ровно n событий описывается законом распределения Пуассона
Случайный процесс удовлетворяющий условиям ординарности, стационарности и отсутствия последействия называется пуассоновским и для него вероятность наступления за время t ровно n событий описывается законом распределения Пуассона



