
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цель написания и назначение книгиСодержание книги
Поиск на нашем сайте
Козлов В.Г. Техническая эксплуатация радиоэлектронного оборудования. Учебное пособие по практическим занятиям и лабораторным работам для студентов специальности 160905 – «Техническая эксплуатация транспортного радиооборудования». Томск: Томский государственный университет систем управления и радиоэлектроники, 2007. - 107 с.
В разделе пособия «Решение задач по технической эксплуатации радиоэлектронного радиооборудования на практических занятиях» приведены основные расчетные формулы, примеры решения типовых задач и многовариантные задачи для самостоятельной работы. Рассмотрены вопросы расчета периодичности и продолжительности профилактических работ и расчета ремонтопригодности. Остальные вопросы, изучаемые на практических занятиях по дисциплине «Техническая эксплуатация радиоэлектронного оборудования (ТЭРЭО)» и не вошедшие в пособие из-за его ограниченного объёма, планируется издать в дальнейшем. Представлены описания четырех лабораторных работ и индивидуальные задания для их выполнения. Кроме того, отдельно даны описания и индивидуальные задания двух лабораторных работ по технической эксплуатации, в которых используется математический аппарат теории массового обслуживания. Это связано с тем, что «Теория массового обслуживания», являющаяся разделом ТЭРЭО, изучается на кафедре КИПР ТУСУР как отдельная дисциплина. При выполнении лабораторных работ предполагается широкое использование системы схемотехнического моделирования MicroCAP 8 и пакета прикладных программ MathCAD 13. Учебное пособие по практическим занятиям и лабораторным работам составлено для студентов очной, заочной и дистанционной форм обучения по специальности 160905 – «Техническая эксплуатация транспортного радиооборудования», но может быть использовано и студентами других специальностей радиотехнического профиля.
Ó Томский государственный университет систем управления и радиоэлектроники, Ó Козлов В.Г., 2007 содержание 1 введение..................................................................................... 6 1.1 Цель написания и назначение книги........................................ 6 1.2 Основные термины и определения технической эксплуатации радиоэлектронного оборудования и задачи, решаемые при эксплуатации............................................................................. 7 2 Решение задач по технической эксплуатации радиоэлектронного оборудования на практических занятиях................................................... 10 2.1 Расчет периодичности и продолжительности профилактических работ....................................................... 10 2.1.1 Основные соотношения между периодом профилактических работ и средней продолжительностью технического обслуживания........ 10 2.1.2 Примеры расчета периодичности и продолжительности профилактических работ.................................................. 12 2.1.3 Задачи расчета периодичности и продолжительности профилактических работ.................................................. 15 2.2 Расчёт ремонтопригодности................................................... 17 2.2.1 Основные формулы для расчёта ремонтопригодности.. 17 2.2.2 Примеры расчета ремонтопригодности.......................... 19 2.2.3 Задачи по расчёту ремонтопригодности......................... 22 3 Описания лабораторных работ по технической эксплуатации радиоэлектронного оборудования и индивидуальные задания для их выполнения 24 3.1 Составление алгоритма для определения места неисправности радиоэлектронного оборудования.............. 24 3.1.1 Цели работы...................................................................... 24 3.1.2 Общие теоретические сведения........................................ 24 3.1.3 Задание на работу............................................................. 30 3.1.4 Содержание отчета........................................................... 30 3.1.5 Перечень контрольных вопросов, которые могут быть заданы во время защиты отчёта по работе.................................................. 30 3.1.6 Варианты заданий............................................................. 31 3.2 Граничные испытания для оценки запаса параметрической надежности 32 3.2.1 Цель работы...................................................................... 32 3.2.2 Общие сведения о параметрической надёжности............ 32 3.2.3 Методика проведения граничных испытаний для оценки запаса параметрической надежности........................................... 33 3.2.4 Задание на работу............................................................. 38 3.2.5 Содержание отчета........................................................... 39 3.2.6 Перечень контрольных вопросов, которые могут быть заданы во время защиты отчёта по работе.................................................. 39 3.3 Функциональные испытания математической модели радиоэлектронного устройства в системе MicroCAP 8 с использованием метода планирования полного факторного эксперимента........................................ 40 3.3.1 Цели работы...................................................................... 40 3.3.2 Общие сведения о планировании факторного эксперимента и его применении при функциональных испытаниях 40 3.3.3 Пример получения полиноминальной модели с проверкой адекватности модели и значимости коэффициентов 47 3.3.4 Пример получения полиноминальной модели с помощью ПФЭ с вычислением коэффициентов взаимодействия 2-го порядка 55 3.3.5 Лабораторное задание...................................................... 71 3.3.6 Содержание отчета........................................................... 73 3.3.7 Перечень контрольных вопросов, которые могут быть заданы во время защиты отчёта по работе.................................................. 73 3.4 Сравнительные функциональные испытания стабильности выходного параметра математических моделей усилительных каскадов при изменении температуры эксплуатации в широком диапазоне................................................................ 74 3.4.1 Цель работы...................................................................... 74 3.4.2 Краткие сведения о стабильности выходного параметра усилительных каскадов при изменении температуры эксплуатации в широком диапазоне.......................................................... 74 3.4.3 Пример проведения сравнительных функциональных испытаний стабильности выходного параметра................................ 77 3.4.4 Лабораторное задание...................................................... 86 3.4.5 Содержание отчета........................................................... 87 3.4.6 Перечень контрольных вопросов, которые могут быть заданы во время защиты отчёта по работе.................................................. 87 4 Описания и индивидуальные задания лабораторных работ по технической эксплуатации, в которых используется математический аппарат теории массового обслуживания....................................................................... 88 4.1 Определение статистических характеристик технического обслуживания замкнутой системы массового обслуживания с ожиданием............................................................................ 88 4.1.1 Цель работы...................................................................... 88 4.1.2 Общие сведения о применении теории массового обслуживания для определения статистических характеристик технического обслуживания........................................................................................... 88 4.1.3 Пример использования ТМО для расчета характеристик технического обслуживания замкнутой многоканальной СМО с ожиданием......................................................................... 92 4.1.4 Индивидуальные задания для расчета в лабораторной работе характеристик технического обслуживания замкнутой многоканальной СМО с ожиданием............................................................. 94 4.1.5 Этапы выполнения лабораторной работы...................... 95 4.1.6 Содержание отчета........................................................... 96 4.1.7 Перечень контрольных вопросов, которые могут быть заданы во время защиты отчёта по работе.................................................. 96 4.2 Определение статистических характеристик технического обслуживания открытых систем массового обслуживания с ожиданием и с отказами 96 4.2.1 Цель работы...................................................................... 96 4.2.2 Общие сведения о СМО с ожиданием и с отказами........ 97 4.2.3 Общие сведения об открытой одноканальной СМО с ожиданием 97 4.2.4 Общие сведения об открытой многоканальной СМО смешанного типа с ограниченным временем ожидания............................... 100 4.2.5 Общие сведения об открытой многоканальной СМО смешанного типа с ограничением по длине очереди.................................... 101 4.2.6 Индивидуальные задания для расчета в лабораторной работе характеристик технического обслуживания открытых многоканальных СМО с ожиданием и с отказами.................................................................... 103 4.2.7 Этапы выполнения лабораторной работы.................... 105 4.2.8 Содержание отчета......................................................... 105 4.2.9 Перечень контрольных вопросов, которые могут быть заданы во время защиты отчёта по работе................................................ 105 Список литературы............................................................... 106 Введение Решение задач по технической эксплуатации радиоэлектронного оборудования на практических занятиях Расчет периодичности и продолжительности профилактических работ Примеры расчета периодичности и продолжительности профилактических работ
Пример 2.1. Передатчик работает в субботу и воскресенье по 4 ч в сутки, а в остальные дни – по 6 ч в сутки. Длительность профилактических работ по отдельным узлам передатчика в среднем составляют: по антенно-фидерному тракту – 1.5 ч, по остальным высокочастотным узлам – 2.5 ч, по блоку питания – 1 ч. Интенсивность отказов передатчика при проведении профилактических работ lР = 2×10-3 ч-1. Определить оптимальный период профилактических работ. Отказами в выключенном состоянии пренебречь. Решение: а) с помощью выражения (2.6) вычислим коэффициент эффективности эксплуатации:
б) с помощью выражения (2.11) находим среднюю продолжительность ТО:
в) по формуле (2.8) определим оптимальный период профилактических работ:
Ответ: оптимальный период профилактических работ tТО = 148.7 ч. Пример 2.2. Наработка на отказ бортового радиолокатора при экспоненциальном законе надежности и без проведения профилактических работ составила Т 0 = 300 ч. При проведении профилактических работ длительностью Т ТО = 5 ч наработка на отказ составила 900 ч. Среднее время ремонта Т Р = 6 ч. Коэффициент интенсивности эксплуатации К И = 0.25. Интенсивность отказов в выключенном состоянии lХР = 2×10-6 ч-1. Определить оптимальный период проведения профилактических работ, а также коэффициент готовности и коэффициент оперативной готовности для t = 2 ч без профилактики и при проведении профилактики. Решение: а) экспоненциальное распределение применяется не только к неремонтируемым объектам, но и к ремонтируемым объектам с простейшими потоками отказов; с учетом этого находим интенсивность отказов радиолокатора без проведения профилактических работ:
и при проведении профилактических работ:
б) находим оптимальный период проведения профилактических работ по формуле (2.7):
в) находим коэффициенты готовности, равные вероятности того, что объект окажется работоспособным в произвольный момент времени, кроме периодов плановых ремонтов, плановых ТО и других плановых мероприятий, прерывающих эксплуатацию объекта по назначению: 1) коэффициент готовности без проведения профилактики:
2) коэффициент готовности при проведении профилактики:
г) находим коэффициенты оперативной готовности, равные вероятности того, что объект окажется работоспособным в произвольный момент времени, и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени: 1) коэффициент оперативной готовности без проведения профилактики:
2) коэффициент оперативной готовности при проведении профилактики:
Ответ: оптимальный период проведения профилактических работ tТО = 189.3 ч; коэффициенты готовности без проведения профилактики К Г = 0.98, а при проведении профилактики К ГП = 0.993; коэффициенты оперативной готовности без проведения профилактики К ОГ = 0.973, а при проведении профилактики К ОГП = 0.991. Пример 2.3. Для посадки на планеты с высокой температурой поверхности (больше 500оС) разработана специальная приёмо-передающая телевизионная система, которая незадолго до посадки охлаждается, затем работает на поверхности планеты менее получаса, после чего из-за сильного разогрева переходит в неработоспособное состояние. В системе используются современные высокостабильные интегральные схемы и цифровая обработка информации. Интенсивность отказов системы при охлаждении lХР = 3×10-6 ч-1. Длительность профилактических работ по отдельным узлам системы в среднем составляют: по антенно-фидерному тракту – 2 ч, по приёмному тракту – 1.5 ч и по передающему тракту – 3 ч. По результатам испытаний получено численное значение поправочного коэффициента, учитывающего высокую стабильность параметров станции, К СТ = 1.5. Определить оптимальный период проведения профилактических работ. Решение: а) находим среднюю продолжительность ТО:
б) определяем оптимальный период проведения профилактических работ для аппаратуры одноразового действия:
в) определяем оптимальный период проведения профилактических работ с учётом поправочного коэффициента К СТ: tТОC = К СТtТО = 1.5×2082 = 3123 ч. Ответ: оптимальный период проведения профилактических работ tТОC = 3123 ч.
Таблица 2.1 – Исходные данные для задачи 2.1
Таблица 2.2 – Исходные данные для задачи 2.2
Таблица 2.3 – Исходные данные для задачи 2.3
Расчёт ремонтопригодности Примеры расчета ремонтопригодности
Пример 2.4. Из-за возникших в системе n = 10 отказов на восстановление работоспособности было затрачено 20 ч. Определить доверительный интервал параметра Т Р с доверительной вероятностью Р (Î) = 0.95 при экспоненциальном распределении времени ремонта. Решение: а) определяем среднюю продолжительность ремонта:
б) по таблице 2.4 определяем при n = 10 и Р (Î) = 0.95 r 1 = 1.83 и r 2 = 0.64, а затем по формулам (2.21) и (2.22) определяем доверительные границы и интервал I Î изменения: T РН = T Р× r 2 = 2×0.64 = 1.28 ч; T РВ = T Р× r 1 = 2×1.83 = 3.66 ч; I Î = 1.28…3.66 ч. Ответ: доверительный интервал I Î = 1.28…3.66 ч. Пример 2.5. Имеется непрерывно работающая двухканальная линия связи. Интенсивность отказа λ и время ремонта канала имеют экспоненциальное распределение с параметром λ= 10-2 ч-1 и интенсивностью ремонта μ = 1 ч-1. Определить среднее значение суммарного времени ремонта линии и доверительный интервал I Î с вероятностью Р (Î) = 0.99 за время эксплуатации 2000 ч. Для восстановления имеется одна бригада. Вероятность отказа двух каналов одновременно Р 1,2 = 0.25. Ремонт отказавшего канала требует выключения всей линии. Решение: а) находим наработку на отказ одного канала: Т 0 = 1/λ = 1/10-2 = 100 ч; б) находим количество отказов в одном из каналов (n 1или n 2), суммарное количество отказов в каналах (n å)и количество отказов одновременно в двух каналах (n 1,2): n 1 = n 2 = t / T 0 = 2000/100 = 20; n å = n 2 + n 1 = 20 + 20 = 40; n 1,2 = n å× P 12 = 40×0.25 = 10; в) находим среднее время ремонта: 25% всех отказавших изделий (n 1,2) восстанавливаются поочередно за время:
Остальные 75% отказавших изделий (N 1 = n å - n 1,2 = 40 – 10 = 30) восстанавливаются за время: T Р1 = 1/μ = 1/1 = 1 ч. Среднее время ремонта линии:
г) по таблице 2.4 определяем для n = 40 и Р (Î) = 0.99, что r 1 = 1.5 и r 2 = 0.71, а затем по формулам (2.21) и (2.22) определяем доверительные границы и интервал I Î изменения времени ремонта Т Р: T РН = TР × r 2 = 1.25×0.71 = 0.89 ч; T РВ = TР × r 1 = 1.25×1.5 = 1.88 ч; I Î = 0.89…1.88 ч. Ответ: среднее значение суммарного времени ремонта линии T Р = 1.25 ч; доверительный интервал I Î = 0.89…1.88 ч. Пример 2.6. При эксплуатации устройства было зарегистрировано n = 30 отказов. Данные по распределению отказов по группам элементов и времени, затраченному на ремонт, приведены в таблице 2.6. Найти среднее время ремонта устройства и доверительный интервал при Р (Î) = 0.9, если распределение времени ремонта подчиняется закону Эрланга.
Таблица 2.6 – Исходные данные для примера 2.6
Решение: а) определяем среднее время ремонта: - для полупроводниковых приборов: T Р1 = 456/6 = 76 мин; - для электровакуумных приборов (ЭВП): T Р2 = 430/10 = 43 мин; - для микромодулей: T Р3 = 102/4 = 25.5 мин; - для резисторов и конденсаторов: T Р4 = 462/7 = 66 мин; - для прочих элементов: T Р5 = 366/3 = 122 мин; б) рассчитаем среднее время ремонта устройства:
где T Р i – среднее время ремонта элементов i -ой группы; Рi – вес (вероятность) отказов по группам элементов. Подставляя числовые данные, получим: T Р = (76×0.2 + 43×0.33 + 25.5×0.14 + 66×0.23 + 122×0.1)» 60 мин; в) по таблице 2.5 при n = 30 и Р (Î) = 0.9 находим d1 = 0.835 и d2 = 1.22 и с учётом формул (2.24) и (2.25) находим нижнюю и верхнюю доверительные границы времени ремонта Т Р и доверительный интервал I Î времени ремонта: T РН = T Р/d2 = 60/1.22 = 49.18 мин; T РВ = T Р/d1 = 60/0.835 = 71.86 мин; I Î = 49.18…71.86 мин. Ответ: среднее время ремонта устройства T Р = 60 мин; доверительный интервал I Î = 49.18…71.86 мин.
Таблица 2.7 – Исходные данные для задачи 2.4
Задача 2.5. Определить объём испытаний n при условии, что оценка среднего времени ремонта с вероятностью Р (Î) не отличалась бы от верхней доверительной границы более чем в k раз при заданном законе распределения времени ремонта. Вид закона и численные значения исходных величин для расчёта даны в таблице 2.8 и зависят от номера варианта.
Таблица 2.8 – Исходные данные для задачи 2.5
3 Описания лабораторных работ по технической эксплуатации радиоэлектронного оборудования и индивидуальные задания для их выполнения 3.1 Составление алгоритма для определения места неисправности радиоэлектронного оборудования Цели работы
- обучить студентов разработке информационной функциональной диагностической модели (ФДМ), графоаналитической модели и матрицы состояний, описывающих функционирование радиоэлектронного оборудования; - обучить студентов практически использовать методику составления алгоритма для поиска места неисправности радиоэлектронного оборудования, используя матрицы состояний и функции предпочтения; - обучить студентов практически использовать методику составления алгоритма для поиска места неисправности радиоэлектронного оборудования, используя метод половинного деления.
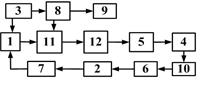
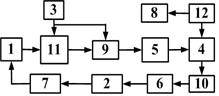
Рисунок 3.1 – Функциональная схема Рисунок 3.2 – Функциональная диагностическая модель Рисунок 3.3 – Ориентированный граф функциональной диагностической модели типового автоматического радиокомпаса
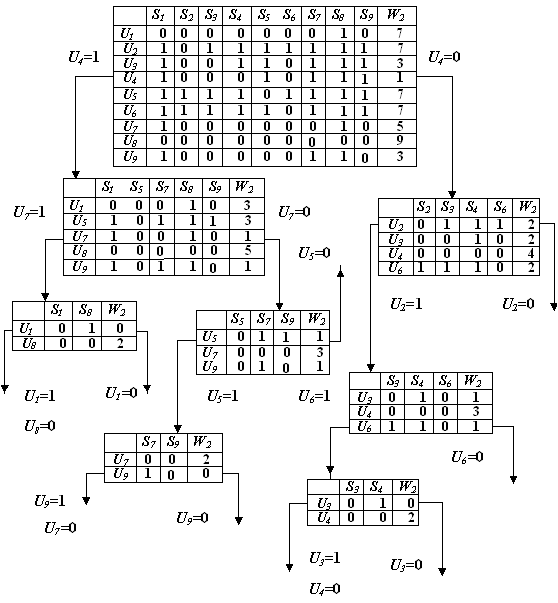
Рисунок 3.4 – Матрица состояний, построенная по ориентированному графу функциональной диагностической модели для Рисунок 3.5 – Структурная схема алгоритма поиска места отказа Задание на работу
Используя вариант функциональной схемы устройства, выданный преподавателем: а) разработать информационную функциональную диагностическую модель, графоаналитическую модель и матрицу состояний, описывающие функционирование устройства; б) составить алгоритм поиска места неисправности устройства, используя матрицы состояний, функции предпочтения и метод половинного деления.
Содержание отчета
1. Цель работы. 2. Описание и изображение информационной функциональной диагностической модели, графоаналитической модели и матрицы состояний, описывающих функционирование устройства, а также структурной схемы алгоритма поиска места неисправности. 3. Заключение – выводы по результатам работы.
Варианты заданий
Вариант 1↓ Вариант 2↓
Вариант 3↓ Вариант 4↓
Вариант 5↓ Вариант 6↓
Вариант 7↓ Вариант 8↓
Вариант 9↓ Вариант 10↓
Цель работы
Ознакомить студентов с методикой проведения граничных испытаний математической модели применительно к стабилизатору напряжения бортовой радиостанции для оценки запаса параметрической надежности при изменении температуры эксплуатации в широком диапазоне с использованием системы MicroCAP 8.
Рисунок 3.8 – Отображение режима работы математической модели Рисунок 3.10 – График, отображающий результаты граничных испытаний стабилизатора напряжения при номинальном напряжении питающей сети 27В (область безотказной работы заштрихована) Таким образом, проведение граничных испытаний дополнительно позволяет определить коэффициенты влияния АХi элементов Хi изделия на его выходной параметр N и составить уравнение погрешностей:
где Δ Хi – отклонение от номинального значения величины параметра элемента Хi; n – количество элементов в изделии; Δ N – отклонение от номинального значения величины выходного параметра N. Переход от погрешностей Δ N / N и Δ Хi / Хi к допускам на параметры δ N и δ Хi даётся уравнением:
Трудоемкость и затраты времени при проведении граничных испытаний с использованием компьютерной системы схемотехнического моделирования MicroCAP 8 значительно меньше, чем при обычных испытаниях. Намного легче производить изменение параметров элементов. Выдача напряжений и токов для всех элементов, а также построение графиков их частотных и временных зависимостей производится на экране монитора практически мгновенно. Кроме того, при использовании компьютерного моделирования модели являются виртуальными. Поэтому исключаются затраты на изготовление образца для испытаний, а также не требуется производить замену элементов при их отказе. Справедливости ради, следует отметить и трудности использования компьютерного моделирования, связанные с ограниченностью количества математических моделей элементов в библиотеке MicroCAP 8, а также с ограничением максимального количества элементов в исследуемых моделях. Однако в перспективе во многих случаях испытания на компьютерных моделях вытеснят обычные испытания.
Задание на работу
а) отобразить режим работы математической модели стабилизатора напряжения на 18В на экране монитора компьютера и добиться нормального функционирования этой модели в системе MicroCAP 8; б) в системе MicroCAP 8 провести граничные испытания для оценки запаса параметрической надежности применительно к математической модели стабилизатора напряжения на 18В бортовой (самолётной) радиостанции. В качестве параметров граничных испытаний выбрать напряжение питания V 1, изменяемое от 24В до 30В и температуру окружающей среды, изменяемую от –600С до +600С. В качестве изменяемых входных параметров выбрать сопротивления резисторов Ri, указанных преподавателем. В области безотказной работы выходное напряжение на резисторе R 11 не должно превышать граничных значений 18В± 5% (±0.9В). Для резисторов Ri построить графики, отображающие результаты граничных испытаний стабилизатора напряжения при номинальном напряжении питающей сети U 1 = 27Ви изменении температуры окружающей среды, и графики, отображающие результаты граничных испытаний при изменении напряжения питания U 1 от 24В до 30В при температуре окружающей среды +270С; в) по результатам граничных испытаний вычислить коэффициенты АRi влияния изменения сопротивлений Ri на выходное напряжение UR 11 на резисторе R 11, заменив в формуле (3.5) R 1 на Ri; г) составить уравнение погрешностей для
Содержание отчета
1. Цель работы. 2. Описание методики и проведение граничных испытаний. 3. Графики, отображающие результаты граничных испытаний, вычисление коэффициентов АRi. Составленное уравнение погрешностей для 4. Выводы по работе.
Цели работы
- обучение студентов составлению планов полного факторного эксперимента (ПФЭ); - обучение студентов проведению функциональных испытаний математической модели РЭУ в системе MicroCAP 8 с использованием метода планирования полного факторного эксперимента при изменении температуры, напряжения питания и параметров элементов в процессе эксплуатации; - обучение студентов обработке результатов ПФЭ с целью получения математического описания функционирования РЭУ в виде полинома, дающего зависимость выходного параметра РЭУ от первичных параметров.
3.3.2 Общие сведения о планировании факторного эксперимента и его применении при функциональных испытаниях
При эксплуатации радиоэлектронного устройства непрерывно меняется его состояние, характеризуемое совокупностью выходных параметров и первичных параметров. При этом важно поддерживать работоспособное состояние (работоспособность), то есть состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской (проектной) документации [15]. Обычно параметры, численные значения которых определяют, в конечном счёте, работоспособность объекта, называют выходными параметрами. Параметры, численные значения которых влияют на значения выходных параметров, называют первичными параметрами. Для усилителя электрических сигналов, например, одним из выходных параметров может быть величина амплитуды выходного напряжения, а первичными параметрами – амплитуда входного напряжения, величина напряжения питания,температура окружающей среды, численные значенияпараметров элементов (резисторов, конденсаторов, транзисторов и т.д.). Изменение состояния РЭУ при эксплуатации из-за изменения параметров элементов происходит непрерывно под действием процессов старения, а также при появлении дефектов, повреждений и отказов. Изменение состояния РЭУ из-за условий эксплуатации происходит при изменении температуры, напряжения питания и величин напряжения входных сигналов и т.д. В инженерной практике часто встречаются случаи, когда трудно получить математическую модель в виде аналитической зависимости выходного параметра от значений первичных параметров (значений параметров элементов, температуры, напряжений и т.д.). Особенно нелегко получить математическую модель для сложных устройств; устройств, содержащих нелинейные элементы; устройств, принцип работы которых недостаточно изучен. В этом случае устройство удобно представить как «чёрный ящик» (рисунок 3.11), преобразующий входные параметры (х 1, х 2, …, хi, …, хn) в выходной параметр у. Зависимости выходного параметра от значений первичных параметров определяют экспериментально.
Рисунок 3.11 – Представление РЭУ в виде «чёрного ящика»
К экспериментам, предназначенным для получения математической регрессионной (полиномиальной) модели, дающей зависимость выходного параметра РЭУ от первичных параметров, относятся: полный факторный активный эксперимент, дробный факторный эксперимент (ДФЭ) и т.п. Смысл этих экспериментов состоит в том, чтобы получить разложение неизвестной функции в ряд Тейлора экспериментальным методом. При этом п
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.17 (0.01 с.) |

 ;
;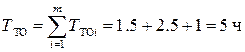 ;
; .
.
 ;
; ;
; ;
; ;
; ;
; .
. ;
;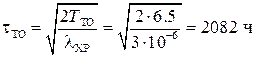 ;
; ;
; .
. ;
; ,
,








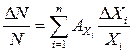 , (3.6)
, (3.6)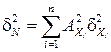 . (3.7)
. (3.7)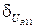 и рассчитать величину
и рассчитать величину 



