
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения об открытой многоканальной смо смешанного типа с ограничением по длине очередиСодержание книги
Поиск на нашем сайте
Для такой СМО (рисунок 4.6) заявка, заставшая все п каналов занятыми, становится в очередь, только если в ней находится менее т заявок; если же число заявок в очереди равно т (больше т оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему не обслуженной. Остальные допущения – о простейшем потоке заявок и о показательном распределении времени обслуживания – оставим прежними.
Рисунок 4.6 – Граф переходов многоканальной СМО смешанного типа с ограничением по длине очереди, изображённый в виде схемы гибели и размножения В данном случае число состояний системы будет конечно, так как общее число заявок, связанных с системой, не может превышать (п + т)(п обслуживаемых и т стоящих в очереди). Расчёт проводим по методике, изложенной в пункте 4.2.3 для открытой одноканальной СМО с ожиданием. Не останавливаясь на этом решении, приведем только окончательные формулы для определения вероятностей Pk состояний k, когда очередь отсутствует, и вероятностей Pn + s состояний (n + s), когда имеется очередь [32].
Вероятность того, что заявка покинет систему необслуженной (формула (4.40)), равна вероятности Рп + т того, что в очереди уже стоят т заявок. Относительная пропускная способность системы: q = 1 – Рп + т . (4.41) Абсолютная пропускная способность: М = λ× q. (4.42) Средняя доля времени, которое система будет простаивать, равна вероятности Р 0(формула (4.34)). Характеристики открытой многоканальной СМО с отказами можно определить по формуле (4.39) при т = 0 и формулам (4.41), (4.42).
4.2.6 Индивидуальные задания для расчета в лабораторной работе характеристик технического обслуживания открытых многоканальных СМО с ожиданием и с отказами
Задание 1 Дана открытая система массового обслуживания смешанного типа с ограниченным ожиданием, имеющая п каналов обслуживания. Интенсивность потока заявок на обслуживание, поступающих в СМО, равна λ [ч-1]. Интенсивность выполнения заявок (интенсивность восстановления) равна μ [ч-1], а отношение λ/μ < п. Значения п, λ [ч-1], μ [ч-1] и ν [ч-1] приведены в таблице 4.2 и зависят от номера варианта, представляющего трёхзначное число. Определить следующие статистические характеристики СМО для трёх значений средней длительности ожидания Т ОЖ: когда 0 < Т ОЖ = 1/ ν < ∞; когда Т ОЖ = 0 (чистая СМО с отказами) и когда Т ОЖ = ∞ (чистая СМО с ожиданием): - вероятность Р 0 простоя СМО из-за отсутствия заявок на обслуживание; - вероятность наличия очереди на обслуживание - среднее число - среднее число заявок N ОЖ, находящихся в очереди на обслуживание; - абсолютную пропускную способность; - относительную пропускную способность. Расчёты провести с использованием программного комплекса MathCAD.
Таблица 4.2 – Численные значения исходных величин для расчёта индивидуального задания №1 с использованием программного комплекса MathCAD
Задание 2 Дана открытая система массового обслуживания смешанного типа с ограничением по длине очереди. Число каналов СМО п, максимальное число заявок в очереди т, поток заявок простейший, время обслуживания распределено по показательному закону. Интенсивность потока заявок λ [ч-1], а средняя длительность обслуживания заявок Т ОБС. Значения λ [ч-1], Т ОБС [ч], п и т приведены в таблице 4.3 и зависят от номера варианта, представляющего трёхзначное число. Определить следующие статистические характеристики СМО для случая, когда все каналы обслуживания исправно работают и для случая, когда один из каналов не работает: - вероятность Р 0 простоя СМО из-за отсутствия заявок на обслуживание; - вероятность того, что заявка покинет систему необслуженной; - абсолютную пропускную способность; - относительную пропускную способность. Определить эти же характеристики, но для открытой многоканальной СМО с отказами (при т = 0). Расчёты провести с использованием программного комплекса MathCAD.
Таблица 4.3 – Численные значения исходных величин для расчёта индивидуального задания №2 с использованием программного комплекса MathCAD
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.128.17 (0.007 с.) |


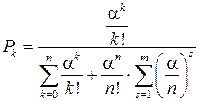 ; 0 £ k £ n; (4.39)
; 0 £ k £ n; (4.39) ; 1 £ s £ m. (4.40)
; 1 £ s £ m. (4.40) ;
;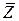 занятых каналов;
занятых каналов;


