Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При анализе переходных процессовСодержание книги
Поиск на нашем сайте
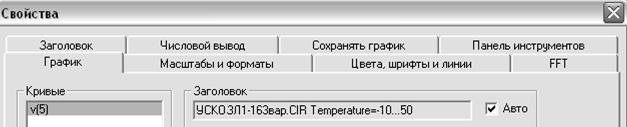
Задаём: - диапазон времени 4m (4 миллисекунды); вывод расчётов Normal; - максимальный шаг по времени 0.0001; начальные условия Zero (нулевые); - количество точек 51; Ö Расчёт по постоянному току; - температура List - 10, +50; Ö Автомасштаб; - квадрат первый слева: масштаб по оси Х – линейный; - квадрат второй слева: масштаб по оси Y – линейный; - квадрат третий слева: цвет линии для графика функции – любой; - квадрат четвертый слева: запись числовых значений по результатам моделирования в текстовом файле – кнопка отжата; - в ячейке P – порядковый номер координатной плоскости для вывода графика функции – номер 1; - в ячейке X Expression определено выражение для оси Х – время T; - в ячейке Y Expression определено выражение для оси Y – значение напряжения в точке 5 схемы (выход усилительного каскада) – v(5); - в ячейках X Range и Y Range определяются диапазоны представления на координатной плоскости значений аргумента и функции, соответственно. Однако, поскольку в нашем случае активирована опция Ö Автомасштаб, то значения ячеек X Range и Y Range системой MicroCAP 8 игнорируются. Для запуска моделирования переходных процессов необходимо нажать кнопку Запуск. В результате на экране появится окно с двумя графиками зависимости выходного напряжения (в точке 5) усилительного каскададля значений температуры окружающей среды -10оС и +50оС при V 1 = 22В, R 4 = 40 Ом (рисунок 3.18).
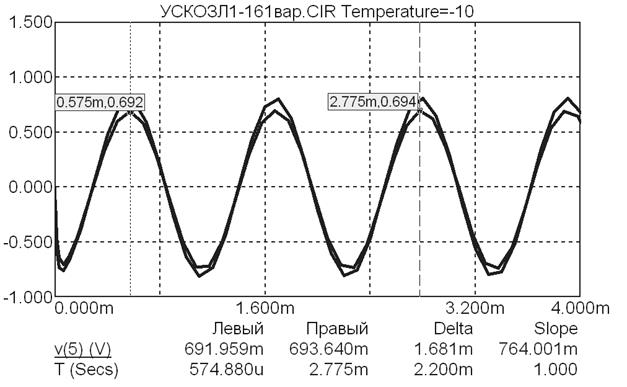
температура окружающей среды -10оС ( V 1 = 22В ( Рисунок 3.18 – Графики зависимости выходного напряжения (точка 5) усилительного каскада Выполним двойной щелчок на заголовке графиков УСКОЗЛ1-163.CIR Temperature=-10…50. В результате появляется диалоговое окно задания параметров оформления графиков Свойства (рисунок 3.19). В этом диалоговом окне можно сделать настройки, которые повышают удобство работы с графиками и помогают в последующем оформлении отчета. Выберем в диалоговом окне Свойства вкладку Цвета, шрифты, линии. На этой вкладке представлен список Объекты (рисунок 3.20). Редактирование типов, размеров и цветов элементов рисунка осуществляется при выборе соответствующего пункта из списка Объекты, например: - редактирование типа, цвета и высоты шрифта текста; - редактирование элементов координатной сетки; - редактирование типа, цвета и высоты шрифта для меток на графике;
- редактирование толщины и цвета кривой и т.д.
Рисунок 3.19 – Верхняя часть диалогового окно Свойства
Рисунок 3.20 – Вкладка Цвета, шрифты и линии диалогового окна Свойства
Схемы и графики, полученные в системе MicroCAP 8, можно передавать во внешние приложения с помощью команды Редактирование / Копировать в буфер обмена / Копировать видимую область в BMP формат. При этом графический образ копируется в буфер обмена Windows. Затем при помощи команды Правка / Вставить любого внешнего приложения, например текстового редактора Microsoft Word, скопированный графический образ размещается в требуемом месте. Для снятия численных значений амплитуды с графиков зависимости выходного напряжения (точка 5) усилительного каскада следует воспользоваться режимом «электронного курсора». Для этого, находясь в окне отображения графиков зависимостей, следует нажать на пиктограмму
температура окружающей среды -10оС ( V 1 = 22В ( с графиком, соответствующим температуре среды -10оС Рисунок 3.21 – Реализация опыта №1 ПФЭ
Из рисунка 3.21 видно, что значения амплитуды выходного напряжения при температуре -10оС составляют 460 мВ и 465 мВ. Более точные значения текущих координат электронного курсора отображаются под координатной плоскостью в столбцах Левый и Правый (первая строка): 459.990 мВ и 465.007 мВ. Для перехода к измерению другой зависимости – выходного напряжения при температуре среды +50 оС – необходимо с помощью клавишей-стрелок или ¯ переместить электронные курсоры на соседний график (рисунок 3.22). Из рисунка 3.22 видно, что значения амплитуды выходного напряжения при температуре +50оС составляют 742.054 мВ и 748.991 мВ.
температура окружающей среды -10оС ( V 1 = 22В ( с графиком, соответствующим температуре среды +50оС
Рисунок 3.22 – Реализация опыта №2 ПФЭ
Подготавливаем в системе MicroCAP 8 схему, изображённую на рисунке 3.15, задав значения V 1 = 22В, R 4 = 80 Ом (
температура окружающей среды -10оСи +50оС при V 1 = 22В ( R 4 = 80 Ом ( соответствующим температуре среды -10оС ( Рисунок 3.23 – Реализация опыта №5 ПФЭ
температура окружающей среды -10оСи +50оС при V 1 = 22В ( R 4 = 80 Ом ( соответствующим температуре среды +50оС ( Рисунок 3.24 – Реализация опыта №6 ПФЭ Подготавливаем в системе MicroCAP 8 схему, изображённую на рисунке 3.15, задав значения V 1 = 24В, R 4 = 40 Ом (
температура окружающей среды -10оСи +50оС при V 1 = 24В ( R 4 = 40 Ом ( соответствующим температуре среды -10оС ( Рисунок 3.25 – Реализация опыта №3 ПФЭ Подготавливаем в системе MicroCAP 8 схему, изображённую на рисунке 3.15, задав значения V 1 = 24В, R 4 = 80 Ом ( Полученные в результате анализа переходных процессов численные значения выходного напряжения ym g = V 5γ для различных сочетаний нормированных переменных
температура окружающей среды -10оСи +50оС при V 1 = 24В ( R 4 = 40 Ом ( соответствующим температуре среды +50оС ( Рисунок 3.26 – Реализация опыта №4 ПФЭ
температура окружающей среды -10оСи +50оС при V 1 = 24В ( R 4 = 80 Ом ( соответствующим температуре среды -10оС ( Рисунок 3.27 – Реализация опыта №7 ПФЭ
температура окружающей среды -10оСи +50оС при V 1 = 24В ( R 4 = 80 Ом ( соответствующим температуре среды +50оС ( Рисунок 3.28 – Реализация опыта №8 ПФЭ
Таблица 3.5 – Матрица планирования ПФЭ 2 п для п = 3 и γ = 2 (ПФЭ 23)
Среднее значение т (ут) в каждой т -ой строке в таблице 3.5 вычислено по формуле (3.22):
Для вычисления коэффициентов полинома (3.12):
используются выражения (3.16), в которых следует принять N = 8, а величины ут – равными средним измеренным значениям т (ут), взятым из таблицы 3.5 (ут = т (ут)). Тогда:
Если пренебречь квадратичными членами, то полином (3.12) для нашего примера примет вид:
Перейдём от коэффициентов В, которые получаются из опыта, к коэффициентам β в натуральном масштабе в полиноме (3.8). При использовании полиномов первого порядка расчёт проводим по формулам (3.15):
Полином первого порядка с коэффициентами β в натуральном масштабе для нашего примера примет вид: V 5 = (-1325.193 + 3.551· Т + 77.378· V 1 + 3.716· R 4) мВ. Значения строчной дисперсии вычислены по формуле (3.23), которая при γ = 2 примет вид:
D (y 1) = (459.99 – 462.499)2 +(465.007 – 462.499)2 = 12.585мВ2; D (y 2) = (742.054 – 745.523)2 + (748.991 – 745.523)2 = 24.061 мВ2; D (y 3) = (691.959 – 692.799)2 + (693.64 – 692.799)2 = 1.413 мВ2; D (y 4) = (791.565 – 795.791)2 + (800.017 – 795.791)2 = 35.718 мВ2; D (y 5) = (565.848 – 566.293)2 + (566.739 – 566.293)2 = 0.397 мВ2; D (y 6) = (908.283 – 910.034)2 + (911.786 – 910.034)2 = 6.136мВ2; D (y 7) = (846.627 – 846.138)2 + (845.649 – 846.138)2 = 0.478 мВ2; D (y 8) = (961.79 – 968.646)2 + (975.502 – 968.646)2 = 94.009 мВ2. Исходя из строчной дисперсии, по формуле (3.24) находим дисперсию воспроизводимости:
Зная дисперсию воспроизводимости, находим дисперсию полиномиальных коэффициентов Bi:
По формуле (3.30) вычисляем среднее квадратическое отклонение коэффициентов: σ(Bi) = [ D (Bi)]0.5 = 2.7310.5= 1.653мВ. Значения коэффициентов уравнения (3.12б) существенно больше. Следовательно, можно полагать, что все оставшиеся коэффициенты полинома значимы. Дополнительно производим проверку значимости с использованием критерия Стьюдента. Для уровня значимости, равного a = 0.05 и степеней свободы М = (N ·γ – N) = 8 · 2 – 8 = 8, из таблицы 3.3 находим t ТАБЛ(УЗ) = 2.306. Тогда:
Полученное число 3.811 меньше коэффициентов Bi полинома (3.12б): B 0 = 748.465 мВ; B 1 = 106.533 мВ; B 2 = 77.378 мВ; B 3 = 74.313 мВ. Это согласно (3.28) является подтверждением того, что все коэффициенты полинома значимы. Производим проверку адекватности путём сравнения результатов эксперимента т (ут g) для разных сочетаний переменных
Таблица 3.6 – Сравнение результатов эксперимента т (ут g) с результатами, которые получены после расчета по полиному
Приведём результаты расчета выходного параметра ут РАСЧ по этому полиному с нормированными переменными:
Затем по формуле (3.31) вычисляем дисперсию адекватности:
где т (ут g) – среднее значение результата эксперимента, взятое из т -ой строки таблицы 3.5; ут РАСЧ – результаты расчета по полиному (3.12б) для того же сочетания переменных; d – количество членов, оставленных в полиноме. Для D АД(y)принимается (N – d) степеней свободы, а для D B(у)берется N ·(γ – 1) степеней свободы. Для проверки адекватности по формуле (3.32) вычисляем случайную величину F АД распределения Фишера:
Адекватность полинома установим с помощью таблицы 3.4 распределения Фишера при сравнении величины F АДс F ТАБЛ. Если F АД< F ТАБЛ, то принимается решение об адекватности полинома результатам опыта. В противном случае принимается решение о его неадекватности. Для рассматриваемого примера: - количество членов, оставленных в полиноме d = 4; - количество степеней свободы для дисперсии адекватности: (N – d) = 8 – 4 = 4, т.е. М ′ = 4; - количество степеней свободы для дисперсии воспроизводимости: N ·(γ – 1) = 8·(2 – 1) = 8, т.е. М = 8; - из таблицы 3.4 при уровне значимости a = 0.05 с учетом того, что М = 8, a М ′ = 4, получаем F ТАБЛ = 6.04, а при уровне значимости a = 0.01 F ТАБЛ = 14.8. Как видно, F АД = 246.714 > F ТАБЛ = 6.04 при уровне значимости a = 0.05 и F АД = 246.714 > F ТАБЛ = 14.8 при уровне значимости a = 0.01. Следовательно, в отличие от предыдущей задачи полученный линейный полином не адекватен результатам опыта с вероятностью ошибки в этом решении не меньше, чем 1 –a = 0.99. Для обеспечения адекватности в полином следует ввести коэффициенты взаимодействия. В рассматриваемом примере можно вычислить коэффициенты взаимодействия Bij 2-го порядка [20]:
и получить неполный полином 2-го порядка. Как упоминалось ранее, получение коэффициентов при Для вычисления коэффициентов взаимодействия 2-го порядка заполним вспомогательную таблицу 3.7, а затем запишем неполный полином 2-го порядка:
С помощью вспомогательной таблицы 3.8 вычислим относительные отклонения измеренных значений от расчётных (δ%) при использовании линейного полинома и от расчётных значений при использовании неполного полинома 2-го порядка (δ% УТОЧ). Эти отклонения рассчитаем по формулам:
и
где
По данным таблицы 3.8 видно уменьшение относительных отклонений измеренных значений от расчётных при использовании полинома 2-го порядка (δ%УТОЧ < δ%). Таблица 3.7 – Вспомогательная таблица для вычисления коэффициентов взаимодействия 2-го порядка
Таблица 3.8 – Вспомогательная таблица для вычисления относительных отклонений измеренных значений от расчётных
Вычислим коэффициенты взаимодействия 2-го порядка b ij в натуральном масштабе:
В двух последних формулах шаг изменения температуры окружающей среды Δ х 1 = Δ Т = ±30оС, шаг изменения напряжения питания Δ х 2 = Δ V 1 = ±1В, шаг изменения сопротивления нагрузки Δ х 3 = Δ R 4 = ±20 Ом. Неполный полином 2-го порядка с коэффициентами βв натуральном масштабе для нашего примера примет вид:
Для анализа точности и стабильности выходного параметра вычислим по формуле (3.21) коэффициенты ki ОТН в уравнении отклонений:
и коэффициенты взаимодействия в уравнении отклонений
гденоминальная величина: у 0 = V5 0 = (829.269 + 828.989)/2 = 829.129 мВ это значение выходного параметра V5, определённое из графика (рисунок 3.29) для номинальных значений исходных параметров: температуры окружающей среды 20оС (х 1,0), напряжения питания V 10 = 23В(х 2,0) и R 40 = 60 Ом(х 3,0).
Получим явный вид уравнения отклонений неполного полинома 2-го порядка:
Подставим численные значения величин коэффициентов ki ОТН и kij ОТН:
температура окружающей среды 20оС(х 1,0), напряжение питания V 10 = 23В(х 2,0) и R 40 = 60 Ом (х 3,0) Рисунок 3.29 – График зависимости выходного напряжения усилительного каскададля номинальных значений
3.3.5 Лабораторное задание
Получить у преподавателя номер варианта задания. Для выходного напряжения у усилительного каскада, математическая модель которого получена в системе MicroCAP 8, требуется получить полиноминальную модель с помощью ПФЭ 2 п для п = 3 (ПФЭ 23) с вычислением коэффициентов 1-го порядка, а также провестистатистический анализ полинома и качества эксперимента с проверкой значимости членов полинома и адекватности этого полинома результатам опыта. При неадекватности полинома 1-го порядка результатам опыта получить полиноминальную модель с вычислением коэффициентов взаимодействия 2-го порядка. Для вариантов с 1 по 6 и с 13 по 18 исследуется схема, изображённая на рисунке 3.15, а для вариантов с 7 по 12 и с 19 по 24 – схема, изображённая на рисунке 3.30. Для схемы на рисунке 3.15 выходной параметр – это напряжение резисторе R 4, а для схемы на рисунке 3.30 выходным параметром следует считать напряжение на коллекторе транзисторе. Заметим, что номер узла для измерения выходного напряжения в каждом конкретном случае может быть иным, отличным от номеров, показанных на рисунках 3.15 и 3.30.
Рисунок 3.30 – Усилительный каскад с комбинированным управлением по задающему воздействию (напряжению базы транзистора)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.35.247 (0.013 с.) |


 )и +50оС (
)и +50оС ( );
); ); R 4 = 40 Ом (
); R 4 = 40 Ом ( )
)

 (на рисунке 3.18 третья слева на панели инструментов). После этого на экране появляются изображения двух электронных курсоров, совмещенных с одним из графиков – выходным напряжением усилителя при температуре среды -10оС(рисунок 3.21). Заметим, что электронные курсоры можно произвольно перемещать вдоль всего графика функции с помощью мыши или с помощью клавишей-стрелок и ®. Перемещение правого электронного курсора на экране происходит либо при нажатой правой клавиши мыши, либо при нажатой клавише Shift (в случае перемещения с помощью стрелок). Для нахождения локальных максимумов функции можно воспользоваться пиктограммой
(на рисунке 3.18 третья слева на панели инструментов). После этого на экране появляются изображения двух электронных курсоров, совмещенных с одним из графиков – выходным напряжением усилителя при температуре среды -10оС(рисунок 3.21). Заметим, что электронные курсоры можно произвольно перемещать вдоль всего графика функции с помощью мыши или с помощью клавишей-стрелок и ®. Перемещение правого электронного курсора на экране происходит либо при нажатой правой клавиши мыши, либо при нажатой клавише Shift (в случае перемещения с помощью стрелок). Для нахождения локальных максимумов функции можно воспользоваться пиктограммой  , расположенной на панели инструментов. При нажатии на эту пиктограмму левый электронный курсор перемещается на ближайший локальный максимум функции. Для того чтобы задействовать для поиска максимумов правый электронный курсор, необходимо его сначала активировать. Делается это правой кнопкой мыши; затем, также как и в предыдущем случае, нажатие на пиктограмму
, расположенной на панели инструментов. При нажатии на эту пиктограмму левый электронный курсор перемещается на ближайший локальный максимум функции. Для того чтобы задействовать для поиска максимумов правый электронный курсор, необходимо его сначала активировать. Делается это правой кнопкой мыши; затем, также как и в предыдущем случае, нажатие на пиктограмму 

 ). В этом случае при температуре окружающей среды -10оС (
). В этом случае при температуре окружающей среды -10оС (

 ,
, 
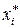 (рисунки 3.21 – 3.28) заносим в матрицу планирования ПФЭ 2 п для п = 3 и числа измерений γ = 2 (таблица 3.5).
(рисунки 3.21 – 3.28) заносим в матрицу планирования ПФЭ 2 п для п = 3 и числа измерений γ = 2 (таблица 3.5).




 -1
-1
 .
.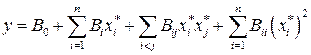


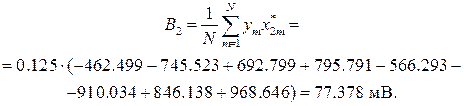

 . (3.12б)
. (3.12б)
 ;
; ;
;  ;
; .
.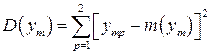 .
.
 .
. .
. с теми результатами, которые при том же сочетании переменных получены для параметра после расчета по полиному (3.12б). Результаты расчета помещаем в таблицу 3.6.
с теми результатами, которые при том же сочетании переменных получены для параметра после расчета по полиному (3.12б). Результаты расчета помещаем в таблицу 3.6. ,
,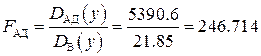 .
. (3.18)
(3.18)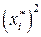 из результатов ПФЭ в нашем случае невозможно.
из результатов ПФЭ в нашем случае невозможно.
 (3.33)
(3.33)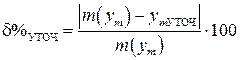 , (3.34)
, (3.34) . (3.35)
. (3.35)
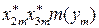

 =
=
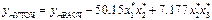
 ; (3.36)
; (3.36) ;
; .
.

 , (3.37)
, (3.37) ;
; ;
; ;
; ;
;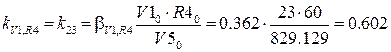 .
. . (3.38)
. (3.38)