
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многоканальной смо с ожиданиемСодержание книги
Поиск на нашем сайте
Под термином техническоесостояние Еk понимают совокупность подверженных изменению в процессе производства или эксплуатации свойств объекта, характеризуемую в определённый момент признаками, установленными технической документацией. На рисунке 4.1 введены следующие обозначения: - Еk – техническоесостояние СМО, при котором k из n работающих приборов находятся в состоянии неработоспособности; - r − число каналов обслуживания; - λ [ч-1] − интенсивность поступления заявок, равная интенсивности отказов одного прибора; - μ [ч-1] − интенсивность обслуживания (восстановления или ремонта) в одном канале. Указанная СМО может использоваться как система технического обслуживания не только приборов, но и транспорта (парки самолетов, автомобилей и т.п.). Академик А.Н.Колмогоров сформулировал инженерное правило составления дифференциальных уравнений по виду графа или по виду схемы состояний [1, 4]: «Производная от вероятности пребывания системы в любой момент времени в состоянии k равна алгебраической сумме произведений интенсивностей переходов в k -ое состояние (или из k -ого состояния) на вероятность того состояния, откуда совершается переход в k- ое состояние. Причем, тем слагаемым, которым соответствуют уходящие стрелки из k -ого состояния, приписывается знак «минус», а входящим – «плюс». Анализ графа (рисунок 4.1) позволяет вывести дифференциальное уравнение для вероятностей состояний:
Для установившегося режима (n – k + 1)×λ× Pk -1 + [(n – k)×λ + k ×μ]× Pk + (k + 1)×μ× Pk +1 = 0. (4.4) Решение уравнения для вероятностей в этом случае дает результат: Pk = Ak × P 0, (4.5) где P 0 − вероятность того, что работают все приборы.
Для проверки правильности расчета Pk используется нормировочное отношение:
Суммарная погрешность расчета Pk находится из выражения:
Полученные выражения для Pk (вероятностей пребывание системы в состоянии k) позволяют с помощью схемы для определения статических характеристик СМО, изображенной на рисунке 4.2, определять эти характеристики [1]:
Рисунок 4.2 – Схема определения статических характеристик СМО
а) среднее количество заявок в каналах обслуживания, то есть среднее количество каналов занятых на ремонте:
где первое слагаемое характеризует отсутствие очереди, а второе – очередь; б) пропускная способность:
где Т В− среднее время восстановления одного прибора, величина обратная интенсивности восстановления; в) среднее число заявок, находящихся в СМО (как в каналах обслуживания, так и в очереди на обслуживание):
г) среднее число заявок, находящихся в очереди на обслуживание:
д) среднее число простаивающих каналов обслуживания из-за отсутствия заявок:
е) среднее относительное время простоя каждого канала СМО из-за отсутствия заявок:
ж) среднее относительное значение времени пребывания заявок в очереди на обслуживание:
з) среднее относительное значение времени пребывание заявок в очереди и в канале обслуживания:
и) при определении минимального количества каналов обслуживания r min, обеспечивающего отсутствие очереди на обслуживание, используют неравенство:
где К П и К Г – коэффициенты простоя и готовности, соответственно.
Пример использования ТМО для расчета характеристик технического обслуживания замкнутой многоканальной СМО с ожиданием
Дана СМО, состоящая из n = 9 работающих приборов и r = 3 каналов обслуживания. Интенсивность поступления заявок, равная интенсивности отказов одного прибора, λ = 0.1671 [ч-1], а интенсивность обслуживания (восстановления или ремонта) в одном канале μ = 0.3 [ч-1]. Требуется определить: а) среднее количество заявок б) пропускную способность M; в) среднее число заявок K, находящихся в СМО (как в каналах обслуживания, так и стоящих в очереди на обслуживание); г) среднее число заявок N ОЖ, находящихся в очереди на обслуживание; д) среднее число простаивающих каналов обслуживания из-за отсутствия заявок R ПР; е) среднее относительное время простоя каждого канала обслуживания из-за отсутствия заявок Т ПР; ж) среднее относительное значение времени пребывания заявки в очереди на обслуживание Т ОЖ; з) среднее относительное значение времени пребывания заявки в очереди и в канале обслуживания Т ОБС; и) потребное количество каналов, обеспечивающее отсутствие очереди r ОПТ. Решение: а) находим вспомогательные коэффициенты Ак при 1 £ k £ n:
А 1 = 7.52; А 2 = 11.169; А 3 = 14.516; А 4 = 16.171; А 5 = 15.012; А 6 = 11.149; А 7 = 6.21; А 8 = 2.306; А 9 = 0.428; б) определим вспомогательную величину Р 0 (вероятность того, что в системе исправно работают все приборы):
в) находим вероятность нахождения системы в k -ом состоянии, т.е. в состоянии, когда k приборов отказали (1 £ k £ n): Pk = Ak × P 0; P 1 = 0.088; P 2 = 0.131; P 3 = 0.17; P 4 = 0.189; P 5 = 0.176; P 6 = 0.13; P 7 = 0.073; P 8 = 0.027; P 9 = 5.009·10-3. Проверка правильности решения:
г) находим среднее количество заявок в каналах обслуживания:
д) находим пропускную способность M:
е) находим среднее количество заявок находящихся в СМО (в каналах и в очереди):
ж) находим среднее количество заявок, находящихся в очереди на обслуживание:
з) находим среднее количество простаивающих каналов из-за отсутствия заявок:
и) находим среднее относительное время простоя из-за отсутствия заявок:
к) находим среднее относительное значение времени пребывания заявки в очереди:
л) находим среднее относительное значение времени пребывания заявки в СМО:
м) определяем коэффициент готовности:
н) находим потребное количество каналов, необходимых для обеспечения отсутствия очереди:
Принимаем r ОПТ= 4, то есть равным ближайшему целому числу большему 3.22.
4.1.4 Индивидуальные задания для расчета в лабораторной работе характеристик технического обслуживания замкнутой многоканальной СМО с ожиданием
Дана СМО, состоящая из n работающих приборов и r каналов обслуживания. Интенсивность поступления заявок (интенсивность отказов одного прибора) равна λ, а интенсивность обслуживания (восстановления или ремонта) в одном канале равна μ. Определить: а) среднее количество заявок б) пропускную способность M; в) среднее число заявок K, находящихся в СМО (как в каналах обслуживания, так и стоящих в очереди на обслуживание); г) среднее число заявок N ОЖ, находящихся в очереди на обслуживание; д) среднее число простаивающих каналов обслуживания из-за отсутствия заявок R ПР; е) среднее относительное время простоя каждого канала обслуживания из-за отсутствия заявок Т ПР; ж) среднее относительное значение времени пребывания заявки в очереди на обслуживание Т ОЖ; з) среднее относительное значение времени пребывания заявки в очереди и в канале обслуживания Т ОБС; и) потребное количество каналов, обеспечивающее отсутствие очереди r ОПТ. Численные значения исходных величин для расчёта индивидуальных заданий даны в таблице 4.1 и зависит от номера варианта.
Таблица 4.1 – Численные значения исходных величин для расчёта индивидуальных заданий с использованием программного комплекса MathCAD
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

 . (4.3)
. (4.3) , так как Pk в этом случае не меняется во времени, и уравнение для вероятности состояний примет вид:
, так как Pk в этом случае не меняется во времени, и уравнение для вероятности состояний примет вид: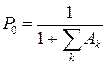 ; (4.6)
; (4.6) . (4.7)
. (4.7) . (4.8)
. (4.8) . (4.9)
. (4.9)

 , (4.10)
, (4.10)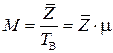 , (4.11)
, (4.11)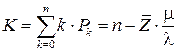 ; (4.12)
; (4.12) ; (4.13)
; (4.13) ; (4.14)
; (4.14) при r > 1; (4.15)
при r > 1; (4.15) ; (4.16)
; (4.16)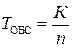 ; (4.17)
; (4.17) , (4.18)
, (4.18) , занятых в каналах обслуживания, то есть занятых каналов на ремонте;
, занятых в каналах обслуживания, то есть занятых каналов на ремонте; ;
;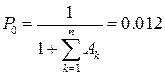 ;
;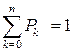 ;
; ;
; 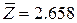 ;
; ; M = 0.797;
; M = 0.797; ; K = 4.227;
; K = 4.227; ; N ОЖ = 1.569;
; N ОЖ = 1.569; ; R ПР = 0.343;
; R ПР = 0.343;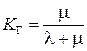 ; К Г = 0.642;
; К Г = 0.642; ; r ОПТ ³ 3.22.
; r ОПТ ³ 3.22. , занятых в каналах обслуживания, то есть занятых каналов на ремонте;
, занятых в каналах обслуживания, то есть занятых каналов на ремонте;



