
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистических гипотез с помощью доверительных интерваловСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Доверительные интервалы можно использовать для оценки статистической значимости различий. Если 100(1 – α)-процентный доверительный интервал разности средних не содержит нуля, то различия статистически значимы; напротив, если этот интервал содержит ноль, то различия статистически не значимы.
27. Оценка эффектов уровней фактора Следующим шагом дисперсионного анализа является выяснение того, в какой мере параметры μj отличаются друг от друга, т. е. какие именно из средних μj не равны. Для проверки нескольких гипотез о равенстве математических ожиданий используют методы множественного сравнения. Одним из таких методов является метод множественных сравнений Шеффе, который позволяет проверять гипотезы для любых комбинаций средних (математических ожиданий).
коэффициенты которой удовлетворяют условию:
Примерами контрастов являются
При использовании методов множественного сравнения для проверки гипотез можно столкнуться с противоречием когда две величины, порознь равные третьей, окажутся не равны между собой. Чтобы избежать этого, сравнения необходимо проводить в определенном порядке. А именно, следует сравнить группу с наибольшим средним с группой, имеющей наименьшее среднее, затем с группой с наименьшим средним среди остальных групп и т. д. Когда при сравнении обнаружится, что μj и μt различаются незначимо или не останется группы с меньшим выборочным средним, следует заменить группу с наибольшим средним на группу со вторым по величине средним и начать процедуру сначала.
28. Двухфакторный дисперсионный анализ с пересечением уровней Пусть на исследуемую величину могут оказывать влияние два фактора A и B, каждый из которых имеет конечное число уровней. При этом ставится вопрос, как влияют и влияют ли вообще эти факторы на исследуемую величину. Здесь уже необходимо уделить внимание способу взаимосвязи факторов. Для большинства практических задач достаточно ограничиться двумя способами: пересечением и группировкой. Два фактора A и B называются пересекающимися, если в плане эксперимента предусмотрены все возможные сочетания факторов. Фактор B группируется фактором A, если каждый уровень фактора B сочетается не более, чем с одним уровнем фактора A. Пусть xijt обозначает значение наблюдения полученное при t -м повторении эксперимента в ячейке ij, i = 1,..., k; j = 1,... n; t = 1,... m. Модель дисперсионного анализа представим в виде:
здесь μ – генеральное среднее, α i – дифференциальный эффект фактора A, βj – дифференциальный эффект фактора B. Величина (αβ) ij – называется взаимодействием i -го уровня фактора A и j -го уровня фактора B. Проверяемыми гипотезами являются:
Как и в однофакторном дисперсионном анализе проверка этих гипотез основывается на сравнении двух независимых оценок дисперсии σ 2. При этом одна из оценок действует в независимости от того, верна ли гипотеза H0, а вторая – только в случае справедливости этой гипотезы.
Входящую в оценку дисперсии генеральной совокупности сумму квадратов можно представить в виде суммы четырех отдельных сумм квадратов СКA, СКB, СКAB, СК0:
Xарактеризует эффект взаимодействия факторов:
Oстаточная сумма квадратов
Гипотеза H0: β1 = β2 =... = βn = 0 проверяется с помощью отношения
Результаты дисперсионного анализа представляют следующей таблицей
29. Двухфакторный дисперсионный анализ с группировкой уровней Пусть на исследуемую величину могут оказывать влияние два фактора A и B, каждый из которых имеет конечное число уровней. При этом ставится вопрос, как влияют и влияют ли вообще эти факторы на исследуемую величину. Здесь уже необходимо уделить внимание способу взаимосвязи факторов. Для большинства практических задач достаточно ограничиться двумя способами: пересечением и группировкой. Два фактора A и B называются пересекающимися, если в плане эксперимента предусмотрены все возможные сочетания факторов. Фактор B группируется фактором A, если каждый уровень фактора B сочетается не более, чем с одним уровнем фактора A.
Здесь µ – генеральное среднее, αi – дифференциальный эффект, определяемый i -м уровнем фактора A, величины bj (i) независимы и распределены по нормальному закону с нулевым средним и дисперсией σ 2 b (a), εijt – остаточные случайные величины Результаты дисперсионного анализа оформляются в виде следующей таблицы
Статистики для проверки гипотез имеют вид:
для гипотезы H0: все αi = 0;
для гипотезы H0: σb ( a ) = 0;
30. Проверка однородности дисперсий
может понадобиться проверить, изменяется ли D[ ε ij] = σi 2 в различных группах, т. е. проверить гипотезу σ 12 = σ 22 = … = σk 2 Критерий Бартлетта
Бартлетт доказал, что, если справедлива нулевая гипотеза, то статистика
при N → ∞ асимптотически имеет распределение χ2 с k −1 степенями свободы. Однако этот критерий слишком чувствителен к отклонению распределений совокупностей от нормальности, поэтому значимость статистики U2 может указывать не на отсутствие однородности дисперсий, а просто на отклонение от нормальности. Критерий Кочрена основан на статистике:
при этом объемы выборок, по которым рассчитаны sj 2, должны быть одинаковы. Распределение этой статистики известно точно и зависит только от числа степеней свободы n−1 и количества выборок. Нулевая гипотеза H0: все σ j2 равны отвергается с уровнем значимости α, если значение статистики G > Gкр. Критическое значение статистики находят по таблицам процентных точек распределения Кочрена.
31. Непараметрические методы факторного анализа. Ранговый однофакторный анализ. В ряде случаев предположение о нормальности закона распределения остаточных случайных величин в моделях, описанных в дисперсионном анализе, не выполняется. Более того, этот закон оказывается неизвестным. Тогда используют различные непараметрические методы проверки однородности нескольких выборок, из которых наиболее разработаны ранговые методы. Обозначив через rij ранг значения xij, который получит это значение при упорядочении всей совокупности данных в порядке возрастания, придем к следующей таблице данных.
В рамках ранговых критериев нулевая гипотеза формулируется как гипотеза о том, что все k выборок (столбцов таблицы) являются выборками из одного и того же распределения. Строго говоря, если нулевая гипотеза отвергается, то можно только утверждать, что распределения совокупностей различны. Это, однако, не означает, что их средние не равны между собой. Для вывода о том, что выборки производились из совокупностей с различными математическими ожиданиями, необходимо предположить, что эти совокупности одинаковы по всем другим параметрам. Критерий Краскела-Уолллиса.
Если между столбцами нет систематических различий, то средние ранги R.j не должны значительно отличаться от среднего ранга, рассчитанного по всей совокупности рангов. Общее число наблюдений N = n 1 + n 2 + … nk. Для объединенной группы рангами являются числа 1, 2,..., N и общая сумма рангов равна:
Тогда средний ранг для объединенной группы равен: Далее найдем величину, аналогичную межгрупповой сумме квадратов отклонений
Величина СКR зависит от размеров групп. Чтобы получить показатель, отражающий их различия, следует поделить СКR на N (N +1)/12. Полученная величина
является значением критерия Краскела-Уолллиса.
где – сумма рангов j -го столбца.
При больших объемах выборок, которые находятся за пределами таблиц, случайная величина H при справедливости нулевой гипотезы приближенно распределена по закону χ2 с k − 1 степенями свободы. Поэтому в этом приближении нулевая гипотеза отвергается на уровне значимости α, если вычисленное по данным значение статистики H больше χ2k−1;α – α процентной точки распределения χ2 с k−1 степенями свободы.
где g – число групп совпадающих наблюдений; Tj = (tj 3 − tj); tj – число совпадающих наблюдений в группе с номером j.
32. Непараметрические методы факторного анализа. Ранговый двухфакторный анализ без повторений В ряде случаев предположение о нормальности закона распределения остаточных случайных величин в моделях, описанных в дисперсионном анализе, не выполняется. Более того, этот закон оказывается неизвестным. Тогда используют различные непараметрические методы проверки однородности нескольких выборок, из которых наиболее разработаны ранговые методы. Обозначив через rij ранг значения xij, который получит это значение при упорядочении всей совокупности данных в порядке возрастания, придем к следующей таблице данных.
В рамках ранговых критериев нулевая гипотеза формулируется как гипотеза о том, что все k выборок (столбцов таблицы) являются выборками из одного и того же распределения. Строго говоря, если нулевая гипотеза отвергается, то можно только утверждать, что распределения совокупностей различны. Это, однако, не означает, что их средние не равны между собой. Для вывода о том, что выборки производились из совокупностей с различными математическими ожиданиями, необходимо предположить, что эти совокупности одинаковы по всем другим параметрам. Критерий Фридмана Рассмотрим двухфакторный эксперимент, когда на уровнях фактора B проведено по одному наблюдению (неповторяемый эксперимент). Его модель имеет вид
В отличие от дисперсионного анализа нам неизвестно распределение случайных величин εij. Известно только, что оно непрерывно, а сами случайные величины независимы в совокупности и имеют одинаковое распределение. В этом случае для оценки влияния на исследуемый признак факторов A и B используется непараметрический критерий Фридмана, который основан на переходе от значений xij в таблице данных двухфакторного анализа к их рангам.
В отличие от однофакторного анализа ранжирование осуществляется не по всей совокупности величин xij, а по строкам (для проверки однородности данных по столбцам таблицы данных), т. е. ранжируется каждая отдельная строка таблицы данных. Обозначим полученные ранги величин xij через rij. Будем считать, что среди элементов xij, стоящих в одной строке таблицы, нет совпадающих. Определим средние значением рангов по i -му столбцу
При справедливости нулевой гипотезы в силу равновероятности всех перестановок рангов в каждой строке значение Ri. для каждого i не должно сильно отличаться от величины R.. = 0.5(k + 1), представляющей собой общий средний ранг всех элементов таблицы рангов.
При вычислениях удобно использовать другую запись статистики:
Для небольших значений k и n имеются таблицы процентных точек распределения статистики Фридмана, позволяющие при заданном уровне значимости α находить критические значения s (k, n, α). При больших n для определения критических значений пользуются аппроксимацией статистики S. При справедливости нулевой гипотезы статистика в этом случае аппроксимируется распределением χ2 с k −1 степенями свободы. Нулевая гипотеза об однородности данных по столбцам (отсутствие влияния фактора A) принимается с уровнем значимости α, если расчетное значение статистики S меньше критического значения и отвергается, если оно больше критического. Если в строках таблицы данных имеются совпадающие значения, при переходе к таблице рангов используются средние ранги, а вместо статистики S используется ее модификация. Для проверки гипотезы об эффектах фактора B (строк) следует поменять местами строки и столбцы таблицы данных.
33. Корреляционный анализ. Постановка задач статистического исследования зависимостей В математическом анализе зависимость между величинами x и y выражается функцией y = f (x), где каждому значению x соответствует одно и только одно значение y. Такая связь называется функциональной. Для случайных величин X и Y такую зависимость можно установить не всегда. Связь между случайными величинами является не функциональной, а случайной (стохастической), при которой изменение переменной X влияет на значения переменной Y через изменение закона распределения случайной величины Y. Таким образом задача корреляционного анализа исследование наличия взаимосвязей между отдельными группами переменных и установление тесноты (силы) связи между ними. Порядок проведения корреляционного анализа как правило включает: ü выбор показателя статистической связи анализируемых переменных ü оценка значения этого показателя по имеющимся экспериментальным данным, т. е. нахождение его точечной и интервальной оценки ü проверка статистической гипотезы о том, что значение показателя статистической связи значимо отличается от нуля
34. Измерители парной статистической связи. Корреляционное отношение
В процессе наблюдения величины Y = ϕ (X) для каждого фиксированного значения x′ случайной величины X можно иметь разброс значений Y, обусловленный погрешностями прибора или какими-либо неконтролируемыми факторами, и можно вычислить величину дисперсии
Тогда суммарная дисперсия случайной величины Y = ϕ (X) будет состоять из двух слагаемых:
которое показывает долю дисперсии, обусловленную чисто функциональной связью ϕ (X), в полной дисперсии случайной величины Y. Это наиболее общая характеристика степени тесноты связи между случайными величинами Y и X. Очевидно, что 0 ≤ ρ 2 yx ≤ 1. Стремление ρ 2 yx к нулю означает, что доля дисперсии, обусловленная функциональной связью, очень мала. Наоборот, стремление ρ 2 yx к единице показывает, что случайными изменениями Y можно пренебречь и вся дисперсия обусловлена функциональной зависимостью Y = ϕ (X). Аналогично определяется квадрат корреляционного отношения ρ 2 xy переменной X по Y. Однако между ρ 2 yx и ρ 2 xy нет какой-либо простой зависимости. Положительный корень из ρ 2 yx носит название корреляционного отношения, которое является показателем статистической связи между двумя случайными величинами X и Y для самой общей ситуации, когда закон распределения системы (X, Y) является произвольным.
35. Коэффициент корреляции как измеритель степени тесноты связи Рассмотрим двумерную нормальную совокупность, плотность вероятности которой имеет вид
где rxy – коэффициент корреляции между случайными величинами Y и X. Для условной плотности вероятности случайной величины Y (плотности при условии, что случайная величина X приняла определенное значение X = x) получим:
Отсюда видно, что условная плотность вероятности случайной величины Y тоже имеет нормальное распределение с математическим ожиданием
и дисперсией
характеризующей разброс случайной величины Y вокруг математического ожидания. Тогда для квадрата корреляционного отношения получаем
т. е. корреляционное отношение для двумерного нормального распределения совпадает с коэффициентом корреляции. Аналогично можно показать, что ρ 2 xy= r 2 yx, откуда, поскольку r 2 xy= r 2 yx, для нормально распределенных величин ρ 2 xy= ρ 2 yx=r 2.
В общем случае показатели ρ 2 xy и r 2 связаны неравенствами При этом возможны следующие варианты: ü r 2 = ρ 2 yx= 1только тогда, когда имеется строгая линейная функциональная зависимость Y от X ü r 2 < ρ 2 yx= 1только тогда, когда имеется строгая нелинейная функциональная зависимость Y от X ü r 2 = ρ 2 yx< 1 только тогда, когда зависимость Y от X строго линейна, но нет функциональной зависимости ü r 2 < ρ 2 yx< 1 указывает на то, что не существует функциональной зависимости, а некоторая нелинейная кривая “подходит” лучше, чем “наилучшая” прямая линия. Таким образом, в качестве показателя статистической связи между двумя случайными количественными переменными X и Y следует выбрать корреляционное отношение ρyx (или ρxy), если закон распределения системы (X, Y) вызывает сомнение. Если же можно с большой степенью уверенности считать закон распределения системы (X, Y) нормальным, то вместо корреляционного отношения следует использовать коэффициент корреляции r.
|
||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.012 с.) |

 Наиболее часто приходится проводить сравнение так называемых контрастов в средних. Контрастом называется линейная комбинация средних вида
Наиболее часто приходится проводить сравнение так называемых контрастов в средних. Контрастом называется линейная комбинация средних вида



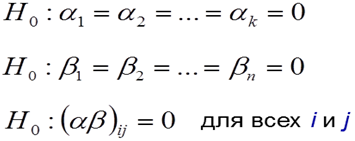
 Рассматривая совокупность данных как одну выборку из генеральной совокупности, получим оценку генерального среднего в виде:
Рассматривая совокупность данных как одну выборку из генеральной совокупности, получим оценку генерального среднего в виде: и несмещенную оценку дисперсии генеральной совокупности:
и несмещенную оценку дисперсии генеральной совокупности: Характеризует разброс наблюдаемых значений между столбцами (уровнями фактора A) таблицы данных:
Характеризует разброс наблюдаемых значений между столбцами (уровнями фактора A) таблицы данных: Xарактеризует разброс наблюдаемых значений между строками (уровнями фактора B) таблицы:
Xарактеризует разброс наблюдаемых значений между строками (уровнями фактора B) таблицы:


 Гипотеза H0: α1 = α2 =... = αk = 0 проверяется с помощью отношения
Гипотеза H0: α1 = α2 =... = αk = 0 проверяется с помощью отношения
 Гипотеза об отсутствии взаимодействия между факторами (гипотеза об аддитивности) проверяется с помощью отношения:
Гипотеза об отсутствии взаимодействия между факторами (гипотеза об аддитивности) проверяется с помощью отношения:
 Фактор B с n уровнями был назван сгруппированным фактором A с k уровнями, если каждый уровень фактора B сочетается не более, чем с одним уровнем фактора A. Двухфакторный анализ с группировкой с описывается моделью:
Фактор B с n уровнями был назван сгруппированным фактором A с k уровнями, если каждый уровень фактора B сочетается не более, чем с одним уровнем фактора A. Двухфакторный анализ с группировкой с описывается моделью:


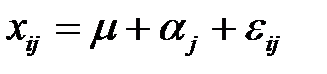 При использовании стандартных методов дисперсионного анализа должно удовлетворяться условие равенства дисперсий остаточных случайных величин. Если нет уверенности в том, что данное условие выполняется, следует проводить проверку однородности дисперсий. Например, в модели однофакторного дисперсионного анализа
При использовании стандартных методов дисперсионного анализа должно удовлетворяться условие равенства дисперсий остаточных случайных величин. Если нет уверенности в том, что данное условие выполняется, следует проводить проверку однородности дисперсий. Например, в модели однофакторного дисперсионного анализа Пусть из k совокупностей взяты выборки объемами n 1, n 2,... n k и получены оценки дисперсии:
Пусть из k совокупностей взяты выборки объемами n 1, n 2,... n k и получены оценки дисперсии: Тогда для объединенной оценки дисперсии при справедливости нулевой гипотезы H0: σ 12 = σ 22 = … = σk 2 получим:
Тогда для объединенной оценки дисперсии при справедливости нулевой гипотезы H0: σ 12 = σ 22 = … = σk 2 получим: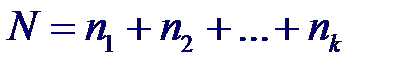

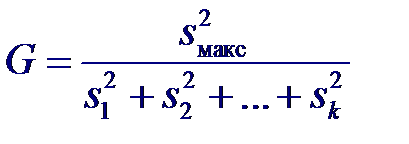

 Вычислим при каждом значении фактора Aj, т. е. для j -го столбца таблицы рангов, значения средних рангов R.j
Вычислим при каждом значении фактора Aj, т. е. для j -го столбца таблицы рангов, значения средних рангов R.j



 Другая форма записи этой статистики, удобная для вычислений, имеет вид
Другая форма записи этой статистики, удобная для вычислений, имеет вид
 Если в таблице данных есть совпадающие значения, необходимо при их ранжировании и переходе к таблице рангов использовать средние ранги. Если совпадений много, то рекомендуется применять модифицированную форму статистики H:
Если в таблице данных есть совпадающие значения, необходимо при их ранжировании и переходе к таблице рангов использовать средние ранги. Если совпадений много, то рекомендуется применять модифицированную форму статистики H:


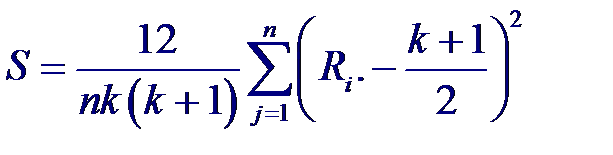 Отсюда статистика Фридмана, используемая для проверки нулевой гипотезы, будет определяться как
Отсюда статистика Фридмана, используемая для проверки нулевой гипотезы, будет определяться как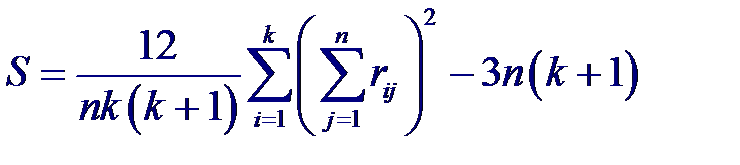
 При функциональных преобразованиях случайных величин вида Y = ϕ (X) для нахождения математического ожидания и дисперсии случайной величины Y достаточно знать закон распределения случайной величины X:
При функциональных преобразованиях случайных величин вида Y = ϕ (X) для нахождения математического ожидания и дисперсии случайной величины Y достаточно знать закон распределения случайной величины X:
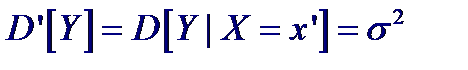

 Первое слагаемое обусловливает вклад в дисперсию от функциональной зависимости Y = ϕ (X), а второе – случайный разброс вокруг математического ожидания M [ ϕ (X)]. Введем понятие квадрата корреляционного отношения
Первое слагаемое обусловливает вклад в дисперсию от функциональной зависимости Y = ϕ (X), а второе – случайный разброс вокруг математического ожидания M [ ϕ (X)]. Введем понятие квадрата корреляционного отношения




 Коэффициент корреляции являются измерителям степени тесноты линейной статистической связи между случайными величинами. Формально его можно вычислить для любой двумерной системы случайных величин, однако только для совместной нормальной совокупности коэффициент корреляции имеет четкий смысл как характеристика тесноты связи.
Коэффициент корреляции являются измерителям степени тесноты линейной статистической связи между случайными величинами. Формально его можно вычислить для любой двумерной системы случайных величин, однако только для совместной нормальной совокупности коэффициент корреляции имеет четкий смысл как характеристика тесноты связи.


