
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистических гипотезСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистической гипотезой называется всякое предположение о генеральной совокупности, проверяемое по выборке. Статистические гипотезы делятся на: параметрические – сформулированные относительно параметров (среднего значения, доли, дисперсии и др.) распределения известного вида; непараметрические – сформулированные относительно вида распределения (например, оценка по выборке нормальности генеральной совокупности). Выдвигаемая гипотеза называется основной или нулевой (Н0). Гипотеза, противоположная нулевой, называется конкурирующей или альтернативной (Н1). Так как проверка статистических гипотез осуществляется по выборочным данным, то возникает возможность принятия ошибочных решений. Различают ошибки первого и второго рода. Ошибка первого рода заключается в том, что будет отвергнута правильная гипотеза, т.е. когда в действительности верна Н0 гипотеза, а в результате проверки она была отвергнута и принята гипотеза Н1. Вероятность ошибки первого рода называется уровнем значимости и обозначается
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, т.е. в действительности верна некоторая альтернативная гипотеза, а по выборочным данным была принята неверная гипотеза Н0. Вероятность ошибка второго рода обозначается
Существует правильное решение двух видов:
Статистическим критерием (К) называют случайную величину, с помощью которой при Проверка статистических гипотез обычно осуществляется в определенной последовательности. 1. Располагая выборочными данными, формулируют нулевую и конкурирующую гипотезы. 2. Задают уровень значимости 3. Выбирают критерий К, по которому будет проверяться выдвинутая гипотеза. Обычно используют следующие распределения критериев: u – нормальное распределение: t – распределение Стьюдента; F – распределение Фишера - Снедекора. 4. На основании выборочных данных определяют фактически наблюдаемое значение критерия Кн. 5. В зависимости от вида альтернативной гипотезы находят, по соответствующей таблице, критические значения критерия для двусторонней
1 Имеется распределение сельскохозяйственных предприятий Краснодарского края по урожайности озимой пшеницы. Требуется проверить нулевую гипотезу, что совокупность предприятий по урожайности озимой пшеницы распределяется по нормальному закону. Уровень значимости принять равным 0,05. Таблица 10 – Распределение предприятий по урожайности озимой пшеницы
2 Выборочным методом изучались цены на картофель на продовольственных рынках города. Получено следующее распределение продавцов по уровню цен. Таблица 11 – Распределение продавцов по цене на картофель
При уровне значимости 0,05 проверить нулевую гипотезу, что цена на картофель на продовольственных рынках города распределяется по нормальному закону. 3 Сельскохозяйственные предприятия области по урожайности озимой пшеницы распределяются по нормальному закону с известным средним квадратическим отклонением При уровне значимости а) б) в) 4 Производитель печенья утверждает, что вес одной пачки составляет 200 г. Выборочное взвешивание 10 пачек дало следующие результаты: 198; 197; 199; 200; 197; 201; 199; 195; 197; 200. При уровне значимости 5 Сливочное масло фасуется в пачки средним весом 170 г и средним квадратическим отклонением 3 г. Случайная выборка 20 пачек масла показала, что средний вес одной пачки равен 170,3 г. Проверить статистическую гипотезу при уровне значимости 0,05 о соответствии веса случайно взятой пачки масла, установленному весу.
6 Две фирмы производят однотипный товар. Утверждается, что 90% товаров первой фирмы реализуется повышенного качества, а второй фирмы 80 %. При выборочной проверке оказалось, что из 80 единиц товара первой фирмы повышенного качества 75, а из 60 единиц товара второй фирмы оказалось 45 единиц повышенного качества. При уровне значимости 7 Провести две случайные выборки по одному из показателей приложения 4, объемами n1 и n2. Проверить нулевую гипотезу о равенстве выборочных средних значений, при уровне значимости 0,05 (предполагается, что дисперсии неизвестны и одинаковы): а) n1 = n2 =20; б) n1 = 20; n2 =15. 8 Проводилось испытание 8 сортов озимой пшеницы. Каждый сорт высевался на 6 делянках одинаковой площади. При 5% уровне значимости проверить гипотезу о существенности различий в средней урожайности двух сортов озимой пшеницы (номера сортов даются студенту преподавателем). Таблица 12 - Урожайность озимой пшеницы, ц/га
9 Произведено выборочное обследование 10% приусадебных участков восьми районов случайным бесповторным способом. Получены следующие результаты об урожайности овощей.
Таблица 13 – Урожайность овощей в хозяйствах населения
При уровне значимости 0,05 по двум районам проверить гипотезы о равенстве: дисперсий, средних выборочных урожайностей, долей посевов овощей в площади приусадебных участков.
10 При уровне значимости 0,05 проверить гипотезу о равенстве успеваемости студентов по теории вероятностей и математике.
Таблица 14 – Оценки студентов на экзаменах
11 - Результаты выступлений 10 спортсменов оценивались двумя судьями по десятибалльной шкале.
Таблица 15 – Оценки судей результатов соревнований спортсменов
При уровне значимости 0,05 проверить гипотезу о значимости различий в оценке выступлений спортсменов двумя судьями.
12 Определенные сорта озимой пшеницы испытывались на одинаковом числе участков, на протяжении семи лет. При уровне значимости
Таблица 16 – Урожайность озимой пшеницы по участкам
13 Имеются данные о числе сорняков в пробах семян помидор
Таблица 17 – Число сорняков в пробах
Проверить гипотезу о соответствии данного эмпирического вариационного ряда распределению Пуассона. Уровень значимости принять равным 0,05. ДИСПЕРСИОННЫЙ АНАЛИЗ Сущность дисперсионного анализа заключается в том, что дисперсия изучаемого признака разлагается на сумму составляющих ее дисперсий, каждое слагаемое которой соответствует действию определенного источника изменчивости. Например, в однофакторном анализе мы получим разложение вида:
где
В дисперсионном анализе рассматривается нулевая гипотеза – ни один из рассматриваемых факторов не оказывает влияние на изменчивость признака. Расчеты проводятся в следующей последовательности: - определяются необходимые суммы квадратов отклонений результативного признака, в соответствии с моделью дисперсионного анализа; - находится число степеней свободы вариации по каждому источнику; - рассчитываются средние квадраты отклонений; - определяются наблюдаемые и критические значения критерия F – Фишера – Снедекора, формулируются выводы относительно гипотезы Н0; - оценивается значимость различий групповых средних по вариантам опыта. Если Fн Рассмотрим алгоритм однофакторного дисперсионного анализа. Определенный фактор принимает p различных уровней и на каждой уровне сделано n наблюдений, что дает N=np наблюдений. Данные обычно располагают в виде таблицы результатов Xij (i=1,2,…,p; j=1,2,….,n):
Рассматриваем тождество
(Точка вместо индекса обозначает усреднение соответствующих наблюдений по этому индексу.) Иначе можно записать: SSo=SSv+SSz. Величина факторной суммы квадратов отклонений SSv вычисляется по отклонениям p средних от общей средней
Таблица 18 - Однофакторный дисперсионный анализ
Если гипотеза о том, что влияние всех уровней одинаково, справедлива, то обе величины Если Fн Для оценки существенности частых различий вычисляют: а) среднюю ошибку средней арифметической
б) ошибку разности средних
в) наименьшую существенную разность
Сравнивая разности средних значений
1 Оценить существенность различий в успеваемости студентов по четырем предметам и группам. Численность студентов в каждой группе составляет 25 человек.
Таблица 19 - Уровень успеваемости студентов, балл
2 Доказывает ли опыт влияние различных доз удобрений на урожайность озимой пшеницы
Таблица 20 - Урожайность озимой пшеницы с 1 га, ц
3 Оценить различия в среднемесячной заработной плате механизаторов различной квалификации.
Таблица 21 – Средняя месячная заработная плата механизаторов, тыс. руб.
4 Оценить существенность влияния различных сортов и доз удобрений на урожайность риса.
Таблица 22 - Урожайность риса с 1га, ц
5 Оценить существенность различий уровня производительности механизаторов при культивации в различных хозяйствах по пропашным культурам и стажу работы механизаторов. Таблица 23 - Объем выполненных работ механизаторами за 1 час работы, эт. га
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.163.23 (0.014 с.) |

 .
. . (13.1)
. (13.1) .
. . (13.2)
. (13.2) и
и  . (13.3)
. (13.3) имают решение о принятии или отклонений нулевой гипотезы.
имают решение о принятии или отклонений нулевой гипотезы.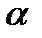 (обычно принимают
(обычно принимают  =0,1; 0,01;
=0,1; 0,01; 
 распределение Пирсона (xu – квадрат);
распределение Пирсона (xu – квадрат); или односторонней области (
или односторонней области ( или
или  ). Если фактически наблюдаемые значения критерия попадают в критическую область, то нулевая гипотеза отвергается. В противном случае принимается нулевая гипотеза и считается, что она не противоречит выборочным данным (при этом существует возможность ошибки с вероятностью равной
). Если фактически наблюдаемые значения критерия попадают в критическую область, то нулевая гипотеза отвергается. В противном случае принимается нулевая гипотеза и считается, что она не противоречит выборочным данным (при этом существует возможность ошибки с вероятностью равной  ц/га и генеральной средней урожайностью
ц/га и генеральной средней урожайностью 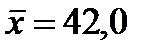 ц/га. Из генеральной совокупности извлечена выборка 50 хозяйств, по которой определена выборочная средняя урожайность
ц/га. Из генеральной совокупности извлечена выборка 50 хозяйств, по которой определена выборочная средняя урожайность  ц/га.
ц/га. проверить нулевую гипотезу, что:
проверить нулевую гипотезу, что:


 проверить гипотезы: а) о соответствии выборочных долей продукции высшего качества заявленной доле; б) о значимости различий в доле продукции высшего качества двух фирм.
проверить гипотезы: а) о соответствии выборочных долей продукции высшего качества заявленной доле; б) о значимости различий в доле продукции высшего качества двух фирм. а в двухфакторном:
а в двухфакторном: 
 -общая дисперсия изучаемого признака С;
-общая дисперсия изучаемого признака С;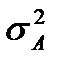 - дисперсия, вызванная влиянием фактора А;
- дисперсия, вызванная влиянием фактора А;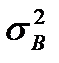 - дисперсия, вызванная влиянием фактора В;
- дисперсия, вызванная влиянием фактора В; - дисперсия, вызванная взаимодействием факторов А и В;
- дисперсия, вызванная взаимодействием факторов А и В; - дисперсия, вызванная неучтенными случайными причинами (случайная дисперсия);
- дисперсия, вызванная неучтенными случайными причинами (случайная дисперсия);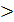 Fкр, то делается вывод о сущности различий результативного признака, обусловленных влиянием признака – фактора, т.е. действие фактора на результативный признак признается статистически достоверным.
Fкр, то делается вывод о сущности различий результативного признака, обусловленных влиянием признака – фактора, т.е. действие фактора на результативный признак признается статистически достоверным.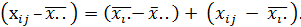 Суммируя обе части уравнения по i и j
Суммируя обе части уравнения по i и j  и проведя преобразования, получим:
и проведя преобразования, получим:
 .., поэтому Sv имеет (p-1) степеней свободы. Величина остаточной суммы квадратов отклонений SSz вычисляется по отклонениям N наблюдений от p выборочных средних и, следовательно, имеет N-p=np-p=p (n-1) степеней свободы. Общая сумма квадратов отклонений SSo имеет (N-1) степеней свободы.
.., поэтому Sv имеет (p-1) степеней свободы. Величина остаточной суммы квадратов отклонений SSz вычисляется по отклонениям N наблюдений от p выборочных средних и, следовательно, имеет N-p=np-p=p (n-1) степеней свободы. Общая сумма квадратов отклонений SSo имеет (N-1) степеней свободы.




 и
и  будет несмещенными оценками
будет несмещенными оценками  . Значит, гипотезу можно проверить, вычислив отношение
. Значит, гипотезу можно проверить, вычислив отношение  Fкр, то гипотеза о незначимом влиянии фактора A на результат наблюдений не принимается. В этом случае оценивается значимость различий между средними результативного признака по уровням факторного признака.
Fкр, то гипотеза о незначимом влиянии фактора A на результат наблюдений не принимается. В этом случае оценивается значимость различий между средними результативного признака по уровням факторного признака.

 .
. по вариантам с HCP, делают вывод о существенности различий в уровне средних.
по вариантам с HCP, делают вывод о существенности различий в уровне средних.


