
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое оценивание. Статистическая гипотеза.Содержание книги
Поиск на нашем сайте
Статистическое оценивание. Статистическая гипотеза. 1. Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок 2. Статистическая гипотеза. 3. Критерии для проверки гипотезы 4. Критерий Пирсона для проверки гипотезы о виде закона распределения случайной величины. 5. Критерий Колмогорова Статистическая гипотеза. Определение 11.1. Статистической гипотезой называют гипотезу о виде неизвестного распределения генеральной совокупности или о параметрах известных распределений. Определение 11.2. Нулевой (основной) называют выдвинутую гипотезу Н0. Конкурирую-щей (альтернативной) называют гипотезу Н1, которая противоречит нулевой. Пример. Пусть Н0 заключается в том, что математическое ожидание генеральной совокупности а = 3. Тогда возможные варианты Н1: а) а ≠ 3; б) а > 3; в) а < 3. Определение 11.3. Простой называют гипотезу, содержащую только одно предположение, сложной – гипотезу, состоящую из конечного или бесконечного числа простых гипотез. Пример. Для показательного распределения гипотеза Н0: λ = 2 – простая, Н0: λ > 2 – сложная, состоящая из бесконечного числа простых (вида λ = с, где с – любое число, большее 2). В результате проверки правильности выдвинутой нулевой гипотезы (такая проверка называется статистической, так как производится с применением методов математической статистики) возможны ошибки двух видов: 1. ошибка первого рода, состоящая в том, что будет отвергнута правильная нулевая гипотеза; 2. ошибка второго рода, заключающаяся в том, что будет принята неверная гипотеза. Замечание. Какая из ошибок является на практике более опасной, зависит от конкретной задачи. Например, если проверяется правильность выбора метода лечения больного, то ошибка первого рода означает отказ от правильной методики, что может замедлить лечение, а ошибка второго рода (применение неправильной методики) чревата ухудшением состояния больного и является более опасной. Определение 11.4. Вероятность ошибки первого рода называется уровнем значимости α. Основной прием проверки статистических гипотез заключается в том, что по имеющейся выборке вычисляется значение некоторой случайной величины, имеющей известный закон распределения. Определение 11.5. Статистическим критерием называется случайная величина К с известным законом распределения, служащая для проверки нулевой гипотезы. Определение 11.6. Критической областью называют область значений критерия, при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают.
Процесс проверки гипотезы состоит из следующих этапов: 1. выбирается статистический критерий К; 2. вычисляется его наблюдаемое значение Кнабл по имеющейся выборке; 3. поскольку закон распределения К известен, определяется (по известному уровню значимости α) критическое значение kкр, разделяющее критическую область и область принятия гипотезы (например, если р(К > kкр) = α, то справа от kкр располагается критическая область, а слева – область принятия гипотезы); 4. если вычисленное значение Кнабл попадает в область принятия гипотезы, то нулевая гипотеза принимается, если в критическую область – нулевая гипотеза отвергается. Различают разные виды критических областей: - правостороннюю критическую область, определяемую неравенством K > kкр (kкр > 0); - левостороннюю критическую область, определяемую неравенством K < kкр (kкр < 0); - двустороннюю критическую область, определяемую неравенствами K < k1, K > k2 (k2 > k1). Определение 11.7. Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что верна конкурирующая гипотеза. Если обозначить вероятность ошибки второго рода (принятия неправильной нулевой гипотезы) β, то мощность критерия равна 1 – β. Следовательно, чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода. Поэтому после выбора уровня значимости следует строить критическую область так, чтобы мощность критерия была максимальной. Критерий Колмогорова. Этот критерий применяется для проверки простой гипотезы Н0 о том, что независимые одинаково распределенные случайные величины Х1, Х2, …, Хп имеют заданную непрерывную функцию распределения F(x). Найдем функцию эмпирического распределения Fn(x) и будем искать границы двусторонней критической области, определяемой условием
А.Н.Колмогоров доказал, что в случае справедливости гипотезы Н0 распределение статистики Dn не зависит от функции F(x), и при
где - критерий Колмогорова, значения которого можно найти в соответствующих таблицах. Критическое значение критерия λп(α) вычисляется по заданному уровню значимости α как корень уравнения Можно показать, что приближенное значение вычисляется по формуле
где z – корень уравнения На практике для вычисления значения статистики Dn используется то, что
а Можно дать следующее геометрическое истолкование критерия Колмогорова: если изобразить на плоскости Оху графики функций Fn(x), Fn(x) ±λn(α) (рис. 1), то гипотеза Н0 верна, если график функции F(x) не выходит за пределы области, лежащей между графиками функций Fn(x) -λn(α) и Fn(x) +λn(α).
Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов асимметрии и эксцесса.
Определим по аналогии с соответствующими понятиями для теоретического распределения асимметрию и эксцесс эмпирического распределения.
Определение 11.8. Асимметрия эмпирического распределения определяется равенством
где т3 – центральный эмпирический момент третьего порядка. Эксцесс эмпирического распределения определяется равенством
где т4 – центральный эмпирический момент четвертого порядка. Как известно, для нормально распределенной случайной величины асимметрия и эксцесс равны 0. Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что генеральная совокупность распределена по нормальному закону.
Лекция 12. Ранговая корреляция. Пусть объекты генеральной совокупности обладают двумя качественными признаками (то есть признаками, которые невозможно измерить точно, но которые позволяют сравнивать объекты между собой и располагать их в порядке убывания или возрастания качества). Договоримся для определенности располагать объекты в порядке ухудшения качества. Пусть выборка объема п содержит независимые объекты, обладающие двумя качествен-ными признаками: А и В. Требуется выяснить степень их связи между собой, то есть установить наличие или отсутствие ранговой корреляции. Расположим объекты выборки в порядке ухудшения качества по признаку А, предполагая, что все они имеют различное качество по обоим признакам. Назовем место, занимаемое в этом ряду некоторым объектом, его рангом хi: х1 = 1, х2 = 2,…, хп = п. Теперь расположим объекты в порядке ухудшения качества по признаку В, присвоив им ранги уi, где номер i равен порядковому номеру объекта по признаку А, а само значение ранга равно порядковому номеру объекта по признаку В. Таким образом, получены две последовательности рангов: по признаку А … х1, х2,…, хп по признаку В … у1, у2,…, уп. При этом, если, например, у3 = 6, то это означает, что данный объект занимает в ряду по признаку А третье место, а в ряду по признаку В – шестое. Сравним полученные последовательности рангов. Если xi = yi при всех значениях i, то ухудшение качества по признаку А влечет за собой ухудшение качества по признаку В, то есть имеется «полная ранговая зависимость». Если ранги противоположны, то есть х1 = 1, у1 = п; х2 = 2, у2 = п – 1;…, хп = п, уп = 1, то признаки тоже связаны: ухудшение качества по одному из них приводит к улучшению качества по другому («противоположная зависимость»). На практике чаще всего встречается промежуточный случай, когда ряд уi не монотонен. Для оценки связи между признаками будем считать ранги х1, х2,…, хп возможными значениями случайной величины Х, а у1, у2,…, уп – возможными значениями случайной величины Y. Теперь можно исследовать связь между Х и Y, вычислив для них выборочный коэффициент корреляции
где
Итак, требуется найти Можно показать, что
Регрессионный анализ. Рассмотрим выборку двумерной случайной величины (Х, Y). Примем в качестве оценок условных математических ожиданий компонент их условные средние значения, а именно: условным средним M (Y / x) = f (x), M (X / y) = φ (y). Условные средние
- выборочное уравнение регрессии Y на Х,
- выборочное уравнение регрессии Х на Y. Соответственно функции f*(x) и φ*(у) называются выборочной регрессией Y на Х и Х на Y, а их графики – выборочными линиями регрессии. Выясним, как определять параметры выборочных уравнений регрессии, если сам вид этих уравнений известен. Пусть изучается двумерная случайная величина (Х, Y), и получена выборка из п пар чисел (х1, у1), (х2, у2),…, (хп, уп). Будем искать параметры прямой линии среднеквадратической регрессии Y на Х вида Y = ρyxx + b, (12.10) Подбирая параметры ρух и b так, чтобы точки на плоскости с координатами (х1, у1), (х2, у2), …, (хп, уп) лежали как можно ближе к прямой (12.10). Используем для этого метод наименьших квадратов и найдем минимум функции
Приравняем нулю соответствующие частные производные:
В результате получим систему двух линейных уравнений относительно ρ и b:
Ее решение позволяет найти искомые параметры в виде:
При этом предполагалось, что все значения Х и Y наблюдались по одному разу. Теперь рассмотрим случай, когда имеется достаточно большая выборка (не менее 50 значений), и данные сгруппированы в виде корреляционной таблицы
Здесь nij – число появлений в выборке пары чисел (xi, yj). Поскольку
Можно решить эту систему и найти параметры ρух и b, определяющие выборочное уравнение прямой линии регрессии:
Но чаще уравнение регрессии записывают в ином виде, вводя выборочный коэффициент корреляции. Выразим b из второго уравнения системы (12.14):
Подставим это выражение в уравнение регрессии:
где
и умножим равенство (22.8) на
Статистическое оценивание. Статистическая гипотеза. 1. Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок 2. Статистическая гипотеза. 3. Критерии для проверки гипотезы 4. Критерий Пирсона для проверки гипотезы о виде закона распределения случайной величины. 5. Критерий Колмогорова
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.14.104 (0.008 с.) |

 . (11.10)
. (11.10)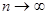
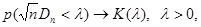
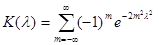 - (11.12)
- (11.12)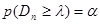 .
.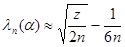 ,
,
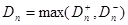 , где
, где 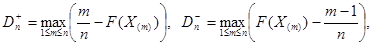
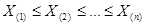 - вариационный ряд, построенный по выборке Х1, Х2, …, Хп.
- вариационный ряд, построенный по выборке Х1, Х2, …, Хп. х
х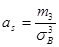 , (11.13)
, (11.13)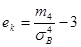 , (11.14)
, (11.14)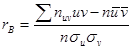 , (12.2)
, (12.2)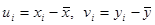 (условные варианты). Поскольку каждому рангу xi соответствует только одно значение yi, то частота любой пары условных вариант с одинаковыми индексами равна 1, а с разными индексами – нулю. Кроме того, из выбора условных вариант следует, что
(условные варианты). Поскольку каждому рангу xi соответствует только одно значение yi, то частота любой пары условных вариант с одинаковыми индексами равна 1, а с разными индексами – нулю. Кроме того, из выбора условных вариант следует, что  , поэтому формула (21.2) приобретает более простой вид:
, поэтому формула (21.2) приобретает более простой вид: . (12.3)
. (12.3)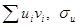 и
и  .
. . Учитывая, что
. Учитывая, что 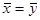 , можно выразить
, можно выразить 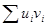 через разности рангов
через разности рангов 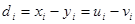 . После преобразований получим:
. После преобразований получим:  ,
, 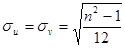 , откуда
, откуда 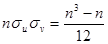 . Подставив эти результаты в (21.3), получим выборочный коэффициент ранговой корреляции Спирмена:
. Подставив эти результаты в (21.3), получим выборочный коэффициент ранговой корреляции Спирмена: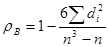 . (12.4)
. (12.4) назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее
назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее 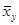 - среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. В лекции 11 были выведены уравнения регрессии Y на Х и Х на Y:
- среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. В лекции 11 были выведены уравнения регрессии Y на Х и Х на Y: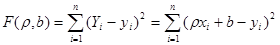 . (12.11)
. (12.11)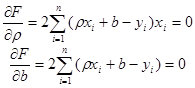 .
.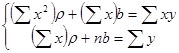 . (12.12)
. (12.12)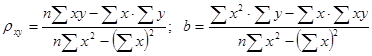 . (12.13)
. (12.13)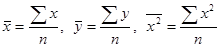 , заменим в системе (22.5)
, заменим в системе (22.5) 
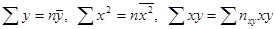 , где пху – число появлений пары чисел (х, у). Тогда система (22.5) примет вид:
, где пху – число появлений пары чисел (х, у). Тогда система (22.5) примет вид: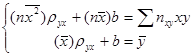 . (12.14)
. (12.14)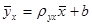 .
.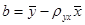 .
.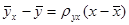 . Из (12.14)
. Из (12.14) , (12.15)
, (12.15) Введем понятие выборочного коэффициента корреляции
Введем понятие выборочного коэффициента корреляции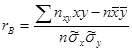
 :
: 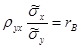 , откуда
, откуда 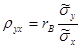 . Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида
. Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида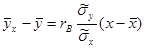 . (12.16)
. (12.16)


