
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия генеральной совокупности неизвестна.Содержание книги
Поиск на нашем сайте
В этом случае выберем в качестве критерия случайную величину
где S – исправленное среднее квадратическое отклонение. Такая случайная величина имеет распределение Стьюдента с k = n – 1 степенями свободы. Рассмотрим те же, что и в предыдущем случае, конкурирующие гипотезы и соответствующие им критические области. Предварительно вычислим наблюдаемое значение критерия:
- если Н1: М( Если | Tнабл | < tдвуст.кр., то нулевая гипотеза принимается. Если | Tнабл | > tдвуст.кр., то нулевая гипотеза отвергается. - если Н1: М( Tнабл < tправост.кр.. - при конкурирующей гипотезе Н1: М(
3. Критерий для проверки гипотезы о сравнении двух дисперсий.
Пусть имеются две нормально распределенные генеральные совокупности Х и Y. Из них извлечены независимые выборки объемов соответственно п1 и п2, по которым вычислены исправленные выборочные дисперсии Н0: М ( Замечание. Конечно, исправленные дисперсии, вычисленные по выборкам, обычно оказываются различными. При проверке гипотезы выясняется, является ли это различие незначимым и обусловленным случайными причинами (в случае принятия нулевой гипотезы) или оно является следствием того, что сами генеральные дисперсии различны. В качестве критерия примем случайную величину
- отношение большей выборочной дисперсии к меньшей. Она имеет распределение Фишера-Снедекора со степенями свободы k1 = n1 – 1 и k2 = n2 – 1, где п1 – объем выборки, по которой вычислена большая исправленная дисперсия, а п2 – объем второй выборки.
Рассмотрим два вида конкурирующих гипотез: ü пусть Н1: D(X) > D(Y). Наблюдаемым значением критерия будет отношение большей из исправленных дисперсий к меньшей: ü если Н1: D(X) ≠ D(Y), то критическая область является двусторонней и определяется неравенствами F < F1, F > F2, где р(F < F1) = р(F > F2) = α/2. При этом достаточно найти правую критическую точку F2 = Fкр (
4. Критерий Пирсона для проверки гипотезы о виде закона распределения случайной величины . Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения. 1. Проверка гипотезы о нормальном распределении. Пусть получена выборка достаточно большого объема п с большим количеством различных значений вариант. Доя удобства ее обработки разделим интервал от наименьшего до наибольшего из значений вариант на s равных частей и будем считать, что значения вари ант, попавших в каждый интервал, приближенно равны числу, задающему середину интервала. Подсчитав число вариант, попавших в каждый интервал, составим так называемую сгруппированную выборку: варианты………..х1 х2 … хs частоты………….п1 п2 … пs, где хi – значения середин интервалов, а пi – число вариант, попавших в i-й интервал (эмпи-рические частоты). По полученным данным можно вычислить выборочное среднее
где аi и bi - границы i-го интервала. Умножив полученные вероятности на объем выборки п, найдем теоретические частоты: пi =n·pi. Наша цель – сравнить эмпирические и теоретические частоты, которые, конечно, отличаются друг от друга, и выяснить, являются ли эти различия несущественными, не опровергающими гипотезу о нормальном распределении исследуемой случайной величины, или они настолько велики, что противоречат этой гипотезе. Для этого используется критерий в виде случайной величины
Смысл ее очевиден: суммируются части, которые квадраты отклонений эмпирических частот от теоретических составляют от соответствующих теоретических частот. Можно доказать, что вне зависимости от реального закона распределения генеральной совокупно-сти закон распределения случайной величины (11.8) при
где α – уровень значимости. Следовательно, критическая область задается неравенством Итак, для проверки нулевой гипотезы Н0: генеральная совокупность распределена нормально – нужно вычислить по выборке наблюдаемое значение критерия:
а по таблице критических точек распределения χ2 найти критическую точку
2. Проверка гипотезы о равномерном распределении. При использовании критерия Пирсона для проверки гипотезы о равномерном распределении генеральной совокупности с предполагаемой плотностью вероятности
необходимо, вычислив по имеющейся выборке значение
где а* и b* - оценки а и b. Действительно, для равномерного распределения М(Х) = Затем, предполагая, что
Здесь s – число интервалов, на которые разбита выборка. Наблюдаемое значение критерия Пирсона вычисляется по формуле (11.8), а критическое – по таблице с учетом того, что число степеней свободы k = s – 3. После этого границы критической области определяются так же, как и для проверки гипотезы о нормальном распределении. 3. Проверка гипотезы о показательном распределении. В этом случае, разбив имеющуюся выборку на равные по длине интервалы, рассмотрим последовательность вариант
Затем сравниваются наблюдаемое и критическое значение критерия Пирсона с учетом того, что число степеней свободы k = s – 2.
Критерий Колмогорова. Этот критерий применяется для проверки простой гипотезы Н0 о том, что независимые одинаково распределенные случайные величины Х1, Х2, …, Хп имеют заданную непрерывную функцию распределения F(x). Найдем функцию эмпирического распределения Fn(x) и будем искать границы двусторонней критической области, определяемой условием
А.Н.Колмогоров доказал, что в случае справедливости гипотезы Н0 распределение статистики Dn не зависит от функции F(x), и при
где - критерий Колмогорова, значения которого можно найти в соответствующих таблицах. Критическое значение критерия λп(α) вычисляется по заданному уровню значимости α как корень уравнения Можно показать, что приближенное значение вычисляется по формуле
где z – корень уравнения На практике для вычисления значения статистики Dn используется то, что
а Можно дать следующее геометрическое истолкование критерия Колмогорова: если изобразить на плоскости Оху графики функций Fn(x), Fn(x) ±λn(α) (рис. 1), то гипотеза Н0 верна, если график функции F(x) не выходит за пределы области, лежащей между графиками функций Fn(x) -λn(α) и Fn(x) +λn(α).
Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов асимметрии и эксцесса.
Определим по аналогии с соответствующими понятиями для теоретического распределения асимметрию и эксцесс эмпирического распределения.
Определение 11.8. Асимметрия эмпирического распределения определяется равенством
где т3 – центральный эмпирический момент третьего порядка. Эксцесс эмпирического распределения определяется равенством
где т4 – центральный эмпирический момент четвертого порядка. Как известно, для нормально распределенной случайной величины асимметрия и эксцесс равны 0. Поэтому, если соответствующие эмпирические величины достаточно малы, можно предположить, что генеральная совокупность распределена по нормальному закону.
Лекция 12.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.69.109 (0.011 с.) |

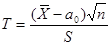 , (11.4)
, (11.4)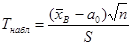 . (11.5)
. (11.5) ) ≠ а0, то критическая точка tдвуст.кр. находится по таблице критических точек распределения Стьюдента по известным α и k = n – 1.
) ≠ а0, то критическая точка tдвуст.кр. находится по таблице критических точек распределения Стьюдента по известным α и k = n – 1.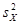 и
и 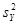 . Требуется при заданном уровне значимости α проверить нулевую гипотезу Н0: D(X) = D(Y) о равенстве дисперсий рассматриваемых генеральных совокупностей. Учитывая несмещенность исправленных выборочных дисперсий, можно записать нулевую гипотезу так:
. Требуется при заданном уровне значимости α проверить нулевую гипотезу Н0: D(X) = D(Y) о равенстве дисперсий рассматриваемых генеральных совокупностей. Учитывая несмещенность исправленных выборочных дисперсий, можно записать нулевую гипотезу так: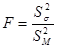 - (11.7)
- (11.7)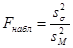 . По таблице критических точек распределения Фишера-Снедекора можно найти критическую точку Fнабл(α; k1; k2). При Fнабл < Fкр нулевая гипотеза принимается, при Fнабл > Fкр отвергается.
. По таблице критических точек распределения Фишера-Снедекора можно найти критическую точку Fнабл(α; k1; k2). При Fнабл < Fкр нулевая гипотеза принимается, при Fнабл > Fкр отвергается. , k1, k2). Тогда при Fнабл < Fкр нулевая гипотеза принимается, при Fнабл > Fкр отвергается.
, k1, k2). Тогда при Fнабл < Fкр нулевая гипотеза принимается, при Fнабл > Fкр отвергается. и выборочное среднее квадратическое отклонение σВ. Проверим предположение, что генеральная совокупность распределена по нормальному закону с параметрами M(X) =
и выборочное среднее квадратическое отклонение σВ. Проверим предположение, что генеральная совокупность распределена по нормальному закону с параметрами M(X) = 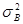 . Тогда можно найти количество чисел из выборки объема п, которое должно оказаться в каждом интервале при этом предположении (то есть теоретические частоты). Для этого по таблице значений функции Лапласа найдем вероятность попадания в i-й интервал:
. Тогда можно найти количество чисел из выборки объема п, которое должно оказаться в каждом интервале при этом предположении (то есть теоретические частоты). Для этого по таблице значений функции Лапласа найдем вероятность попадания в i-й интервал: ,
,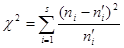 . (11.8)
. (11.8)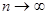 стремится к закону распределения
стремится к закону распределения  с числом степеней свободы k = s – 1 – r, где r – число параметров предполагаемого распределения, оцененных по данным выборки. Нормальное распределение характеризуется двумя параметрами, поэтому k = s – 3. Для выбранного критерия строится правосторонняя критическая область, определяемая условием
с числом степеней свободы k = s – 1 – r, где r – число параметров предполагаемого распределения, оцененных по данным выборки. Нормальное распределение характеризуется двумя параметрами, поэтому k = s – 3. Для выбранного критерия строится правосторонняя критическая область, определяемая условием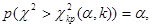 (11.9)
(11.9) а область принятия гипотезы -
а область принятия гипотезы - 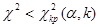 .
.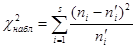 , (11.10)
, (11.10)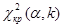 , используя известные значения α и k = s – 3. Если
, используя известные значения α и k = s – 3. Если 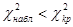 - нулевую гипотезу принимают, при
- нулевую гипотезу принимают, при  ее отвергают.
ее отвергают.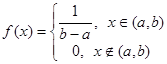
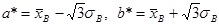 , (11.11)
, (11.11)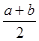 ,
, 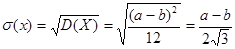 , откуда можно получить систему для определения а* и b*:
, откуда можно получить систему для определения а* и b*:  , решением которой являются выражения (11.10).
, решением которой являются выражения (11.10).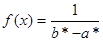 , можно найти теоретические частоты по формулам
, можно найти теоретические частоты по формулам
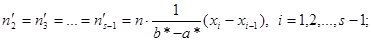
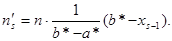
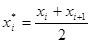 , равноотстоящих друг от друга (считаем, что все варианты, попавшие в i – й интервал, принимают значение, совпадающее с его серединой), и соответствующих им частот ni (число вариант выборки, попавших в i – й интервал). Вычислим по этим данным
, равноотстоящих друг от друга (считаем, что все варианты, попавшие в i – й интервал, принимают значение, совпадающее с его серединой), и соответствующих им частот ni (число вариант выборки, попавших в i – й интервал). Вычислим по этим данным 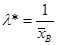 . Тогда теоретические частоты вычисляются по формуле
. Тогда теоретические частоты вычисляются по формуле
 . (11.10)
. (11.10)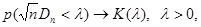
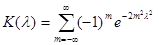 - (11.12)
- (11.12)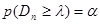 .
.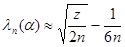 ,
,
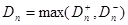 , где
, где 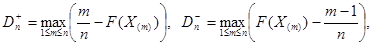
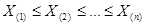 - вариационный ряд, построенный по выборке Х1, Х2, …, Хп.
- вариационный ряд, построенный по выборке Х1, Х2, …, Хп. х
х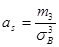 , (11.13)
, (11.13)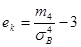 , (11.14)
, (11.14)


