
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный анализ и регрессионный анализСодержание книги
Поиск на нашем сайте
1. Проверка гипотезы о значимости выборочного коэффициента корреляции. 2. Ранговая корреляция. 3. Свойства выборочного коэффициента корреляции Спирмена. 4. Регрессионный анализ. 5. Однофакторный дисперсионный анализ. Проверка гипотезы о значимости выборочного коэффициента корреляции. Рассмотрим выборку объема п, извлеченную из нормально распределенной двумерной генеральной совокупности (X, Y). Вычислим выборочный коэффициент корреляции rB. Пусть он оказался не равным нулю. Это еще не означает, что и коэффициент корреляции генеральной совокупности не равен нулю. Поэтому при заданном уровне значимости α возникает необходимость проверки нулевой гипотезы Н0: rг = 0 о равенстве нулю гене-рального коэффициента корреляции при конкурирующей гипотезе Н1: rг ≠ 0. Таким образом, при принятии нулевой гипотезы Х и Y некоррелированы, то есть не связаны линейной зависимостью, а при отклонении Н0 они коррелированы. В качестве критерия примем случайную величину
которая при справедливости нулевой гипотезы имеет распределение Стьюдент с k = n – 2 степенями свободы. Из вида конкурирующей гипотезы следует, что критическая область двусторонняя с границами ± tкр, где значение tкр(α, k) находится из таблиц для двусторонней критической области. Вычислив наблюдаемое значение критерия
и сравнив его с tкр, делаем вывод: - если |Tнабл| < tкр – нулевая гипотеза принимается (корреляции нет); - если |Tнабл| > tкр – нулевая гипотеза отвергается (корреляция есть).
Ранговая корреляция. Пусть объекты генеральной совокупности обладают двумя качественными признаками (то есть признаками, которые невозможно измерить точно, но которые позволяют сравнивать объекты между собой и располагать их в порядке убывания или возрастания качества). Договоримся для определенности располагать объекты в порядке ухудшения качества. Пусть выборка объема п содержит независимые объекты, обладающие двумя качествен-ными признаками: А и В. Требуется выяснить степень их связи между собой, то есть установить наличие или отсутствие ранговой корреляции. Расположим объекты выборки в порядке ухудшения качества по признаку А, предполагая, что все они имеют различное качество по обоим признакам. Назовем место, занимаемое в этом ряду некоторым объектом, его рангом хi: х1 = 1, х2 = 2,…, хп = п.
Теперь расположим объекты в порядке ухудшения качества по признаку В, присвоив им ранги уi, где номер i равен порядковому номеру объекта по признаку А, а само значение ранга равно порядковому номеру объекта по признаку В. Таким образом, получены две последовательности рангов: по признаку А … х1, х2,…, хп по признаку В … у1, у2,…, уп. При этом, если, например, у3 = 6, то это означает, что данный объект занимает в ряду по признаку А третье место, а в ряду по признаку В – шестое. Сравним полученные последовательности рангов. Если xi = yi при всех значениях i, то ухудшение качества по признаку А влечет за собой ухудшение качества по признаку В, то есть имеется «полная ранговая зависимость». Если ранги противоположны, то есть х1 = 1, у1 = п; х2 = 2, у2 = п – 1;…, хп = п, уп = 1, то признаки тоже связаны: ухудшение качества по одному из них приводит к улучшению качества по другому («противоположная зависимость»). На практике чаще всего встречается промежуточный случай, когда ряд уi не монотонен. Для оценки связи между признаками будем считать ранги х1, х2,…, хп возможными значениями случайной величины Х, а у1, у2,…, уп – возможными значениями случайной величины Y. Теперь можно исследовать связь между Х и Y, вычислив для них выборочный коэффициент корреляции
где
Итак, требуется найти Можно показать, что
|
|||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.78.148 (0.009 с.) |

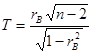 , (12.1)
, (12.1)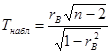
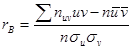 , (12.2)
, (12.2)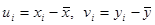 (условные варианты). Поскольку каждому рангу xi соответствует только одно значение yi, то частота любой пары условных вариант с одинаковыми индексами равна 1, а с разными индексами – нулю. Кроме того, из выбора условных вариант следует, что
(условные варианты). Поскольку каждому рангу xi соответствует только одно значение yi, то частота любой пары условных вариант с одинаковыми индексами равна 1, а с разными индексами – нулю. Кроме того, из выбора условных вариант следует, что  , поэтому формула (21.2) приобретает более простой вид:
, поэтому формула (21.2) приобретает более простой вид: . (12.3)
. (12.3)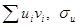 и
и  .
. . Учитывая, что
. Учитывая, что 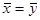 , можно выразить
, можно выразить 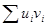 через разности рангов
через разности рангов 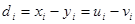 . После преобразований получим:
. После преобразований получим:  ,
, 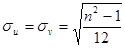 , откуда
, откуда 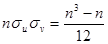 . Подставив эти результаты в (21.3), получим выборочный коэффициент ранговой корреляции Спирмена:
. Подставив эти результаты в (21.3), получим выборочный коэффициент ранговой корреляции Спирмена: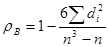 . (12.4)
. (12.4)


