
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии для проверки гипотезыСодержание книги
Поиск на нашем сайте
1. Критерий для проверки гипотезы о вероятности события. Пусть проведено п независимых испытаний (п – достаточно большое число), в каждом из которых некоторое событие А появляется с одной и той же, но неизвестной вероятностью р, и найдена относительная частота Примем в качестве статистического критерия случайную величину
имеющую нормальное распределение с параметрами M(U) = 0, σ(U) = 1 (то есть нормированную). Здесь q0 = 1 – p0. Вывод о нормальном распределении критерия следует из теоремы Лапласа (при достаточно большом п относительную частоту можно приближенно считать нормально распределенной с математическим ожиданием р и средним квадратическим отклонением Критическая область строится в зависимости от вида конкурирующей гипотезы. 1) Если Н0: р = р0, а Н1: р ≠ р0, то критическую область нужно построить так, чтобы вероятность попадания критерия в эту область равнялась заданному уровню значимости α. При этом наибольшая мощность критерия достигается тогда, когда критическая область состоит из двух интервалов, вероятность попадания в каждый из которых равна
Замечание. Предполагается, что используется таблица значений функции Лапласа, заданной в виде
Далее нужно вычислить наблюдаемое значение критерия:
Если |Uнабл| < uкр, то нулевая гипотеза принимается. Если |Uнабл| > uкр, то нулевая гипотеза отвергается. 2) Если конкурирующая гипотеза Н1: р > p0, то критическая область определяется неравенством U > uкр, то есть является правосторонней, причем р(U > uкр) = α. Тогда Если Uнабл < uкр, то нулевая гипотеза принимается. Если Uнабл > uкр, то нулевая гипотеза отвергается. 3) Для конкурирующей гипотезы Н1: р < p0 критическая область является левосторонней и задается неравенством U <- uкр, где uкр вычисляется так же, как в предыдущем случае. Если Uнабл > - uкр, то нулевая гипотеза принимается. Если Uнабл < - uкр, то нулевая гипотеза отвергается.
Пример. Пусть проведено 50 независимых испытаний, и относительная частота появления события А оказалась равной 0,12. Проверим при уровне значимости α = 0,01 нулевую гипотезу Н0: р = 0,1 при конкурирующей гипотезе Н1: р > 0,1. Найдем
2. Критерий для проверки гипотезы о математическом ожидании.
Пусть генеральная совокупность Х имеет нормальное распределение, и требуется проверить предположение о том, что ее математическое ожидание равно некоторому числу а0. Рассмотрим две возможности. 1) Известна дисперсия σ2 генеральной совокупности. Тогда по выборке объема п найдем выборочное среднее Учитывая, что выборочное среднее
Это случайная величина, имеющая нормальное распределение, причем, если нулевая гипотеза справедлива, то М(U) = 0, σ(U) = 1. Выберем критическую область в зависимости от вида конкурирующей гипотезы: ü если Н1: М( ü если Н1: М( ü если Н1: М(
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.232 (0.007 с.) |

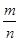 появлений А в этой серии испытаний. Проверим при заданном уровне значимости α нулевую гипотезу Н0, состоящую в том, что вероятность р равна некоторому значению р0.
появлений А в этой серии испытаний. Проверим при заданном уровне значимости α нулевую гипотезу Н0, состоящую в том, что вероятность р равна некоторому значению р0. , (11.1)
, (11.1)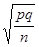 ).
). . Поскольку U симметрична относительно оси Оу, вероятность ее попадания в интервалы (-∞; 0) и (0; +∞) равна 0,5, следовательно, критическая область тоже должна быть симметрична относительно Оу. Поэтому икр определяется по таблице значений функции Лапласа из условия
. Поскольку U симметрична относительно оси Оу, вероятность ее попадания в интервалы (-∞; 0) и (0; +∞) равна 0,5, следовательно, критическая область тоже должна быть симметрична относительно Оу. Поэтому икр определяется по таблице значений функции Лапласа из условия 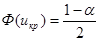 , а критическая область имеет вид
, а критическая область имеет вид 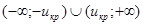 .
. , где нижний предел интегрирования равен 0, а не -∞. Функция Лапласа, заданная таким образом, является нечетной, а ее значения на 0,5 меньше, чем значения стандартной функции Ф(х) (см. лекцию 6).
, где нижний предел интегрирования равен 0, а не -∞. Функция Лапласа, заданная таким образом, является нечетной, а ее значения на 0,5 меньше, чем значения стандартной функции Ф(х) (см. лекцию 6).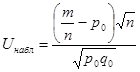 . (11.2)
. (11.2)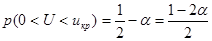 . Следовательно, икр можно найти по таблице значений функции Лапласа из условия, что
. Следовательно, икр можно найти по таблице значений функции Лапласа из условия, что 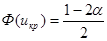 . Вычислим наблюдаемое значение критерия по формуле (19.2).
. Вычислим наблюдаемое значение критерия по формуле (19.2).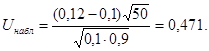 Критическая область является правосторонней, а икр находим из равенства Ф(uкр) =
Критическая область является правосторонней, а икр находим из равенства Ф(uкр) =  Из таблицы значений функции Лапласа определяем uкр = 2,33. Итак, Uнабл < uкр, и гипотеза о том, что р = 0,1, принимается.
Из таблицы значений функции Лапласа определяем uкр = 2,33. Итак, Uнабл < uкр, и гипотеза о том, что р = 0,1, принимается. и проверим нулевую гипотезу Н0: М(Х) = а0.
и проверим нулевую гипотезу Н0: М(Х) = а0. является несмещенной оценкой М(Х), то есть М(
является несмещенной оценкой М(Х), то есть М(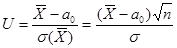 . (11.3)
. (11.3) , и, если |Uнабл| < uкр, то нулевая гипотеза принимается; если |Uнабл| > uкр, то нулевая гипотеза отвергается.
, и, если |Uнабл| < uкр, то нулевая гипотеза принимается; если |Uнабл| > uкр, то нулевая гипотеза отвергается.


