
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценокСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть требуется изучить некоторый количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак и необходимо оценить параметры, которыми оно определяется. Например, если изучаемый признак распределен в генеральной совокупности нормально, то нужно оценить математическое ожидание и среднее квадратическое отклонение; если признак имеет распределение Пуассона – то необходимо оценить параметр l. Обычно имеются лишь данные выборки, например значения количественного признака
Для того чтобы статистические оценки давали корректные приближения оцениваемых параметров, они должны удовлетворять некоторым требованиям, среди которых важнейшими являются требования несмещенности и состоятельности оценки. Пусть ά– статистическая оценка неизвестного параметра Если оценка άдает приближенное значение Аналогично, если άдает оценку с недостатком, то M(ά) < α. Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. Если, напротив, M(ά) = α, то это гарантирует от систематических ошибок.
Несмещенной называют статистическую оценку ά, математическое ожидание которой равно оцениваемому параметру Смещенной называют оценку, не удовлетворяющую этому условию. Несмещенность оценки еще не гарантирует получения хорошего приближения для оцениваемого параметра, так как возможные значения Эффективной называют статистическую оценку, которая, при заданном объеме выборки n, имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности. Состоятельной называется статистическая оценка, которая при n®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n®¥ стремится к нулю, то такая оценка оказывается и состоятельной. Надежность и доверительный интервал До сих пор мы рассматривали точечные оценки, т.е. такие оценки, которые определяются одним числом. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. В связи с этим при небольшом объеме выборки пользуются интервальными оценками. Интервальной называют оценку, определяющуюся двумя числами – концами интервала. Пусть найденная по данным выборки статистическая характеристика άслужит оценкой неизвестного параметра α. Очевидно, άтем точнее определяет параметр Статистические методы не позволяют утверждать, что оценка άудовлетворяет неравенству |α -ά|<δ, можно говорить лишь о вероятности, с которой это неравенство осуществляется. Надежностью (доверительной вероятностью) оценки αпо ά называют вероятность g, с которой осуществляется неравенство |α - ά| < δ. Обычно надежность оценки задается заранее, причем, в качестве g берут число, близкое к единице – как правило, 0,95; 0,99 или 0,999.
Пусть вероятность того, что |α - ά| < δ равна g:
Заменим неравенство Это соотношение следует понимать так: вероятность того, что интервал Таким образом, доверительным называют интервал Статистическая гипотеза. Определение 11.1. Статистической гипотезой называют гипотезу о виде неизвестного распределения генеральной совокупности или о параметрах известных распределений. Определение 11.2. Нулевой (основной) называют выдвинутую гипотезу Н0. Конкурирую-щей (альтернативной) называют гипотезу Н1, которая противоречит нулевой. Пример. Пусть Н0 заключается в том, что математическое ожидание генеральной совокупности а = 3. Тогда возможные варианты Н1: а) а ≠ 3; б) а > 3; в) а < 3. Определение 11.3. Простой называют гипотезу, содержащую только одно предположение, сложной – гипотезу, состоящую из конечного или бесконечного числа простых гипотез. Пример. Для показательного распределения гипотеза Н0: λ = 2 – простая, Н0: λ > 2 – сложная, состоящая из бесконечного числа простых (вида λ = с, где с – любое число, большее 2). В результате проверки правильности выдвинутой нулевой гипотезы (такая проверка называется статистической, так как производится с применением методов математической статистики) возможны ошибки двух видов: 1. ошибка первого рода, состоящая в том, что будет отвергнута правильная нулевая гипотеза; 2. ошибка второго рода, заключающаяся в том, что будет принята неверная гипотеза. Замечание. Какая из ошибок является на практике более опасной, зависит от конкретной задачи. Например, если проверяется правильность выбора метода лечения больного, то ошибка первого рода означает отказ от правильной методики, что может замедлить лечение, а ошибка второго рода (применение неправильной методики) чревата ухудшением состояния больного и является более опасной. Определение 11.4. Вероятность ошибки первого рода называется уровнем значимости α. Основной прием проверки статистических гипотез заключается в том, что по имеющейся выборке вычисляется значение некоторой случайной величины, имеющей известный закон распределения. Определение 11.5. Статистическим критерием называется случайная величина К с известным законом распределения, служащая для проверки нулевой гипотезы. Определение 11.6. Критической областью называют область значений критерия, при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают.
Процесс проверки гипотезы состоит из следующих этапов: 1. выбирается статистический критерий К; 2. вычисляется его наблюдаемое значение Кнабл по имеющейся выборке; 3. поскольку закон распределения К известен, определяется (по известному уровню значимости α) критическое значение kкр, разделяющее критическую область и область принятия гипотезы (например, если р(К > kкр) = α, то справа от kкр располагается критическая область, а слева – область принятия гипотезы); 4. если вычисленное значение Кнабл попадает в область принятия гипотезы, то нулевая гипотеза принимается, если в критическую область – нулевая гипотеза отвергается.
Различают разные виды критических областей: - правостороннюю критическую область, определяемую неравенством K > kкр (kкр > 0); - левостороннюю критическую область, определяемую неравенством K < kкр (kкр < 0); - двустороннюю критическую область, определяемую неравенствами K < k1, K > k2 (k2 > k1). Определение 11.7. Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что верна конкурирующая гипотеза. Если обозначить вероятность ошибки второго рода (принятия неправильной нулевой гипотезы) β, то мощность критерия равна 1 – β. Следовательно, чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода. Поэтому после выбора уровня значимости следует строить критическую область так, чтобы мощность критерия была максимальной.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 686; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.133.136 (0.008 с.) |

 , полученные в результате n независимых наблюдений. Рассматривая
, полученные в результате n независимых наблюдений. Рассматривая  можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая дает приближенное значение оцениваемого параметра. Например, для оценки математического ожидания нормального распределения роль функции выполняет среднее арифметическое:
можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая дает приближенное значение оцениваемого параметра. Например, для оценки математического ожидания нормального распределения роль функции выполняет среднее арифметическое:
 теоретического распределения. Пусть по выборке объема n найдена оценка
теоретического распределения. Пусть по выборке объема n найдена оценка 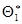 . Повторим опыт, т.е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным получим другую оценку ά2. Повторяя опыт многократно, получим различные числа. Оценку άможно рассматривать, как случайную величину, а числа ά1ά2ά3… άn– как ее возможные значения.
. Повторим опыт, т.е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным получим другую оценку ά2. Повторяя опыт многократно, получим различные числа. Оценку άможно рассматривать, как случайную величину, а числа ά1ά2ά3… άn– как ее возможные значения. могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия
могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия  может быть значительной. В этом случае найденная по данным одной выборки оценка, например
может быть значительной. В этом случае найденная по данным одной выборки оценка, например  , а значит, и от самого оцениваемого параметра.
, а значит, и от самого оцениваемого параметра. и |α -ά| < δ, то чем меньше d, тем точнее оценка. Таким образом, положительное число d характеризует точность оценки.
и |α -ά| < δ, то чем меньше d, тем точнее оценка. Таким образом, положительное число d характеризует точность оценки. .
.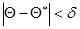 равносильным ему двойным неравенством
равносильным ему двойным неравенством  .
. заключает в себе (покрывает) неизвестный параметр Q, равна
заключает в себе (покрывает) неизвестный параметр Q, равна  .
.


